12 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Cho cấp số cộng có số hạng đầu \[{u_1} = 2\], công sai \[d = - 4\]. Số hạng thứ năm của cấp số cộng là
\[512\].
\[ - 14\].
\[ - 512\].
\[ - 18\].
Thống kê số phút học bài ở nhà mỗi ngày của \[100\] học sinh ta có bảng phân bố tần số ghép nhóm như sau
|
Số phút |
\[\left[ {30;60} \right)\] |
\[\left[ {60;90} \right)\] |
\[\left[ {90;120} \right)\] |
\[\left[ {120;150} \right)\] |
|
Số học sinh |
\[18\] |
\[15\] |
\[42\] |
\[25\] |
Số học sinh có thời gian học ít hơn \[2\] tiếng trong số học sinh trên là
\[15\].
\[33\].
\[75\].
\[18\].
Trong không gian với hệ tọa độ \[Oxyz\], cho điểm \[A\left( {1;2; - 1} \right)\]. Tọa độ hình chiếu vuông góc của \[A\] trên mặt phẳng \[\left( {Oyz} \right)\] là
\[\left( {0;2; - 1} \right)\].
\[\left( {1;0;0} \right)\].
\[\left( {1;2;0} \right)\].
\[\left( {1;0; - 1} \right)\].
Gọi \[M,m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[f\left( x \right) = {x^4} - 2{x^2} - 1\] trên đoạn \[\left[ { - 1;2} \right]\]. Giá trị của biểu thức \[M + 2m\] bằng
\[3\].
\[5\].
\[6\].
\[4\].
Cho khối lăng trụ đều có diện tích đáy bằng \[2\,\,({{\rm{m}}^{\rm{2}}})\] và chiều cao bằng \[3\,\,{\rm{(m)}}\]. Thể tích khối lăng trụ đã cho bằng
\[\frac{{3\sqrt 3 }}{2}\,({{\rm{m}}^3})\].
\[2\,({{\rm{m}}^3})\].
\[\frac{{\sqrt 3 }}{2}({{\rm{m}}^3})\].
\[6\,({{\rm{m}}^3})\].
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có bảng biến thiên như sau:
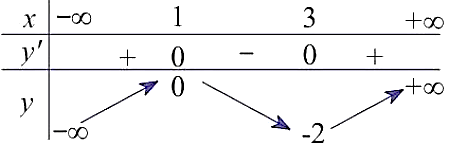
Hàm số đã cho nghịch biến trên khoảng
\[\left( { - 2;0} \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( {3; + \infty } \right)\].
\[\left( {1;3} \right)\].
Đường tiệm cận xiên của đồ thị hàm số \[y = 2x - 1 + \frac{1}{x}\] có phương trình là:
\[y = 1 - 2x\].
\[y = 2x\].
\[y = 2x - 1\].
\[y = - 2x\].
Hàm số nào dưới đây có đồ thị như hình vẽ sau?
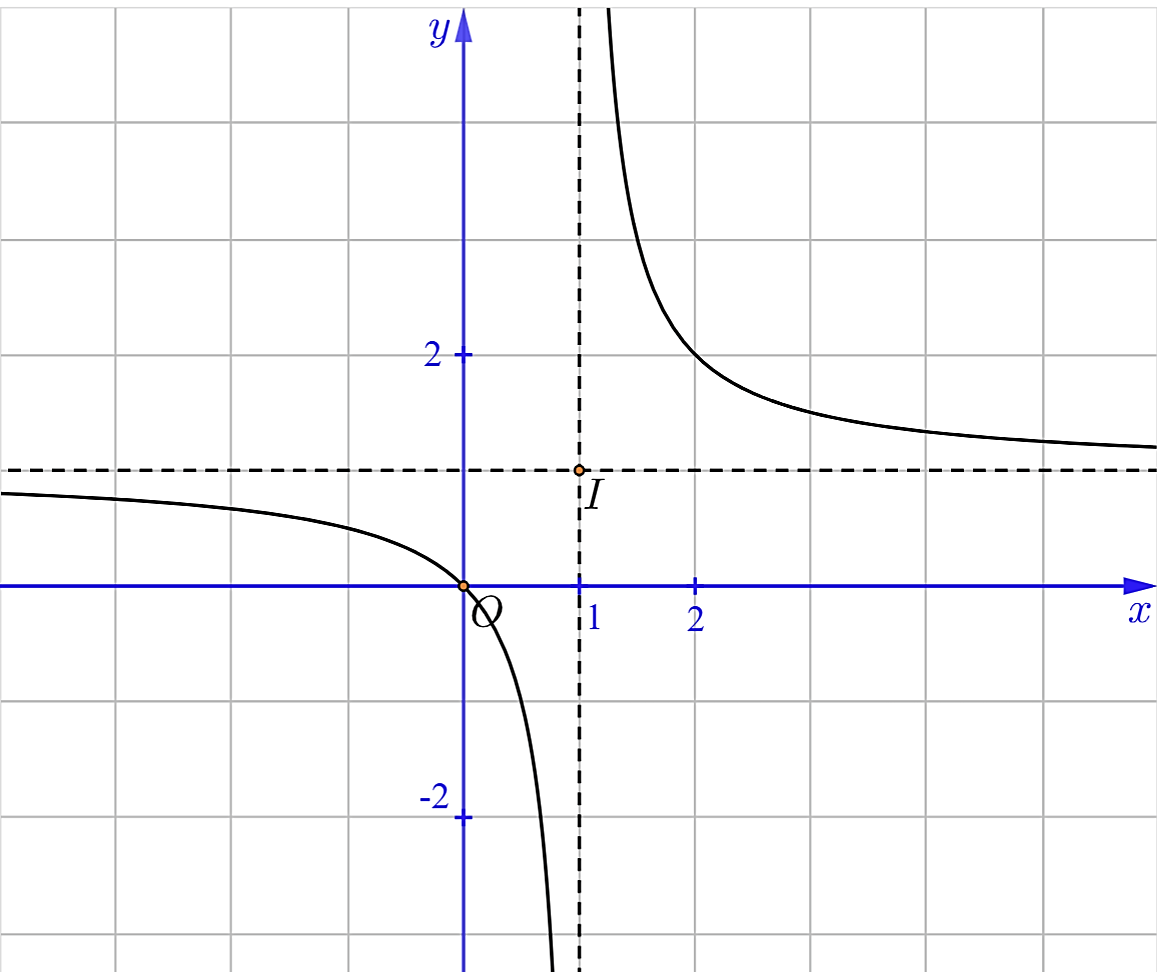
\[y = \frac{x}{{x + 1}}\].
\[y = - \frac{x}{{x - 1}}\].
\[y = - \frac{x}{{x + 1}}\].
\[y = \frac{x}{{x - 1}}\].
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới đây.
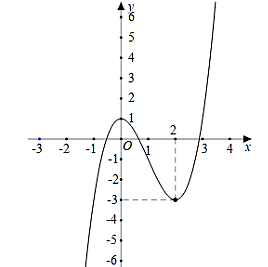
Giá trị cực tiểu của hàm số đã cho là
\( - 3\).
\(2\).
\(1\).
\(0\).
Tập nghiệm của bất phương trình \[{\log _{\frac{1}{3}}}\left( {x - 1} \right) > - 2\] là
\(\left( {10; + \infty } \right)\).
\(\left( {1;10} \right)\).
\(\left( {9; + \infty } \right)\).
\(\left( { - \infty ;10} \right)\).
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Đẳng thức nào sau đây là đẳng thức đúng?
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow 0 \).
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
\(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SC} + \overrightarrow {SD} \).
\(\overrightarrow {SB} + \overrightarrow {SC} = \overrightarrow {SA} + \overrightarrow {SD} \).
Cho \(A\) và \(B\) là hai biến cố độc lập. Biết xác suất của biến cố \(A\) là \(0,4\); xác suất của biến cố \(B\) là \(0,3\). Xác suất của biến cố \(A \cup B\) là
\(0,12\).
\(0,58\).
\(0,7\).
\(0,82\).
