Bộ 3 đề KSCL đầu năm Toán 11 có đáp án - Đề 3
21 câu hỏi
A. TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Số đo theo đơn vị rađian của góc \(315^\circ \) là:
\(\frac{{7\pi }}{4}\).
\(\frac{{4\pi }}{7}\).
\(\frac{{7\pi }}{2}\).
\(\frac{{2\pi }}{7}\).
Hàm số nào sau đây là hàm số bậc hai?
\(y = {x^3} - x + 2\).
\(y = {\left( {\frac{1}{x}} \right)^2} + 2 \cdot \frac{1}{x} + 2\).
\(y = {x^2} + x - 1\).
\(y = 0{x^2} + x - 1\).
Phương trình đường thẳng đi qua hai điểm \[A\left( {0;4} \right),B\left( { - 6;0} \right)\] là:
\[\frac{x}{6} + \frac{y}{4} = 1\].
\[\frac{{ - x}}{4} + \frac{y}{{ - 6}} = 1\].
\[\frac{{ - x}}{6} + \frac{y}{4} = 1\].
\[\frac{x}{4} + \frac{y}{{ - 6}} = 1\].
Tìm tọa độ giao điểm của hai đường thẳng \[7x - 3y + 16 = 0\] và \[x + 10 = 0\].
\[\left( { - 10; - 18} \right)\].
\[\left( {10;18} \right)\].
\[\left( { - 10;18} \right)\].
\[\left( {10; - 18} \right)\].
Trong mặt phẳng \[Oxy\], cho đường tròn \[\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\]. Đường tròn có tâm và bán kính là
\[I\left( { - 3;2} \right),\,\,R = 3\].
\[I\left( { - 2;3} \right),\,\,R = 3\].
\[I\left( {2;3} \right),\,\,R = 9\].
\[I\left( {2; - 3} \right),\,\,R = 3\].
Số tập hợp con có \[3\] phần tử của một tập hợp có \[7\] phần tử là
\[C_7^3\].
\[\frac{{7!}}{{3!}}\].
\[A_7^3\].
\[7\].
Cho hình chóp \(S.ABCD\) có \(AC \cap BD = O\) (như hình vẽ). Giao tuyến của mặt phẳng \(\left( {SAC} \right)\) và mặt phẳng \(\left( {SBD} \right)\) là đường thẳng nào sau đây?
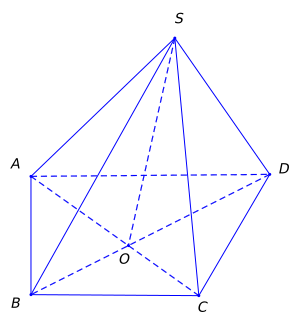
\(SA.\)
\(SC.\)
\(SB.\)
\(SO.\)
Cho biết \(\sin \alpha \cdot \cos \alpha = - \,\frac{1}{4}\) thì \({\tan ^2}\alpha + {\cot ^2}\alpha \) bằng.
12.
14.
16.
18.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang, \[AD\,{\rm{//}}\,BC\], \[AD = 2BC\]. \(M\) là trung điểm của \(SA\). Mặt phẳng \(\left( {MBC} \right)\) cắt \[SD\] tại \(N\). Khi đó tứ giác \(BCNM\) là hình gì?
Hình bình hành.
Tam giác.
Hình chữ nhật.
Hình thang.
Cho \(\cos \alpha = \frac{1}{3}\). Khi đó \(\sin \left( {\alpha - \frac{{3\pi }}{2}} \right)\) bằng
\( - \frac{1}{3}.\)
\(\frac{2}{3}.\)
\( - \frac{2}{3}.\)
\(\frac{1}{3}.\)
Hệ số của \({x^4}\) trong khai triển \({\left( {2x - 1} \right)^5}\) là
\( - 80\).
\(80\).
\( - 40\).
\(40\).
Cho \(\cos x = \frac{1}{3}\left( { - \frac{\pi }{2} < x < 0} \right)\). Giá trị của \(\tan 2x\) là
</>
\(\frac{{4\sqrt 2 }}{7}\).
\(\frac{{\sqrt 5 }}{2}\).
\( - \frac{{4\sqrt 2 }}{7}\).
\( - \frac{{\sqrt 5 }}{2}\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Một tấm sắt hình chữ nhật có chu vi là 96 cm. Người ta cắt ở mỗi góc tấm sắt một hình vuông cạnh là 4 cm.
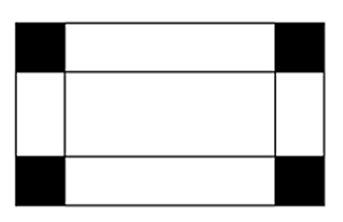
a) Diện tích phần cắt đi là \[4 \cdot {4^2}\]\[\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
b) Gọi chiều dài của tấm sắt là \[x\] (cm) thì chiều rộng tấm sắt là \[96 - x\] (cm).
c) Diện tích phần còn lại của tấm sắt là \[ - {x^2} + 48x - 64\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
d)Diện tích phần còn lại của tấm sắt ít nhất bằng 448 \({\rm{c}}{{\rm{m}}^{\rm{2}}}\) khi và chỉ khi chiều dài của tấm sắt nằm trong đoạn \[\left[ {16;32} \right]\] (cm).
Cho hình bình hành \(ABCD\) và một điểm \(S\) không thuộc mặt phẳng \(\left( {ABCD} \right)\), các điểm \(M,N\) lần lượt là trung điểm của đoạn thẳng \(AB,SC\). Gọi \(O = AC \cap BD\).
a)\(SO\) giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\).
b) Giao điểm của \(I\) của đường thẳng \(AN\) và mặt phẳng \(\left( {SBD} \right)\) là điểm nằm trên đường thẳng \(SO\).
c) Giao điểm của \(J\) của đường thẳng \(MN\) và mặt phẳng \(\left( {SBD} \right)\) là điểm nằm trên đường thẳng \(SD\).
d) Ba điểm \(I,J,B\) thẳng hàng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Trong kỳ thi học sinh giỏi cấp tỉnh vừa qua có \(9\) học sinh đạt giải cao, trong đó khối xã hội có \(4\)nữ và \(1\)nam, khối tự nhiên có \(1\)nữ và \(3\)nam. Có bao nhiêu cách chọn ra \(5\)học sinh để trao học bổng biết rằng \(5\)học sinh này vừa có khối tự nhiên, vừa có khối xã hội, vừa có nam, vừa có nữ và số học sinh nam ít hơn số học sinh nữ?
Một vật chuyển động có vận tốc \({\rm{(m/s)}}\) được biểu diễn theo thời gian \(t\,(\;{\rm{s}})\) bằng công thức \(v\left( t \right) = \frac{1}{2}{t^2} - 4t + 10\). Vận tốc của vật đạt giá trị nhỏ nhất bằng bao nhiêu?
Cho tam giác đều \(ABC\) có độ dài cạnh bằng 6. Lấy điểm \(M\) trên cạnh \(BC\) sao cho \(MB = 2MC\). Tính tích vô hướng của hai vectơ \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \).
Thầy Khánh có 5 quyển sách toán, 6 quyển sách lý và 4 quyển sách hóa. Các quyển sách đôi một khác nhau. Thầy Khánh chọn ngẫu nhiên 7 quyển sách để làm phần thưởng cho một học sinh giỏi. Tính xác suất để số quyển sách còn lại của Thầy Khánh có đủ 3 môn học (làm tròn kết quả đến hàng phần trăm).
B. TỰ LUẬN
Trong mặt phẳng\(Oxy\), cho hai điểm \(A\left( {1;2} \right)\); \(B\left( { - 5;3} \right)\) và đường thẳng \(\Delta :\,3x - 4y + 7 = 0\).
a) Viết phương trình đường thẳng \(d\) đi qua hai điểm\(A\)và \(B\).
b) Viết phương trình đường tròn \(\left( C \right)\) có tâm \(B\)và tiếp xúc với đường thẳng \(\Delta \).
Cho \(\cos \alpha = \frac{2}{3}\), \(\left( {0\, < \alpha \, < \,\frac{\pi }{2}} \right)\).
a) Tính giá trị của biểu thức \(P = \left( {1 - \sin \alpha } \right)\left( {1 + \sin \alpha } \right)\).
b) Tính \(\cos \left( {\frac{\pi }{3} - 2\alpha } \right)\).
Một xưởng sản xuất bàn và ghế. Một chiếc bàn cần 1,5 giờ lắp ráp và 1 giờ hoàn thiện. Một chiếc ghế cần 1 giờ lắp ráp và 2 giờ hoàn thiện. Bộ phận lắp ráp có 3 công nhân, bộ phận hoàn thiện có 4 công nhân. Mỗi công nhân không làm việc quá 8 giờ một ngày và năng suất lao động của công nhân ở mỗi bộ phận đều như nhau. Thị trường luôn tiêu thụ hết sản phẩm của xưởng và lượng ghế tiêu thụ không vượt quá 3,5 lần số bàn. Một chiếc bàn lãi 600 nghìn đồng, một chiếc ghế lãi 450 nghìn đồng.Hỏi trong một ngày, xưởng sản xuất cần sản xuất bao nhiêu chiếc bàn và chiếc ghế để thu được tiền lãi cao nhất?


