Bộ 3 đề KSCL đầu năm Toán 11 có đáp án - Đề 2
21 câu hỏi
A. TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Parabol \(\left( P \right):y = {x^2} - 4x + 5\) có phương trình trục đối xứng là:
\(x = - 1\).
\(x = - 2\).
\(x = 1\).
\(x = 2\).
Cho tam thức bậc hai \(f\left( x \right) = {x^2} + x + 1\). Mệnh đề nào sau đây đúng?
\(f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ; + \infty } \right)\).
\(f\left( x \right) = 0 \Leftrightarrow x = - 1\).
\(f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \infty ;1} \right)\).
\(f\left( x \right) > 0 \Leftrightarrow x \in \left( {0;1} \right)\).
Trong mặt phẳng \(\left( {Oxy} \right)\), cho đường thẳng \(\Delta \) đi qua điểm \(M\left( { - 8;6} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 1} \right)\). Viết phương trình tham số của đường thẳng \(\Delta \).
\(\left\{ {\begin{array}{*{20}{l}}{x = - 8 + t}\\{y = 6 + 2t}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{x = 4 + 2t}\\{y = - 4 - t}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{x = 2 - 8t}\\{y = - 1 + 6t}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{x = - 8 + 2t}\\{y = 6 - t}\end{array}} \right.\).
Khoảng cách từ điểm \(M\left( {3; - 1} \right)\) đến đường thẳng \(\Delta :2x - y + 5 = 0\) nằm trong khoảng nào sau đây?
\[\left( {1;3} \right)\].
\(\left( {3;5} \right)\).
\(\left( {7;9} \right)\).
\(\left( {5;7} \right)\).
Viết phương trình đường tròn \(\left( C \right)\) có đường kính \(AB\) với \(A\left( {1;2} \right),B\left( {3;0} \right)\).
\(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = \sqrt 2 \).
\(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 2\).
\(\left( C \right):{\left( {x - 2} \right)^2} + {y^2} = \sqrt 2 \).
\(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y + 2} \right)^2} = 2\).
Cho góc \[\alpha \] thoả mãn \[90^\circ < \alpha < 180^\circ \]. Trong các khẳng định sau, khẳng định nào đúng?
\[\tan \alpha < 0\].
\[cos\alpha \ge 0\].
\[cot\alpha > 0\].
\[\sin \alpha < 0\].
Rút gọn biểu thức \(A = \frac{{\sin 3x + \cos 2x - \sin x}}{{\cos x + \sin 2x - \cos 3x}}\left( {\sin 2x \ne 0;2\sin x + 1 \ne 0} \right)\) ta được:
\(A = \cot 3x\).
\(A = \cot 6x\).
\(A = \tan x + \tan 2x + \tan 3x\).
\(A = \cot 2x\).
Cho bốn điểm \(A,B,C,D\) không cùng nằm trong một mặt phẳng. Trên \(AB,AD\) lần lượt lấy các điểm \(M\) và \[N\] sao cho \(MN\) cắt \(BD\) tại \(I\) (Hình vẽ dưới đây). Điểm \(I\) không thuộc mặt phẳng nào sau đây?
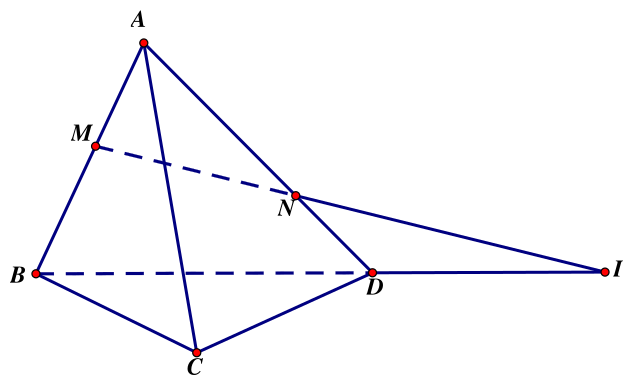
\(\left( {BCD} \right)\).
\(\left( {ABD} \right)\).
\(\left( {CMN} \right)\).
\(\left( {ACD} \right)\).
Cho tập hợp \(S = \left\{ {1;2;3;4;5;6} \right\}\). Có thể lập được bao nhiêu số tự nhiên gồm bốn chữ số khác nhau lấy từ tập hợp \(S\)?
\(360\).
\(120\).
\(15\).
\(20\).
Cho \[\cos \alpha = - \frac{2}{3}\], \[\cos 2\alpha \] nhận giá trị nào trong các giá trị sau?
\( - \frac{2}{3}\).
\( - \frac{4}{3}\).
\( - \frac{1}{9}\).
\(\frac{4}{3}\).
Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất bốn lần. Xác suất để cả bốn lần gieo đều xuất hiện mặt sấp là
\(\frac{4}{{16}}\).
\(\frac{2}{{16}}\).
\(\frac{1}{{16}}\).
\(\frac{6}{{16}}\).
Cho hình chóp\(S.ABCD\) có đáy \(ABCD\) là hình thang \(\left( {AB{\rm{//}}CD} \right)\). Gọi \(M\), \(N\) và \(P\) lần lượt là trung điểm của \(BC\), \(AD\) và \(SA\). Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {MNP} \right)\) là
Đường thẳng \(PM\).
Đường thẳng qua \(S\) và song song với \(AB\).
Đường thẳng qua \(M\) và song song với \(SC\).
Đường thẳng qua \(P\) và song song với \(AB\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Cho đường tròn \(\left( C \right)\) có phương trình \({x^2} + {y^2} - 6x + 2y + 6 = 0\) và điểm \(A\left( {1; - 1} \right)\).
a) Điểm \(A\)thuộc đường tròn.
b) Đường tròn có tâm \[I\left( {3;1} \right)\].
c) Đường tròn có bán kính \(R = 2\).
d) Phương trình tiếp tuyến của đường tròn tại điểm \(A\)là: \(x - 1 = 0\).
Cho \(\cos x = - \frac{5}{{13}}\) với \(180^\circ < x < 270^\circ \).
a)\(\sin x < 0\).
b)\(\tan x = \frac{{12}}{5}\).
c)\(\cot x = \frac{5}{{12}}\).
d)\(\sin x - \cos x = - \frac{{12}}{{13}}\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Có bao nhiêu số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các chữ số \(0,1,2,3,4,5,6\)?
Có hai con tàu \(A,B\) xuất phát từ hai bến, chuyển động theo đường thẳng ngoài biển. Trên màn hình ra-đa của trạm điều khiển (xem như mặt phẳng tọa độ \(Oxy\) với đơn vị trên các trục tính bằng ki-lô-mét), tại thời điểm \(t\) (giờ), vị trí của tàu \(A\) có tọa độ được xác định bởi công thức \(\left\{ {\begin{array}{*{20}{l}}{x = 3 - 33t}\\{y = - 4 + 25t}\end{array}} \right.\); vị trí tàu \(B\) có tọa độ là \(\left( {4 - 30t;3 - 40t} \right)\). Nếu tàu \(A\) đứng yên ở vị trí ban đầu, tàu \(B\) chạy thì khoảng cách ngắn nhất giữa hai tàu bằng bao nhiêu ki-lô-mét?
Biểu thức \(T = 2\sin \left( {\frac{{9\pi }}{2} - x} \right) + 3\cos \left( {19\pi - x} \right) = k\cos x\) . Khi đó \(k = ?\)
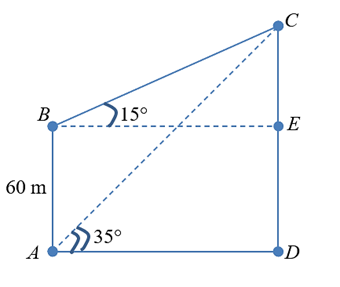
Một người quan sát đỉnh Ccủa một ngọn núi từ hai vị trí khác nhau của tòa nhà (tham khảo hình vẽ). Lần đầu tiên, người đó quan sát đỉnh núi từ tầng trệt Avới phương nhìn tạo với phương nằm ngang góc \(35^\circ \). Lần thứ hai, người này quan sát tại sân thượng Bcủa cùng tòa nhà đó, với phương nhìn tạo với phương nằm ngang góc\(15^\circ \). Biết rằng tòa nhà cao \(60\,{\rm{m}}\), tính chiều cao CD của ngọn núi (làm tròn kết quả đến hàng đơn vị của mét).
B. TỰ LUẬN
Một đường dây điện được nối từ nhà máy điện trên đất liền ở vị trí\(A\)đến một hòn đảo ở vị trí\(D\). Khoảng cách ngắn nhất từ\(D\)vào đất liền là\(DC = 2\,{\rm{km}}\). Khoảng cách từ\(A\)đến \(C\)là\(5\,{\rm{km}}\). Người ta chọn một vị trí (điểm\(B\)) nằm giữa\(A\)và \(C\)để mắc đường dây điện từ \(A\)đến \(B\), rồi từ \(B\)đến\(D\).Chi phí mắc mỗikilômétdây điện trên đất liền là \(3000\,{\rm{USD}}\), chi phí mắc mỗi kilômétdây điện ngầm dưới biển là \(5000\,{\rm{USD}}\). Hỏi điểm\(B\)phải cách điểm\(A\)bao nhiêu kilômét, biết tổng chi phí mắc dây điện nối từ vị trí \(A\) đến vị trí \(D\) theo cách trên là \(23000\,{\rm{USD}}\).
Một hộp chứa \[20\]cái thẻ được đánh số từ \(1\) đến \(20\) (mỗi thẻ đánh một số). Rút ngẫu nhiên đồng thời \(2\) thẻ. Tính xác suất để rút được hai thẻ mà tổng hai số ghi trên thẻ là một số lẻ.
Cho hình chóp \(S.ABC.\) Gọi\(M,P\) lần lượt thuộc các cạnh \(SA,AB\) sao cho \(MA = 2MS;BP = 2PA\) và \(N\)là trung điểm của \(BC\).
a) Tìm giao điểm \(K\) của \(SC\) và mặt phẳng \(\left( {MNP} \right).\)
b) Chứng minh \(MK,PN,AC\) đồng quy.


