12 câu hỏi
A. TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Số đo theo đơn vị rađian của góc \(315^\circ \) là:
\(\frac{{7\pi }}{4}\).
\(\frac{{4\pi }}{7}\).
\(\frac{{7\pi }}{2}\).
\(\frac{{2\pi }}{7}\).
Hàm số nào sau đây là hàm số bậc hai?
\(y = {x^3} - x + 2\).
\(y = {\left( {\frac{1}{x}} \right)^2} + 2 \cdot \frac{1}{x} + 2\).
\(y = {x^2} + x - 1\).
\(y = 0{x^2} + x - 1\).
Phương trình đường thẳng đi qua hai điểm \[A\left( {0;4} \right),B\left( { - 6;0} \right)\] là:
\[\frac{x}{6} + \frac{y}{4} = 1\].
\[\frac{{ - x}}{4} + \frac{y}{{ - 6}} = 1\].
\[\frac{{ - x}}{6} + \frac{y}{4} = 1\].
\[\frac{x}{4} + \frac{y}{{ - 6}} = 1\].
Tìm tọa độ giao điểm của hai đường thẳng \[7x - 3y + 16 = 0\] và \[x + 10 = 0\].
\[\left( { - 10; - 18} \right)\].
\[\left( {10;18} \right)\].
\[\left( { - 10;18} \right)\].
\[\left( {10; - 18} \right)\].
Trong mặt phẳng \[Oxy\], cho đường tròn \[\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\]. Đường tròn có tâm và bán kính là
\[I\left( { - 3;2} \right),\,\,R = 3\].
\[I\left( { - 2;3} \right),\,\,R = 3\].
\[I\left( {2;3} \right),\,\,R = 9\].
\[I\left( {2; - 3} \right),\,\,R = 3\].
Số tập hợp con có \[3\] phần tử của một tập hợp có \[7\] phần tử là
\[C_7^3\].
\[\frac{{7!}}{{3!}}\].
\[A_7^3\].
\[7\].
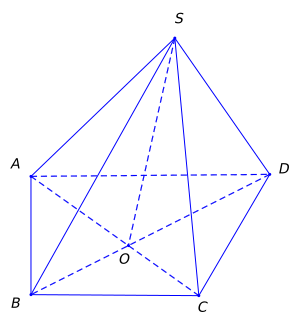
Cho hình chóp \(S.ABCD\) có \(AC \cap BD = O\) (như hình vẽ). Giao tuyến của mặt phẳng \(\left( {SAC} \right)\) và mặt phẳng \(\left( {SBD} \right)\) là đường thẳng nào sau đây?
\(SA.\)
\(SC.\)
\(SB.\)
\(SO.\)
Cho biết \(\sin \alpha \cdot \cos \alpha = - \,\frac{1}{4}\) thì \({\tan ^2}\alpha + {\cot ^2}\alpha \) bằng.
12.
14.
16.
18.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang, \[AD\,{\rm{//}}\,BC\], \[AD = 2BC\]. \(M\) là trung điểm của \(SA\). Mặt phẳng \(\left( {MBC} \right)\) cắt \[SD\] tại \(N\). Khi đó tứ giác \(BCNM\) là hình gì?
Hình bình hành.
Tam giác.
Hình chữ nhật.
Hình thang.
Cho \(\cos \alpha = \frac{1}{3}\). Khi đó \(\sin \left( {\alpha - \frac{{3\pi }}{2}} \right)\) bằng
\( - \frac{1}{3}.\)
\(\frac{2}{3}.\)
\( - \frac{2}{3}.\)
\(\frac{1}{3}.\)
Hệ số của \({x^4}\) trong khai triển \({\left( {2x - 1} \right)^5}\) là
\( - 80\).
\(80\).
\( - 40\).
\(40\).
Cho \(\cos x = \frac{1}{3}\left( { - \frac{\pi }{2} < x < 0} \right)\). Giá trị của \(\tan 2x\) là
</>
\(\frac{{4\sqrt 2 }}{7}\).
\(\frac{{\sqrt 5 }}{2}\).
\( - \frac{{4\sqrt 2 }}{7}\).
\( - \frac{{\sqrt 5 }}{2}\).
Gợi ý cho bạn
Xem tất cảBộ 3 đề KSCL đầu năm Toán 11 có đáp án - Đề 2