12 câu hỏi
A. TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Parabol \(\left( P \right):y = {x^2} - 4x + 5\) có phương trình trục đối xứng là:
\(x = - 1\).
\(x = - 2\).
\(x = 1\).
\(x = 2\).
Cho tam thức bậc hai \(f\left( x \right) = {x^2} + x + 1\). Mệnh đề nào sau đây đúng?
\(f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ; + \infty } \right)\).
\(f\left( x \right) = 0 \Leftrightarrow x = - 1\).
\(f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \infty ;1} \right)\).
\(f\left( x \right) > 0 \Leftrightarrow x \in \left( {0;1} \right)\).
Trong mặt phẳng \(\left( {Oxy} \right)\), cho đường thẳng \(\Delta \) đi qua điểm \(M\left( { - 8;6} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 1} \right)\). Viết phương trình tham số của đường thẳng \(\Delta \).
\(\left\{ {\begin{array}{*{20}{l}}{x = - 8 + t}\\{y = 6 + 2t}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{x = 4 + 2t}\\{y = - 4 - t}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{x = 2 - 8t}\\{y = - 1 + 6t}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{x = - 8 + 2t}\\{y = 6 - t}\end{array}} \right.\).
Khoảng cách từ điểm \(M\left( {3; - 1} \right)\) đến đường thẳng \(\Delta :2x - y + 5 = 0\) nằm trong khoảng nào sau đây?
\[\left( {1;3} \right)\].
\(\left( {3;5} \right)\).
\(\left( {7;9} \right)\).
\(\left( {5;7} \right)\).
Viết phương trình đường tròn \(\left( C \right)\) có đường kính \(AB\) với \(A\left( {1;2} \right),B\left( {3;0} \right)\).
\(\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = \sqrt 2 \).
\(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 2\).
\(\left( C \right):{\left( {x - 2} \right)^2} + {y^2} = \sqrt 2 \).
\(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y + 2} \right)^2} = 2\).
Cho góc \[\alpha \] thoả mãn \[90^\circ < \alpha < 180^\circ \]. Trong các khẳng định sau, khẳng định nào đúng?
\[\tan \alpha < 0\].
\[cos\alpha \ge 0\].
\[cot\alpha > 0\].
\[\sin \alpha < 0\].
Rút gọn biểu thức \(A = \frac{{\sin 3x + \cos 2x - \sin x}}{{\cos x + \sin 2x - \cos 3x}}\left( {\sin 2x \ne 0;2\sin x + 1 \ne 0} \right)\) ta được:
\(A = \cot 3x\).
\(A = \cot 6x\).
\(A = \tan x + \tan 2x + \tan 3x\).
\(A = \cot 2x\).
Cho bốn điểm \(A,B,C,D\) không cùng nằm trong một mặt phẳng. Trên \(AB,AD\) lần lượt lấy các điểm \(M\) và \[N\] sao cho \(MN\) cắt \(BD\) tại \(I\) (Hình vẽ dưới đây). Điểm \(I\) không thuộc mặt phẳng nào sau đây?
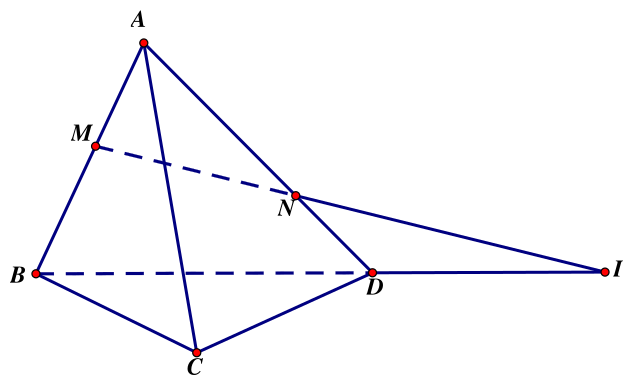
\(\left( {BCD} \right)\).
\(\left( {ABD} \right)\).
\(\left( {CMN} \right)\).
\(\left( {ACD} \right)\).
Cho tập hợp \(S = \left\{ {1;2;3;4;5;6} \right\}\). Có thể lập được bao nhiêu số tự nhiên gồm bốn chữ số khác nhau lấy từ tập hợp \(S\)?
\(360\).
\(120\).
\(15\).
\(20\).
Cho \[\cos \alpha = - \frac{2}{3}\], \[\cos 2\alpha \] nhận giá trị nào trong các giá trị sau?
\( - \frac{2}{3}\).
\( - \frac{4}{3}\).
\( - \frac{1}{9}\).
\(\frac{4}{3}\).
Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất bốn lần. Xác suất để cả bốn lần gieo đều xuất hiện mặt sấp là
\(\frac{4}{{16}}\).
\(\frac{2}{{16}}\).
\(\frac{1}{{16}}\).
\(\frac{6}{{16}}\).
Cho hình chóp\(S.ABCD\) có đáy \(ABCD\) là hình thang \(\left( {AB{\rm{//}}CD} \right)\). Gọi \(M\), \(N\) và \(P\) lần lượt là trung điểm của \(BC\), \(AD\) và \(SA\). Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {MNP} \right)\) là
Đường thẳng \(PM\).
Đường thẳng qua \(S\) và song song với \(AB\).
Đường thẳng qua \(M\) và song song với \(SC\).
Đường thẳng qua \(P\) và song song với \(AB\).
