24 câu hỏi
Gieo một đồng xu cân đối đồng chất liên tiếp 2 lần. Không gian mẫu trong phép thử trên là
B. 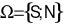 .
.
C.
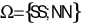 .D.
.D. 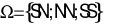 .
.
A. TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Gieo một đồng xu cân đối đồng chất liên tiếp 2 lần. Không gian mẫu trong phép thử trên là
\(\Omega = \left\{ {SN;NS;NN;SS} \right\}\).
\(\Omega = \left\{ {S;N} \right\}\).
\(\Omega = \left\{ {SS;NN} \right\}\).
\(\Omega = \left\{ {SN;NN;SS} \right\}\).
Tập nghiệm của bất phương trình 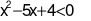 là
là
B.  .
.
D. 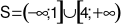 .
.
Tập nghiệm của bất phương trình \({x^2} - 5x + 4 < 0\) là
\(S = \left[ {1;\,4} \right]\).
\(S = \left( {1;\,4} \right)\).
\(S = \left( { - \infty ;\,1} \right) \cup \left( {4;\, + \infty } \right)\).
\(S = \left( { - \infty ;\,1} \right] \cup \left[ {4;\, + \infty } \right)\).
Để đi từ Thọ Xuân (Thanh Hóa) vào Nha Trang (Khánh Hòa) có thể đi bằng một trong các phương tiện: Máy bay hoặc Ôtô. Biết rằng mỗi ngày từ Thọ Xuân vào Nha Trang có:

Trong một ngày, số cách lựa chọn phương tiện để đi từ Thọ Xuân vào Nha Trang là
B. 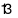 .C.
.C.  .D.
.D. 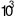 .
.
Để đi từ Thọ Xuân (Thanh Hóa) vào Nha Trang (Khánh Hòa) có thể đi bằng một trong các phương tiện: Máy bay hoặc Ôtô. Biết rằng mỗi ngày từ Thọ Xuân vào Nha Trang có:

Trong một ngày, số cách lựa chọn phương tiện để đi từ Thọ Xuân vào Nha Trang là
\(30\).
\(13\).
\({3^{10}}\).
\({10^3}\).
Góc có số đo 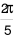 đổi sang độ là:
đổi sang độ là:
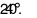 B.
B. 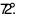 C.
C. 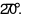 D.
D. 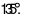
Góc có số đo \(\frac{{2\pi }}{5}\) đổi sang độ là:
\[240^\circ .\]
\[72^\circ .\]
\[270^\circ .\]
\[135^\circ .\]
Trong các hàm số sau, hàm số nào có tập xác định không phải là tập  ?
?
B. 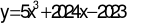 . C.
. C. 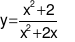 .D.
.D.  .
.
Trong các hàm số sau, hàm số nào có tập xác định không phải là tập \(\mathbb{R}\)?
\[y = \frac{{x + 8}}{{3{x^2} + 1}}\].
\[y = 5{x^3} + 2024x - 2023\].
\[y = \frac{{{x^2} + 2}}{{{x^2} + 2x}}\].
\[y = \frac{{\sqrt {2 + {x^4}} }}{{{x^2} + 4x + 5}}\].
Trong mặt phẳng  , giả sử
, giả sử  lần lượt là vectơ pháp tuyến của đường thẳng
lần lượt là vectơ pháp tuyến của đường thẳng 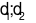 . Gọi
. Gọi 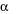 là góc giữa hai đường thẳng
là góc giữa hai đường thẳng 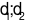 . Chọn mệnh đề đúng.
. Chọn mệnh đề đúng.
B.  .C.
.C. 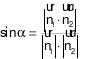 .D.
.D. 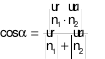 .
.
Trong mặt phẳng \[Oxy\], giả sử \(\overrightarrow {{n_1}} ;\,\overrightarrow {{n_2}} \) lần lượt là vectơ pháp tuyến của đường thẳng \({d_1};\,{d_2}\). Gọi \(\alpha \) là góc giữa hai đường thẳng \({d_1};\,{d_2}\). Chọn mệnh đề đúng.
\[\cos \alpha = \,\,\frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}}\].
\[\cos \alpha = \,\,\frac{{\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}}\].
\[\sin \alpha = \,\,\frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}}\].
\[\cos \alpha = \,\,\frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| + \left| {\overrightarrow {{n_2}} } \right|}}\].
Trong mặt phẳng  , cho đường tròn
, cho đường tròn 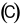 có phương trình
có phương trình 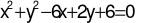 . Tọa độ tâm
. Tọa độ tâm  của đường tròn
của đường tròn 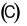 là
là
B. 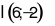 .C.
.C. 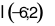 .D.
.D. 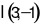 .
.
Trong mặt phẳng \(Oxy\), cho đường tròn \(\left( C \right)\) có phương trình \(\,{x^2} + {y^2} - 6x + 2y + 6 = 0\). Tọa độ tâm \(I\) của đường tròn \(\left( C \right)\) là
\(I\left( { - 3;1} \right)\).
\(I\left( {6; - 2} \right)\).
\(I\left( { - 6;2} \right)\).
\(I\left( {3; - 1} \right)\).
Trong mặt phẳng  , khoảng cách từ điểm
, khoảng cách từ điểm 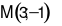 đến đường thẳng
đến đường thẳng  là
là
B. 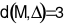 .C.
.C.  .D.
.D.  .
.
Trong mặt phẳng \[Oxy\], khoảng cách từ điểm \(M\left( {3;\, - 1} \right)\) đến đường thẳng \[\Delta :\,\,4x + \,3y + 6 = 0\] là
\[d\left( {M,\Delta } \right) = \,5\].
\[d\left( {M,\Delta } \right) = 3\].
\[d\left( {M,\Delta } \right) = 4\].
\[d\left( {M,\Delta } \right) = \,6\].
Cho hình chóp 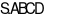 có đáy
có đáy  là hình thang với
là hình thang với  . Trên cạnh
. Trên cạnh 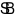 lấy điểm
lấy điểm 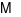 . Gọi
. Gọi  là giao điểm của
là giao điểm của 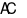 và
và 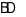 ;
; 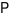 là giao điểm của
là giao điểm của 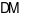 và
và 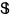 . Giao tuyến của hai mặt phẳng
. Giao tuyến của hai mặt phẳng  và
và 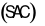 là
là
B.  .C.
.C.  .D.
.D. 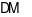 .
.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang với \(AB{\rm{ // }}CD\). Trên cạnh \(SB\) lấy điểm \(M\). Gọi \(I\) là giao điểm của \(AC\) và \(BD\); \(P\) là giao điểm của \(DM\) và \(SI\). Giao tuyến của hai mặt phẳng \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\) là
\(DP\).
\(SI\).
\(AP\).
\(DM\).
Biết  . Tính
. Tính 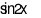 .
.
B.  C.
C.  .D.
.D.  .
.
Biết \(\sin x - \cos x = \frac{{\sqrt 2 }}{3}\). Tính \(\sin 2x\).
\(\frac{7}{9}\).
\( - \frac{7}{9}\)\(.\)
\(\frac{1}{3}\).
\(\frac{{11}}{3}\).
Số cách xếp 6 bạn nam và 5 bạn nữ thành một hàng dọc là
B. 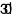 .C.
.C. 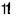 .D.
.D. 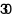 .
.
Số cách xếp 6 bạn nam và 5 bạn nữ thành một hàng dọc là
\(6!\, \cdot 5!\).
\(30!\).
\(11!\).
\(30\).
Cho 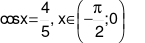 . Giá trị của
. Giá trị của 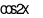 có dạng
có dạng  với
với  là phân số tối giản. Tính
là phân số tối giản. Tính  ta được kết quả là
ta được kết quả là
B. 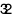 .C.
.C. 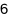 .D.
.D. 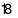 .
.
Cho \[\cos x = \frac{4}{5},{\rm{ }}x \in \left( { - \frac{\pi }{2};0} \right)\]. Giá trị của \[\cos 2x\] có dạng \(\frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản. Tính \(a + b\) ta được kết quả là
\[ - 18\].
\[32\].
\[6\].
\[18\].
