Bộ 3 đề KSCL đầu năm Toán 10 có đáp án - Đề 3
21 câu hỏi
Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Cố lên, sắp đói rồi!
b) Số \[15\] là số nguyên tố.
c) Tổng các góc của một tam giác là \(180^\circ \).
d) \[3\]là số nguyên dương.
\[3\].
\[2\].
\[4\].
\[1\].
Cho góc nhọn \(\alpha \) có \(\tan \alpha = \frac{3}{4}\). Giá trị của \(\cot \alpha \) bằng.
\( - \frac{3}{4}\).
\(\frac{4}{3}\).
\(4\).
\(3\).
Thống kê điểm kiểm tra môn Toán của lớp 10A, ta thu được bảng số liệu sau:
Điểm | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Số học sinh | 2 | 3 | 4 | 8 | 13 | 8 | 7 |
Theo bảng số liệu trên, lớp 10A có bao nhiêu bạn đạt điểm 10?
8.
13.
7.
9.
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3{\rm{\;(cm)}},\,\,AC = 4{\rm{\;(cm)}}{\rm{.}}\) Khẳng định nào sau đây là đúng?
\(\tan B = \frac{4}{3}\).
\(\tan C = \frac{4}{3}\).
\(\cot B = \frac{4}{3}\).
\(\cot C = \frac{3}{4}\).
Hình nón có chiều cao bằng 12 cm, bán kính đáy bằng 9 cm thì diện tích xung quanh là
\(60\;{\rm{c}}{{\rm{m}}^2}\).
\(80\pi \;{\rm{c}}{{\rm{m}}^2}\).
\(135\pi \;{\rm{c}}{{\rm{m}}^2}\).
\(180\pi \;{\rm{c}}{{\rm{m}}^2}\).
Xét mệnh đề chứa biến \(P:\) với \(m\) là tham số. Tìm tất cả các giá trị của tham số \(m\) để mệnh đề \(P\) đúng.
\(m < 1.\)
>
\(m \le 1.\)
\(m > 1.\)
\(m \ge 1.\)
Một hộp đựng \(5\) quả cầu màu xanh, \(3\) quả cầu màu đỏ, \(7\) quả cầu màu trắng có cùng kích thước và khối lượng. Chọn ngẫu nhiên ra một quả cầu. Xác suất của biến cố “Quả cầu được chọn ra màu đỏ” là
\(\frac{1}{5} \cdot \)
\(\frac{2}{{15}} \cdot \)
\(\frac{3}{5} \cdot \)
\(\frac{7}{{15}} \cdot \)
Cho tứ giác \(ABCD\) nội tiếp đường tròn biết \[\widehat A = 3\widehat C\]. Vậy số đo là
\(30^\circ .\)
\[45^\circ .\]
\[90^\circ .\]
\(135^\circ .\)
Mệnh đề . Phủ định của mệnh đề \[P\] là
\(\exists x \in \mathbb{R},{\rm{ }}{x^2} - x + 7 \ge 0\).
\(\forall x \in \mathbb{R},{\rm{ }}{x^2} - x + 7 \ge 0\).
\(\exists x \in \mathbb{R},{\rm{ }}{x^2} - x + 7 > 0\).
\(\forall x \in \mathbb{R},{\rm{ }}{x^2} - x + 7 > 0\).
Nghiệm của bất phương trình \[4x - 2 > 2 + 2x\] là
\[x > 2.\]
\[x < 2.\]
>
\[x \ge 2.\]
\[x \le 2.\]
Điều kiện xác định của phương trình \(\frac{{2x + 1}}{{x - 2}} = \frac{1}{3}\) là
\(x \ne 2\).
\(x \ne - 2\).
\(x \ne 0\).
\(x = 2\).
Cho hai tập \(A = \left\{ {x \in \mathbb{R}|x + 2 \ge 0} \right\}\) và \(B = \left\{ {x \in \mathbb{R}|2x - 1 < 0} \right\}\).
a)\(A = \left[ { - 2; + \infty } \right)\), \(B = \left( { - \infty ;\frac{1}{2}} \right)\).
b) Biểu diễn trên trục số tập hợp \(A\) là
![]()
c)\(A \cap B = \left( { - \infty ; + \infty } \right)\).
d) Số phần tử nguyên của tập hợp \(A \cap B\) là 5.
Phát biểu mệnh đề đảo của mệnh đề: “Nếu n là số tự nhiên thì n là số nguyên”.
“Nếu n là số nguyên thì n là số tự nhiên”.
“Nếu n là số tự nhiên thì n không là số nguyên”.
“Nếu n không là số tự nhiên thì n là số nguyên”
“Nếu n không là số nguyên thì n không là số tự nhiên”.
Cho \({\rm{tan}}\alpha = 3\)và \({\rm{0}}^\circ < \alpha < 90^\circ \).
a)\(\cot \alpha = \frac{1}{3}.\)
b)\(\cos \alpha = \frac{{\sqrt {10} }}{{10}}.\)
c)\(5{\sin ^2}\alpha - 3{\cos ^2}\alpha + \cot \left( {90^\circ - \alpha } \right) = \frac{{36}}{7}\).
d)Giá trị của biểu thức \(E = \frac{{{{\sin }^2}\alpha - 5{{\cos }^2}\alpha }}{{2{{\sin }^2}\alpha + 3\sin \alpha \cos \alpha + {{\cos }^2}\alpha }} = \frac{a}{b}\)với \(\left( {a;b} \right) = 1\) và \(a,b\, \in {\mathbb{N}^*}\). Khi đó \[a + b = 8\].
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
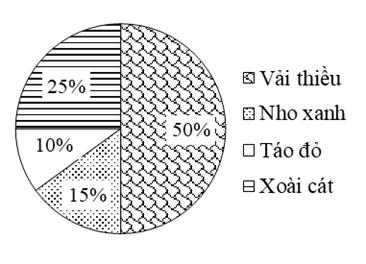
Biểu đồ ở hình dưới cho biết tỉ lệ khối lượng các loại quả bán được trong ngày Chủ nhật của một cửa hàng. Biết khối lượng nho xanh bán được là 24 kg. Khối lượng vải thiều bán được là bao nhiêu?
Quả bóng rổ là một quả bóng hình cầu được sử dụng trong các trận đấu bóng rổ (hình vẽ), kích cỡ quả bóng rổ rất đa dạng dành cho các độ tuổi khác nhau. Quả bóng rổ size 7 có đường kính khoảng 24 cm, đây là kích cỡ bóng chính thức cho bóng rổ nam cấp độ trung học, đại học cũng như chuyên nghiệp. Khi bơm căng thì thể tích của quả bóng rổ size 7 là bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) (kết quả làm tròn đến chữ số hàng đơn vị)?

Từ hai địa điểm \(A,\,\,B\) người ta cùng nhìn thấy một đỉnh núi với góc nâng lần lượt là \(40^\circ \) và \(30^\circ \) (như hình vẽ). Biết khoảng cách giữa hai địa điểm \(A,\,\,B\) là 600 m. Tính chiều cao của ngọn núi (kết quả tính theo đơn vị mét và làm tròn đến chữ số hàng đơn vị).
Bắc có số tiền không vượt quá 60 000 đồng gồm 15 tờ với hai loại mệnh giá 2 000 đồng và 5 000 đồng. Hỏi Bắc có nhiều nhất bao nhiêu tờ tiền mệnh giá 5 000 đồng?
B. TỰ LUẬN
Cho phương trình \({x^2} + 2x + m - 1 = 0\) \((1)\) (với \(m\) là tham số).
1) Giải phương trình \((1)\) khi \(m = - 2\).
2) Tìm giá trị của \(m\) để phương trình \((1)\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 3.\)
Một gia đình có bốn người lớn và ba trẻ em mua vé xem xiếc hết 370 000 đồng. Một gia đình khác có hai người lớn và hai trẻ em cũng mua vé xem xiếc tại rạp đó hết 200 000 đồng. Hỏi giá bán từng loại vé cho người lớn và trẻ em là bao nhiêu? Biết rằng rạp bán hai hạng vé: người lớn và trẻ em, mỗi người vào xem đều phải mua một vé đúng hạng.
Biênđộnhiệtlàkhoảngcáchchênhlệchgiữanhiệtđộcaonhấtvànhiệtđộ thấpnhấttrongcùngmộtkhoảngthờigiannhấtđịnh(mộtngày,mộttháng,mộtnăm,…)của cùng mộtvùngđịalí. Biểuđồcộtképdướiđâybiểudiễnnhiệtđộ(độ C)cácngàytrongmột tuần tại Thành phố Hồ Chí Minh.
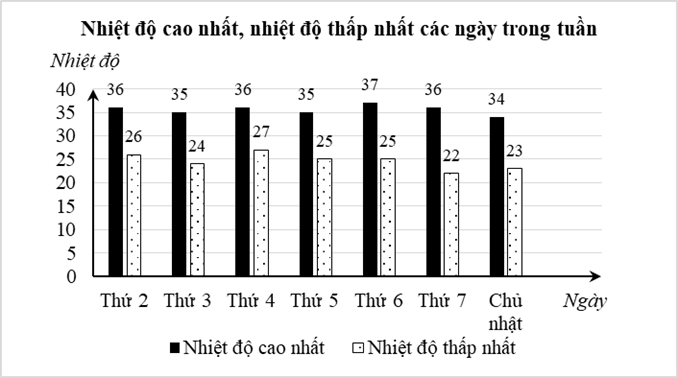
1) Trong tuần này, ngày có biên độ nhiệt lớn nhất của thành phố Hồ Chí Minh là thứ mấy?
2) Chọnngẫunhiênmộtngàytrongtuần,tínhxácsuấtcủa cácbiếncốsau:
A: “Ngày được chọn có nhiệt độ cao nhất không quá35 độC”.
B:“Ngàyđượcchọncóbiênđộnhiệtnhỏhơn12độ C”.


