Bộ 3 đề KSCL đầu năm Toán 10 có đáp án - Đề 2
21 câu hỏi
A. TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Phương trình \(3x - 9 = 0\) có nghiệm là
\(x = 9\).
\(x = - 3\).
\(x = 3\).
\(x = - 9\).
Cho tập hợp \(A = \left\{ {x \in \mathbb{R}| - 3 < x < 1} \right\}\). Tập A là tập nào sau đây?
>
\(\left[ { - 3;1} \right]\).
\(\left\{ { - 3;1} \right\}\).
\(\left[ { - 3;1} \right)\).
\(\left( { - 3;1} \right)\).
Cho đường tròn \[\left( {O\,;\,\,3\,{\rm{cm}}} \right)\] và hai điểm \[A,\,\,B\] thỏa mãn \[OA = 3\,{\rm{cm,}}\,\,OB = 4\,{\rm{cm}}{\rm{.}}\]Khẳng định nào sau đây đúng?
Điểm \[A\] nằm trong \[\left( O \right),\] điểm \[B\] nằm ngoài \[\left( O \right).\]
Điểm \[A\] nằm ngoài \[\left( O \right),\] điểm \[B\] nằm trên \[\left( O \right).\]
Điểm \[A\] nằm trên \[\left( O \right),\] điểm \[B\] nằm ngoài \[\left( O \right).\]
Điểm \[A\] nằm trên \[\left( O \right),\] điểm \[B\] nằm trong \[\left( O \right).\]
Phát biểu nào dưới đây không là một mệnh đề toán học?
\[ax + b = 0\] luôn có nghiệm nguyên.
\(2 < 3\).
>
Hôm nay bạn có học môn Toán không?
\(10 \ge \pi \).
Bất phương trình \(2x + 3 \le 9\) có nghiệm là
\(x < 3\).
>
\(x > 3\).
\(x \le 3\).
\(x \ge 3\).
Đường kính của đường tròn đi qua bốn đỉnh của hình chữ nhật \(MNPQ\) có chiều dài 12 cm, chiều rộng 5 cm là
13 cm.
\(\frac{{13}}{2}\;{\rm{cm}}\).
\(\frac{{13\sqrt 2 }}{2}\;{\rm{cm}}\).
\(\frac{{5\sqrt 2 }}{2}\;{\rm{cm}}\).
Gieo một con xúc xắc 50 lần cho kết quả như sau:
Số chấm xuất hiện | 1 | 2 | 3 | 4 | 5 | 6 |
Tần số | 8 | 7 | ? | 8 | 6 | 11 |
Tần số xuất hiện mặt 3 chấm là
9.
10.
11.
12.
Cho hình vẽ.
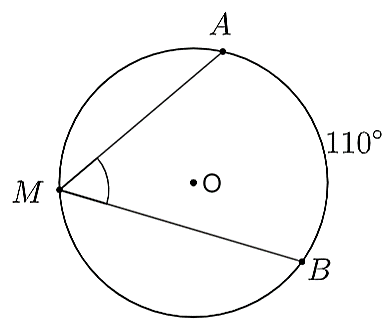
Số đo của góc \[\widehat {AMB}\] là
\[70^\circ .\]
\[220^\circ .\]
\[110^\circ .\]
\[55^\circ .\]
Mệnh đề nào sau là mệnh đề sai?
\(\exists n \in \mathbb{N}:{n^2} = n\).
\(\forall x \in \mathbb{R}:{x^2} > 0\).
\(\exists x \in \mathbb{R}:x > {x^2}\).
\(\forall n \in \mathbb{N}:n \le 2n\).
Cho \(\sin \alpha = \frac{4}{5}\) \(\left( {0^\circ < \alpha < 90^\circ } \right)\). Tính \(\cos \alpha \).
>
\(\cos \alpha = \frac{5}{3}\).
\(\cos \alpha = \frac{3}{5}\).
\(\cos \alpha = - \frac{3}{5}\).
\(\cos \alpha = - \frac{4}{5}\).
Giá trị của \(\sqrt {2024} \) được làm tròn đến chữ số thập phân thứ hai là
\(44,98.\)
\(44,99.\)
\(45.\)
\(44.\)
Cho phương trình bậc hai \(3{x^2} - 5x - 2 = 0\). Biết phương trình có một nghiệm \(x = 2.\) Nghiệm còn lại của phương trình là
\(\frac{{ - 2}}{3}.\)
\(\frac{{ - 1}}{3}.\)
\(\frac{{ - 5}}{3}.\)
\(\frac{{ - 4}}{3}.\)
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Xét hai mệnh đề và .
a) Mệnh đề đảo của mệnh đề \(A \Rightarrow B\) là: Nếu \(a,\,b \in \mathbb{R};\,a > b > 0\) thì \({a^2} > {b^2}\).
b) Mệnh đề \(A \Rightarrow B\) là mệnh đề đúng.
c) Mệnh đề đảo của mệnh đề \(A \Rightarrow B\) là mệnh đề đúng.
d) Mệnh đề \(A \Leftrightarrow B\) là mệnh đề sai.
Một chiếc kem ốc quế có dạng hình nón với phần vỏ quế có đường kính đáylà\[4,4{\rm{ cm,}}\] chiều cao vỏ quế\[12{\rm{ cm}}\,{\rm{.}}\]Người ta lấy phần kem từ một hộp hình trụ có chiều cao là\[15{\rm{ cm}}\]với diện tích đáy \(100\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\) để cho vào vỏ ốc quế(coi phần vỏ kem có độ dày không đáng kể).

a)Thể tích hình trụ có bán kính đáy \(R\) và chiều cao \(h\), được tính bằng công thức: \(V = \frac{1}{3}\pi {R^2}h.\)
b)Bán kính đáy của chiếc kem ốc quế là \(R = 2,2\,\,{\rm{cm}}\,{\rm{.}}\)
c)Thể tích chiếc kem ốc quế là \(\frac{{1452}}{{25}}\pi \,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
d) Nếu lấy kem cho vào phần ốc quế đến sát mép miệng như hình vẽ trên thì ta có thể lấy kem từ hộp làm được tối đa 75 chiếc kem ốc quế, biết rằng trong hộp có đầy kem và phần vỏ hộp có độ dày không đáng kể.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Tính giá trị của biểu thức \(A = \cos 20^\circ + \cos 40^\circ + \cos 60^\circ + ... + \cos 160^\circ + \cos 180^\circ \).
Tháp nghiêng ở thành phố Pisa, Italia nghiêng khoảng \(4^\circ \) so với phương thẳng đứng. Người ta gắn ở mặt ngoài của tháp hai thiết bị tại hai vị trí \(A,\,\,B\) và nối với nhau bởi dây truyền tín hiệu. Tính gần đúng độ dài nhỏ nhất của dây đó, biết \(HB\) gần bằng \(3,146\,\,\;{\rm{m,}}\) với \(H\) là hình chiếu vuông góc của \(A\) trên mặt đất (xem hình vẽ). Kết quả làm tròn đến hàng phần mười theo đơn vị mét.

Quãng đường \(AB\) dài 200 km. Lúc 8 giờ, một xe tải đi từ \[A\] đến \(B;\) 40 phút sau, một xe con cũng đi từ \[A\] đến \[B\] với vận tốc lớn hơn vận tốc xe tải 10 km/h. Hai xe đến \[B\] cùng một lúc. Hỏi hai xe đến \[B\] lúc mấy giờ?
Quan hệ giữa quãng đường chuyển động \(y\,\,({\rm{m}})\) và thời gian chuyển động \(x\) (giây) của một vật rơi tự do được biểu diễn gần đúng bởi công thức \(y = 5{x^2}\). Nếu thả một vật nặng từ độ cao 120 m xuống đất (coi sức cản của không khí không đáng kể) thì sau khi thả được bao nhiêu giây vật đó sẽ cách mặt đất một khoảng 40 m?
B. TỰ LUẬN
Cho hai tập hợp \[A = \left[ { - 2;4} \right]\] và \(B = \left( {1;5} \right)\). Xác định tập hợp \(A \cup B,A \cap B\) và biểu diễn chúng trên trục số?
Có 6 quả bóng có cùng kích thước và khối lượng, mỗi quả bóng ghi một trong các số từ 10 đến 15 được để vào hai chiếc hộp. Hộp màu xanh chứa các quả bóng ghi số chẵn, hộp màu vàng chứa các quả bóng ghi số lẻ. Hai bạn Hà và Mạnh chơi một trò chơi như sau: Hà lấy ngẫu nhiên một quả bóng ở hộp màu xanh, Mạnh lấy ngẫu nhiên một quả bóng ở hộp màu vàng và xem số được ghi trên hai quả bóng, bạn nào lấy được quả bóng có số lớn hơn thì thắng.
a) Mô tả không gian mẫu của phép thử trên.
b) Tính xác suất của biến cố B: “Hà chọn được quả bóng có số lớn hơn của Mạnh”.
Tại cùng một thời điểm, có hai người đang ở hai vị trí \[A\] và \[B\] cách nhau \[1000\] mét. Người thứ nhất ở vị trí \[B\] và đi về phía điểm \[A\] với vận tốc \[2{\rm{\;m/s}}\] và người thứ hai ở vị trí \[A\] đi về phía điểm \[C\] với vận tốc \[1,5{\rm{\;m/s}}.\] Biết rằng \[AB\] và \[AC\] vuông góc với nhau. Hãy cho biết sau bao nhiêu giây thì khoảng cách giữa hai người này nhỏ nhất?


