Bộ 25 đề thi học kì 1 Toán 12 năm 2022-2023 (tiếp theo) - Đề 32 có đáp án
50 câu hỏi
Cho hàm số \(y = {x^4} - 2m{x^2} + m\left( C \right)\) với m là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm tham số m để tiếp tuyến \(\Delta \) với đồ thị (C) tại A cắt đường tròn \(\left( T \right):{x^2} + {\left( {y - 1} \right)^2} = 4\) tạo thành một dây cung có độ dài nhỏ nhất.
\(m = \frac{{16}}{{13}}\)
\(m = - \frac{{13}}{{16}}\)
\(m = \frac{{13}}{{16}}\)
\(m = - \frac{{16}}{{13}}\)
Có bao nhiêu loại khối đa điện đều mà mỗi mặt của nó là một tam giác đều?
3
1
5
2
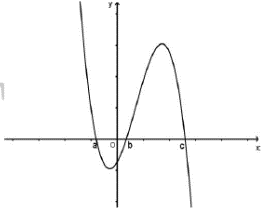
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) cắt trục Ox tại ba điểm có hoành độ \(a < b < c\) như hình vẽ. Xét 4 mệnh đề sau:
\(\left( 1 \right):f\left( c \right) > f\left( a \right) > f\left( b \right)\)
\(\left( 2 \right):f\left( c \right) > f\left( b \right) > f\left( a \right)\)
\(\left( 3 \right):f\left( a \right) > f\left( b \right) > f\left( c \right)\)
\(\left( 4 \right):f\left( a \right) > f\left( b \right)\)
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
4
1
2
3
Cho một đa giác đều 2n đỉnh \(\left( {n \ge 2,\,\,n \in N} \right)\). Tìm n biết số hình chữ nhật được tạo ra từ bốn đỉnh trong số 2n đỉnh của đa giác đó là 45.
\(n = 12\)
\(n = 10\)
\(n = 9\)
\(n = 45\)
Cho \(\int\limits_{ - 1}^5 {f\left( x \right)dx} = 4\). Tính \(I = \int\limits_{ - 1}^2 {f\left( {2x + 1} \right)dx} \)
\(I = 2\)
\(I = \frac{5}{2}\)
\(I = 4\)
\(I = \frac{3}{2}\)
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( P \right):x + \left( {m + 1} \right)y - 2z + m = 0\) và \(\left( Q \right):2x - y + 3 = 0\), với m là tham số thực. Để \(\left( P \right)\) và \(\left( Q \right)\) vuông góc thì giá trị của bằng bao nhiêu?
\(m = - 5\)
\(m = 1\)
\(m = 3\)
\(m = - 1\)
Cho bốn mệnh đề sau:
\(\left( I \right):\int {{{\cos }^2}x\,dx = \frac{{{{\cos }^3}x}}{3} + C} \) \(\left( {II} \right):\int {\frac{{2x + 1}}{{{x^2} + x + 2018}}dx = \ln \left( {{x^2} + x + 2018} \right) + C} \)
\(\left( {III} \right):\int {{3^x}\left( {{2^x} + {3^{ - x}}} \right)dx = \frac{{{6^x}}}{{\ln 6}} + x + C} \) \(\left( {IV} \right):\int {{3^x}dx = {3^x}} .\ln 3 + C\)
Trong các mệnh đề trên có bao nhiêu mệnh đề sai?
3
1
2
4
Cho hình chóp S.ABC có SA vuông góc mặt phẳng \(\left( {ABC} \right)\), tam giác ABC vuông tại B. Biết \(SA = 2a,\,\,AB = a,\,\,BC = a\sqrt 3 \). Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
a
2a
\(a\sqrt 2 \)
\(2a\sqrt 2 \)
Cho hàm số \(y = \frac{{2x - 1}}{{x - 1}}\) có đồ thị \(\left( C \right)\). Tìm tất cả các giá trị thực của tham số m để đường thẳng \(d:y = x + m\) và cắt (C) tại hai điểm phân biệt A, B sao cho \(AB = 4\)
\(m = - 1\)
\(\left[ \begin{array}{l}m = 0\\m = 3\end{array} \right.\)
\(\left[ \begin{array}{l}m = - 1\\m = 3\end{array} \right.\)
\(m = 4\)
Tìm tập xác định D của hàm số \(y = \frac{{\tan x - 1}}{{\sin x}} + \cos \left( {x + \frac{\pi }{3}} \right)\) .
\(D = R\backslash \left\{ {k\pi ,\,\,k \in Z} \right\}\)
\(D = R\backslash \left\{ {\frac{{k\pi }}{2},\,\,k \in Z} \right\}\)
\(D = R\backslash \left\{ {\frac{\pi }{2} + k\pi ,\,\,k \in Z} \right\}\)
\(D = R\)
Khẳng định nào sau đây là khẳng định sai?
\(\cos \,x = - 1 \Leftrightarrow x = \pi + k2\pi \)
\(\cos \,x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi \)
\(\cos \,x = 1 \Leftrightarrow x = k2\pi \)
\(\cos \,x = 0 \Leftrightarrow x = \frac{\pi }{2} + k2\pi \)
Tập nghiệm của phương trình \({9^x} - {4.3^x} + 3 = 0\) là:
\(\left\{ {0;1} \right\}\)
\(\left\{ {1;3} \right\}\)
\(\left\{ {0; - 1} \right\}\)
\(\left\{ {1; - 3} \right\}\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành thỏa mãn \(AB = a,\,\,AC = a\sqrt 3 ,\,\,BC = 2a\). Biết tam giác SBC cân tại S, tam giác SCD vuông tại C và khoảng cách từ D đến mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 3 }}{3}\). Tính thể tích V của khối chóp đã cho.
\(V = \frac{{2{a^3}}}{{3\sqrt 5 }}\)
\(V = \frac{{{a^3}}}{{3\sqrt 5 }}\)
\(V = \frac{{{a^3}}}{{3\sqrt 3 }}\)
\(V = \frac{{{a^3}}}{{\sqrt 5 }}\)
Trong không gian với hệ tọa độ Oxyz , mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 4x + 2y - 6z + 4 = 0\) có bán kính R là
\(R = \sqrt {53} \)
\(R = 4\sqrt 2 \)
\(R = \sqrt {10} \)
\(R = 3\sqrt 7 \)
Một người dùng một cái ca hình bán cầu (Một nửa hình cầu) có bán kính là 3cm để múc nước đổ vào một cái thùng hình trụ chiều cao 10cm và bán kính đáy bằng 6cm. Hỏi người ấy sau bao nhiêu lần đổ thì nước đầy thùng? (Biết mỗi lần đổ, nước trong ca luôn đầy.)
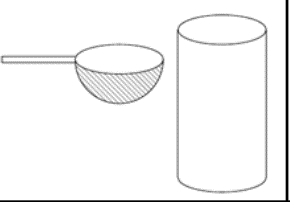
10 lần
24 lần
12 lần
20 lần
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên R và có đồ thị của hàm \(y = f'\left( x \right)\) như hình vẽ. Xét hàm số \(g\left( x \right) = f\left( {2 - {x^2}} \right)\). Mệnh đề nào dưới đây đúng ?
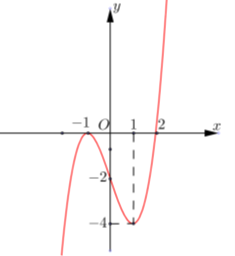
Hàm số \(f\left( x \right)\) đạt cực trị tại \(x = 2\)
Hàm số \(f\left( x \right)\) nghịch biến trên \(\left( { - \infty ;2} \right)\)
Hàm số \(g\left( x \right)\) đồng biến trên \(\left( {2; + \infty } \right)\)
Hàm số \(g\left( x \right)\) nghịch biến trên \(\left( { - 1;0} \right)\)
Tìm tham số m để hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {m + 2} \right)x + 2018\) không có cực trị.
\(m \le - 1\) hoặc \(m \ge 2\)
\(m \le - 1\)
\(m \ge 2\)
\( - 1 \le m \le 2\)
Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?
\(y = - x\sqrt 2 + 1\)
\(y = {x^3} - 3x + 1\)
\(y = {x^2} + 1\)
\(y = {x^3} + 3x + 1\)
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Tính diện tích toàn phần của hình trụ đã cho.
\(9{a^2}\pi \)
\(\frac{{9\pi {a^2}}}{2}\)
\(\frac{{13\pi {a^2}}}{6}\)
\(\frac{{27\pi {a^2}}}{2}\)
Tìm tập xác định của hàm số \(f\left( x \right) = {\left( {1 + \sqrt {x - 1} } \right)^{\sqrt 5 }}\)
\(D = \mathbb{R}\)
\(D = \left[ {1; + \infty } \right)\)
\(D = \left( {0; + \infty } \right)\)
\(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
Cho hai số phức \({x_1} = 2 + 3i\) và \({z_2} = - 3 - 5i\). Tính tổng phần thực và phần ảo của số phức \[{\rm{w}} = {z_1} + {z_2}\]
3
0
\( - 1 - 2i\)
–3
Cho hàm số \(y = x{\mathop{\rm lnx}\nolimits} \). Chọn khẳng định sai trong số các khẳng định sau:
. Hàm số đồng biến trên khoảng \(\left( {\frac{1}{e}; + \infty } \right)\)
Hàm số đồng biến trên khoảng \(\left( {\frac{1}{e}; + \infty } \right)\)
Hàm số có đạo hàm \(y' = 1 + \ln x\)
Hàm số có tập xác định là \(D = \left( {0; + \infty } \right)\)
Có bao nhiêu số tự nhiên có ba chữ số dạng \(\overline {abc} \) với \(a,b,c \in \left\{ {0;1;2;3;4;5;6} \right\}\) sao cho \(a < b < c\).
120
30
40
20
Cho lăng trụ đứng ABC.A’B’C’ có \(AA' = a\), đáy ABC là tam giác vuông cân tại A và \(AB = a\). Tính thể tích V của khối lăng trụ đã cho.
\(V = \frac{{{a^3}}}{2}\)
\(V = {a^3}\)
\(V = \frac{{{a^3}}}{3}\)
\(V = \frac{{{a^3}}}{6}\)
Tính đạo hàm của hàm số \(y = {\log _2}\left( {x + {e^x}} \right)\)
\(\frac{{1 + {e^x}}}{{\ln 2}}\)
\(\frac{{1 + {e^x}}}{{\left( {x + {e^x}} \right)\ln 2}}\)
\(\frac{{1 + {e^x}}}{{x + {e^x}}}\)
\(\frac{1}{{\left( {x + {e^x}} \right)\ln 2}}\)
Cho tam giác ABC vuông tại A, \(AB = 6cm,\,\,AC = 8cm\). Gọi \({V_1}\) là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AB và \({V_2}\) là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AC. Khi đó, tỷ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng:
\(\frac{{16}}{9}\)
\(\frac{4}{3}\)
\(\frac{3}{4}\)
\(\frac{9}{{16}}\)
Cho hàm số \(f\left( x \right)\) có đạo hàm là \(f'\left( x \right) = \left( {{x^2} - 1} \right){\left( {x - \sqrt 3 } \right)^2}\). Số điểm cực trị của hàm số này là
1
2
3
4
Xét các số thực a, b thỏa mãn điều kiện \(\frac{1}{3} < b < a < 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = {\log _a}\left( {\frac{{3b - 1}}{4}} \right) + 12\log _{\frac{b}{a}}^2a - 3\)
\(Min\,P = 13\)
\(Min\,P = \frac{1}{{\sqrt[3]{2}}}\)
\(Min\,P = 9\)
\(Min\,P = \sqrt[3]{2}\)
Cho hình phẳng D giới hạn bởi đường cong \(y = \sqrt {2 + \cos \,x} \), trục hoành và các đường thẳng \(x = 0,\,\,x = \frac{\pi }{2}\). Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?
\(V = \pi - 1\)
\(V = \pi + 1\)
\(V = \pi \left( {\pi - 1} \right)\)
\(V = \pi \left( {\pi + 1} \right)\)
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt.
Năm mặt.
Ba mặt.
Bốn mặt.
Hai mặt.
Giải phương trình \(\cos 2x + 5sin\,x - 4 = 0\)
\(x = \frac{\pi }{2} + k\pi \)
\(x = - \frac{\pi }{2} + k\pi \)
\(x = k2\pi \)
\(x = \frac{\pi }{2} + k2\pi \)
Tìm giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} - 3{x^2} - 9x + 10\) trên \(\left[ { - 2;2} \right]\)
\(\mathop {max}\limits_{\left[ { - 2;2} \right]} f\left( x \right) = 17\)
\(\mathop {max}\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 15\)
\(\mathop {max}\limits_{\left[ { - 2;2} \right]} f\left( x \right) = 15\)
\(\mathop {max}\limits_{\left[ { - 2;2} \right]} f\left( x \right) = 5\)
Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động, trong đó 2 học sinh nam?
\(C_6^2 + C_9^4\)
\(C_6^2.C_9^4\)
\(A_6^2.A_9^4\)
\(C_9^2.C_6^4\)
Cho số phức z thỏa mãn \(z + 4\overline z = 7 + i\left( {z - 7} \right)\). Khi đó, môđun của z bằng bao nhiêu?
\(\left| z \right| = 5\)
\(\left| z \right| = \sqrt 3 \)
\(\left| z \right| = \sqrt 5 \)
\(\left| z \right| = 3\)
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều. Mặt phẳng \(\left( {A'BC} \right)\) tạo với đáy góc \({30^0}\) và tam giác A’BC có diện tích bằng \(8{a^2}\). Tính thể tích V của khối lăng trụ đã cho.
\(V = 8\sqrt 3 {a^3}\)
\(V = 2\sqrt 3 {a^3}\)
\(V = 64\sqrt 3 {a^3}\)
\(V = 16\sqrt 3 {a^3}\)
Cho các chữ số 0, 1, 2, 3, 4, 5 . Từ các chữ số đã cho lập được bao nhiêu số tự nhiên chẵn có 4 chữ số và các chữ số đôi một bất kỳ khác nhau.
160
156
752
240
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(M\left( {0; - 1;2} \right)\) và \(M\left( { - 1;1;3} \right)\). Một mặt phẳng \(\left( P \right)\) đi qua M, N sao cho khoảng cách từ điểm \(K\left( {0;0;2} \right)\) đến mặt phẳng \(\left( P \right)\) đạt giá trị lớn nhất. Tìm tọa độ véctơ pháp tuyến \(\overrightarrow n \) của mặt phẳng \(\left( P \right)\).
\(\overrightarrow n \left( {1; - 1;1} \right)\)
\(\overrightarrow n \left( {1;1; - 1} \right)\)
\(\overrightarrow n \left( {2; - 1;1} \right)\)
\(\overrightarrow n \left( {2;1; - 1} \right)\)
Cho số phức z thỏa mãn \(\left( {1 + 3i} \right)z - 5 = 7i\). Mệnh đề nào sau đây là mệnh đề đúng?
\(\overline z = - \frac{{13}}{5} + \frac{4}{5}i\)
\(\overline z = \frac{{13}}{5} - \frac{4}{5}i\)
\(\overline z = - \frac{{13}}{5} - \frac{4}{5}i\)
\(\overline z = \frac{{13}}{5} + \frac{4}{5}i\)
Cho số phức z và w thỏa mãn \(z + {\rm{w}} = 3 + 4i\) và \(\left| {z - {\rm{w}}} \right| = 9\). Tìm giá trị lớn nhất của biểu thức \(T = \left| z \right| + \left| {\rm{w}} \right|\)
\(Max\,T = \sqrt {176} \)
\(Max\,T = 14\)
\(Max\,T = 4\)
\(Max\,T = \sqrt {106} \)
Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức \({z_1} = - 1 + i\), \({z_2} = 1 + 2i,\,\,{z_2} = 2 - i,\,\,{z_4} = - 3i\). Gọi S diện tích tứ giác ABCD. Tính S.
\(S = \frac{{17}}{2}\)
\(S = \frac{{19}}{2}\)
\(S = \frac{{23}}{2}\)
\(S = \frac{{21}}{2}\)
Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bởi hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía ngoài ta được hình 2. Khi quay hình 2 xung quanh trục d ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
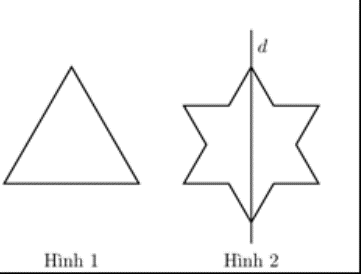
\(\frac{{5\pi \sqrt 3 }}{3}\)
\(\frac{{9\pi \sqrt 3 }}{3}\)
\(\frac{{7\pi \sqrt 3 }}{3}\)
\(\frac{{5\pi \sqrt 3 }}{2}\)
Trong không gian với hệ tọa độ Oxyz , cho hai điểm \(M\left( {2; - 3;5} \right),\,\,N\left( {6; - 4; - 1} \right)\) và đặt \(L = \left| {\overrightarrow {MN} } \right|\). Mệnh đề nào sau đây là mệnh đề đúng?
\(L = \left( {4; - 1; - 6} \right)\)
\(L = \sqrt {53} \)
\(L = 3\sqrt {11} \)
\(L = \left( { - 4;1;6} \right)\)
Tìm tham số m để phương trình \({\log _{\sqrt {2018} }}\left( {x - 2} \right) = {\log _{2018}}\left( {mx} \right)\) có nghiệm thực duy nhất.
\(1 < m < 2\)
\(m > 1\)
\(m > 0\)
\(m < 2\)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \(\left( P \right):x - 2y + 2z - 2 = 0\) và điểm \(I\left( { - 1;2; - 1} \right)\). Viết phương trình mặt cầu \(\left( S \right)\) có tâm và cắt mặt phẳng \(\left( P \right)\) theo giao tuyến là đường tròn có bán kính bằng 5.
\(\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 25\)
\(\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 16\)
\(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 1} \right)^2} = 34\)
\(\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 34\)
Trong không gian với hệ tọa độ Oxyz, mặt phẳng chứa hai điểm \(A\left( {1;0;1} \right),\,\,B\left( { - 1;2;2} \right)\) và song song với trục Ox có phương trình là:
\(y - 2z + 2 = 0\)
\(x + 2z - 3 = 0\)
\(2y - z + 1 = 0\)
\(x + y - z = 0\)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d vuông góc với mặt phẳng \(\left( P \right):4x - z + 3 = 0\). Véc-tơ nào dưới đây là một véctơ chỉ phương của đường thẳng d ?
\(\overrightarrow {{u_1}} \left( {4;1; - 1} \right)\)
\(\overrightarrow {{u_2}} \left( {4; - 1;3} \right)\)
\(\overrightarrow {{u_3}} \left( {4;0; - 1} \right)\)
\(\overrightarrow {{u_4}} \left( {4;1;3} \right)\)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm \(A\left( {a;0;0} \right),\,\,B\left( {0;b;0} \right),\,\,C\left( {0;0;c} \right)\) với a,b,c là các số thực dương thay đổi tùy ý sao cho \({a^2} + {b^2} + {c^2} = 3\). Khoảng cách từ đến mặt O phẳng \(\left( {ABC} \right)\)lớn nhất bằng:
\(\frac{1}{3}\)
3
\(\frac{1}{{\sqrt 3 }}\)
1
Đường tiệm cận ngang của đồ thị hàm số \(y = 1 + \frac{{2x + 1}}{{x + 2}}\) có phương trình là:
\(x = - 2\)
\(y = 3\)
\(x = - 1\)
\(y = 2\)
Tìm nguyên hàm của hàm số \(f\left( x \right) = \sin 3x\)
\(\int {\sin 3x\,dx = - \frac{{\cos 3x}}{3} + C} \)
\(\int {\sin 3x\,dx = \frac{{\cos 3x}}{3} + C} \)
\(\int {\sin 3x\,dx = - \frac{{\sin 3x}}{3} + C} \)
\(\int {\sin 3x\,dx = - \cos 3x + C} \)
Giải phương trình \(\cos 5x.\cos \,x = \cos 4x\)
\(x = \frac{{k\pi }}{5}\left( {k \in Z} \right)\)
\(x = \frac{{k\pi }}{3}\left( {k \in Z} \right)\)
\(x = k\pi \left( {k \in Z} \right)\)
\(x = \frac{{k\pi }}{7}\left( {k \in Z} \right)\)