Bộ 25 đề thi học kì 1 Toán 12 năm 2022-2023 (tiếp theo) - Đề 27 có đáp án
50 câu hỏi
Cho hình nón đỉnh S có đường cao bằng 6cm, bán kính đáy bằng 10cm. Trên đường tròn đáy lấy hai điểm A, B sao cho \(AB = 12cm\). Diện tích tam giác bằng:
\(100\,c{m^2}\)
\(48\,c{m^2}\)
\(40\,c{m^2}\)
\(60\,c{m^2}\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm sao cho \(SE = 2EC\). Tính thể tích của khối tứ diện SEBD.
\(V = \frac{1}{3}\)
\(V = \frac{2}{3}\)
\(\frac{1}{6}\)
\(V = \frac{1}{{12}}\)
Cho \({\log _2}3 = a\). Hãy tính \({\log _4}54\) theo a.
\({\log _4}54 = \frac{1}{2}\left( {1 + 3a} \right)\)
\({\log _4}54 = \frac{1}{2}\left( {1 + 6a} \right)\)
\({\log _4}54 = \frac{1}{2}\left( {1 + 3a} \right)\)
\({\log _4}54 = 2\left( {1 + 6a} \right)\)
- Giải bất phương trình \({\left( {\sqrt {10} - 3} \right)^x} > \sqrt {10} + 3\) có kết quả là:
\(x < 1\)
\(x > 1\)
\(x < - 1\)
\(x > - 1\)
Đồ thị bên là của hàm số nào:
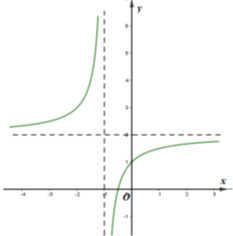
\(y = \frac{{2x - 1}}{{x - 1}}\)
\(y = \frac{{2x + 5}}{{x + 1}}\)
\(y = \frac{{x + 2}}{{x + 1}}\)
\(y = \frac{{2x + 1}}{{x + 1}}\
Phương trình \({3^{2x + 1}} - {4.3^x} \({x_1},\,{x_2}\) trong đó \({x_1} < {x_2}\), chọn phát biểu đúng.
\({x_1}.{x_2} = - 1\)
\(2{x_1} + {x_2} = 0\)
\({x_1} + 2{x_2} = - 1\)
\({x_1} + {x_2} = - 2\)
Tính đạo hàm của hàm số \(y = x\ln x\)
\(y' = \ln x + 1\)
\(y' = \ln x\)
\(y' = \ln x - 1\)
\(y' = \frac{1}{x}\)
Các điểm cực đại của hàm số \(y = x - \sin 2x\) là:
\(x = \pm \frac{\pi }{6} + k\pi ,\,\,k \in Z\)
\(x = - \frac{\pi }{6} + k\pi ,\,\,k \in Z\)
\(x = \frac{\pi }{6} + k\pi ,\,\,k \in Z\)
\(x = \pm \frac{\pi }{3} + k2\pi ,\,\,k \in Z\)z
Cho khối chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\); tam giác ABC vuông tại A, biết \(BC = 3a;\,\,\,AB = a\). Góc giữa mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \({45^0}\). Tính thể tích khối chóp S.ABC theo a.
\({V_{S.ABC}} = \frac{{4{a^3}}}{9}\)
\({V_{S.ABC}} = \frac{{{a^3}\sqrt 2 }}{6}\)
\({V_{S.ABC}} = \frac{{{a^3}\sqrt 2 }}{2}\)
\({V_{S.ABC}} = \frac{{2{a^3}}}{9}\)
Khối nón có chiều cao \(h = 3cm\) và bán kính đáy \(r = 2cm\) thì có thể tích bằng:
\(16\pi \,c{m^2}\)
\(4\pi \,c{m^2}\)
\(\frac{4}{3}\pi \,c{m^2}\)
\(4\pi \,c{m^2}\)
Giá trị nhỏ nhất của số thực m để hàm số \(y = \frac{1}{3}{x^3} + m{x^2} - mx - m\) đồng biến trên \(\mathbb{R}\) là:
\(m = - 2\)
\(m = 1\)
\(m = - 1\)
\(m = 0\)
Giải phương trình \({\log _6}{x^2} = 2\) được kết quả là:
\(x \in \left\{ { \pm 36} \right\}\)
\(x \in \left\{ { \pm 6} \right\}\)
\(x \in \left\{ { \pm \sqrt 6 } \right\}\)
\(x = 6\)
Cho lăng trụ tứ giác đều ABCD.A’B’C’D’ có đáy là hình vuông cạnh a, \(AA' = 3a\). Thể tích khối lăng trụ đã cho là:
\(12{a^3}\)
\({a^3}\)
\(6{a^3}\)
\(3{a^3}\)
Khối chóp ngũ giác có số cạnh là:
20
15
5
10
Tìm các giá trị thực của tham số m sao cho phương trình \({x^3} - 3x + 4m - 1 = 0\) có ít nhất một nghiệm thực trong đoạn \(\left[ { - 3;4} \right]\)?
\(\frac{{ - 51}}{4} \le m \le \frac{{19}}{4}\)
\(\frac{{ - 51}}{4} < m < \frac{{19}}{4}\)
\( - 51 < m < 19\)
\( - 51 \le m \le 19\)
Giá trị lớn nhất của hàm số \(f\left( x \right) = \frac{{mx - 1}}{{2x + m}}\) trên đoạn \(\left[ {3;5} \right]\) bằng 2 khi và chỉ khi:
\(m = 7\)
\(m = \left\{ {7;13} \right\}\)
\(m \in \emptyset \)
\(m = 13\)
Cho hình chóp S.ABC có \(SA = a,\,\,SB = b,\,\,SC = c\) và \(ASB = BSC = CSA = {60^0}\). Tính thể tích của khối chóp S.ABC.
\(\frac{{\sqrt 2 }}{{12abc}}\)
\(\frac{{\sqrt 2 }}{{12}}abc\)
\(\frac{{\sqrt 2 }}{4}abc\)
\(\frac{{\sqrt 2 }}{{4abc}}\)
Giá trị nhỏ nhất của hàm số \(y = x\sqrt {1 - {x^2}} \) là:
2
1
–1
\(\frac{{ - 1}}{2}\)
Gọi M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 2{\sin ^2}x - \cos \,x + 1\). Thể thì M.m bằng:
\(\frac{{25}}{4}\)
\(\frac{{25}}{8}\)
2
0
Khối đa diện đều loại \(\left\{ {4;3} \right\}\) có số đỉnh, số cạnh và số mặt lần lượt bằng:
6, 12, 8.
8, 12, 6.
12, 30, 20.
4, 6, 4.
Cho bất phương trình \({\log _{\frac{1}{5}}}f\left( x \right) > {\log _{\frac{1}{5}}}g\left( x \right)\). Khi đó, bất phương trình tương đương:
\(f\left( x \right) < g\left( x \right)\)
\(g\left( x \right) > f\left( x \right) \ge 0\)
\(g\left( x \right) > f\left( x \right) > 0\)
\(f\left( x \right) > g\left( x \right)\)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right)\) và\(SA = a\sqrt 3 \). Thể tích của khối chóp S.ABCD là:
\(\frac{{{a^3}\sqrt 3 }}{3}\)
\(\frac{{{a^3}\sqrt 3 }}{6}\)
\(\frac{{{a^3}\sqrt 2 }}{3}\)
\(\frac{{{a^3}\sqrt 2 }}{6}\)
Cho các số thực x, y và a thỏa mãn \(x > y;\,\,a > 1\). Khi đó
\({a^x} < {a^y}\)
\({a^x} \le {a^y}\)
\({a^x} > {a^y}\)
\({a^x} \ge {a^y}\)
Ông An gửi số tiền 100 triệu đồng vào ngân hàng với lãi suất 7%/năm, biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Sau thời gian 10 năm nếu không rút lần nào thì số tiền mà ông An nhận được tính cả gốc lẫn lãi là (đơn vị đồng):
\({10^8}{\left( {1 + 0,0007} \right)^{10}}\)
\({10^8}{\left( {1 + 0,07} \right)^{10}}\)
\({10^8}.0,{07^{10}}\)
\({10^8}{\left( {1 + 0,7} \right)^{10}}\)
Cho hàm số \(y = {x^3} - 3{x^2} + 2\), hãy chọn khẳng định đúng:
Hàm số có đúng ba điểm cực trị.
Hàm số có đúng hai điểm cực trị.
Hàm số có đúng hai điểm cực trị.
Hàm số không có điểm cực trị.
Giải bất phương trình \({\log _{\frac{1}{5}}}\left( {5x - 3} \right) > - 2\), có nghiệm là:
\(x > \frac{{28}}{5}\)
\(\frac{3}{5} < x < \frac{{28}}{5}\)
\(\frac{3}{5} \le x < \frac{{28}}{5}\)
\(x < \frac{{28}}{5}\)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc tạo bởi mặt bên và mặt đáy là \(\alpha \). Thể tích khối chóp S.ABCD là:
\(\frac{{{a^3}\tan \alpha }}{2}\)
\(\frac{{{a^3}\tan \alpha }}{3}\)
\(\frac{{{a^3}\tan \alpha }}{6}\)
\(\frac{{2{a^3}\tan \alpha }}{3}\)
Giả sử A và B là các giao điểm của đường cong \(y = {x^3} - 3x + 2\) và trục hoành. Tính độ dài đoạn thẳng AB:
\(AB = 6\sqrt 5 \)
\(AB = 4\sqrt 2 \)
\(AB = 3\)
\(AB = 5\sqrt 3 \)
Cho hàm số \(y = {x^3} - 2m{x^2} + 1\) có đồ thị \(\left( {{C_m}} \right)\). Tìm m sao cho \(\left( {{C_m}} \right)\) cắt đường thẳng \(d:y = x + 1\) tại ba điểm phân biệt có hoành độ \({x_1},\,{x_2},\,{x_3}\) thỏa mãn \({x_1} + {x_2} + {x_3} = 101\)
\(m = \frac{{101}}{2}\)
\(m = 50\)
\(m = 51\)
\(m = 49\)
Số tiệm cận của đồ thị hàm số \(y = \frac{{{x^2} - 6x + 3}}{{{x^2} - 3x + 2}}\) là
6
2
1
3
Đồ thị bên là của hàm số nào?
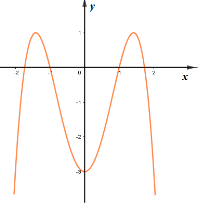
\(y = - {x^4} + 4{x^2} - 3\)
\(y = {x^4} - 3{x^2} - 3\)
\(y = {x^4} + 2{x^2} - 3\)
\(y = - \frac{1}{4}{x^4} + 3{x^2} - 3\)
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị trong hình bên. Hỏi phương trình \(y = a{x^3} + b{x^2} + cx + 2 = 0\) có bao nhiêu nghiệm?
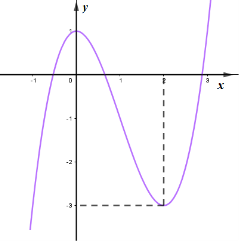
Phương trình có đúng một nghiệm.
Phương trình có đúng hai nghiệm.
Phương trình không có nghiệm.
Phương trình có đúng ba nghiệm
Phương trình \({\log ^2}x - \log x - 2 = 0\) có bao nhiêu nghiệm?
1
2
3
0
Cho lăng trụ tam giác đều tất cả các cạnh bằng a. Một hình trụ tròn xoay có hai đáy là hai hình tròn ngoại tiếp hai đáy của lăng trụ. Thể tích của khối trụ tròn xoay bằng:
\(\frac{{\pi {a^3}}}{9}\)
\(\pi {a^3}\)
\(3\pi {a^3}\)
\(\frac{{\pi {a^3}}}{3}\)
Cho hình trụ (T) có độ dài đường sinh l, bán kính đáy r. Kí hiệu \({S_{xq}}\) là diện tích xung quanh của (T). Công thức nào sau đây đúng?
\({S_{xq}} = 3\pi rl\)
\({S_{xq}} = 2\pi rl\)
\({S_{xq}} = \pi rl\)
\({S_{xq}} = 2\pi {r^2}l\)
Điều kiện cần và đủ của tham số m để hàm số \(y = {x^3} - {x^2} + mx - 5\) có cực trị là:
\(m > \frac{1}{3}\)
\(m < \frac{1}{3}\)
\(m \le \frac{1}{3}\)
\(m \ge \frac{1}{3}\)
Tập xác định của hàm số \(y = {\log _2}\frac{{x + 3}}{{2 - x}}\) là:
\(\left[ { - 3;2} \right]\)
\(\left( { - \infty ; - 3} \right) \cup \left( {2; + \infty } \right)\)
\(R\backslash \left\{ 2 \right\}\)
\(\left( { - 3;2} \right)\)
Cho hình chóp S.ABC có tam giác ABC đều cạnh \(a = 3cm,\,\,SA \bot \left( {ABC} \right)\) và \(SA = 2a\). Tính thể tích khối cầu ngoại tiếp hình chóp \(S.ABC\)
\(\frac{{8{a^3}\pi }}{{3\sqrt 3 }}c{m^3}\)
\(\frac{{4{a^3}\pi }}{3}c{m^3}\)
\(32\pi \sqrt 3 \,c{m^3}\)
\(16\pi \sqrt 3 \,c{m^3}\)
Cho hình lăng trụ đứng ABC.A’B’C’ có thể tích bằng V. Các điểm M, N, P lần lượt thuộc cạnh AA’, BB’, CC’ sao cho \(\frac{{AM}}{{AA'}} = \frac{1}{2},\,\,\,\frac{N}{{BB'}} = \frac{{CP}}{{CC'}} = \frac{3}{4}\). Thể tích khối đa diện ABC.MNP là:
\(\frac{2}{3}V\)
\(\frac{1}{8}V\)
\(\frac{1}{3}V\)
\(\frac{1}{2}V\)
Tìm nghiệm của phương trình \({\log _x}\left( {4 - 3x} \right) = 2\)
\(x = 1\)
\(x = 4\)
\(x \in \emptyset \)
\(x \in \left( {1; - 4} \right)\)
Với giá trị nào của số thực m thì hàm số \(y = \frac{{x + m}}{{x + 1}}\) đồng biến trên từng khoảng xác định?
\(m < 1\)
\(m \ge 1\)
\(m > 1\)
\(m \le 1\)
Khối cầu có bán kính 3cm thì có thể tích là:
\(9\pi \left( {c{m^3}} \right)\)
\(12\pi \left( {c{m^3}} \right)\)
\(36\pi \left( {c{m^3}} \right)\)
\(27\pi \left( {c{m^3}} \right)\)
Nghiệm của phương trình \({5^{2 - x}} = 125\) là
\(x = - 1\)
\(x = - 5\)
\(x = 3\)
\(x = 1\)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \(ABC = {30^0}\). Tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABC là:
\(\frac{{{a^3}}}{{16}}\)
\(\frac{{3\sqrt 3 {a^3}}}{{16}}\)
\(\frac{{3{a^3}}}{{16}}\)
\(\frac{{\sqrt 3 {a^3}}}{{16}}\)
Gọi \({y_1},\,{y_2}\) lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số \(y = - {x^4} + 10{x^2} - 9\) . Khi đó, \(\left| {{y_1} - {y_2}} \right|\) bằng:
7
\(2\sqrt 5 \)
25
9
Giá trị nhỏ nhất của hàm số \(y = {e^{2x}} + 3{e^x} - 1\) trên đoạn \(\left[ {\ln 2;\ln 5} \right]\) là:
\({e^2}\)
9
\({e^9}\)
39
\({\log _{\frac{1}{a}}}\sqrt[3]{{{a^7}}},\,\,\,a > 0,\,\,a \ne 1\) bằng
\( - \frac{3}{7}\)
\(\frac{7}{3}\)
\(\frac{3}{7}\)
\( - \frac{7}{3}\)
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x - 3}}{{x - 7}}\) có phương trình là:
\(y = 7\)
\(y = 2\)
\(x = 7\)
\(x = 2\)
Cho hàm số \(y = \frac{{3x + 1}}{{x - 1}}\). Chọn khẳng định đúng:
Hàm số nghịch biến trên \(\left( { - \infty ;1} \right) \cup \left( {1; + \infty } \right)\)
Hàm số nghịch biến trên từng khoảng xác định của nó.
Hàm số đồng biến trên R.
Hàm số nghịch biến trên R.
Tập xác định của hàm số \(y = {\left( {2x - 1} \right)^{ - \frac{1}{2}}}\) là
\(\left[ {\frac{1}{2}; + \infty } \right)\)
\(R\backslash \left\{ {\frac{1}{2}} \right\}\)
\(\left( {\frac{1}{2}; + \infty } \right)\)
R