Quiz

Bộ 25 đề thi học kì 1 Toán 12 năm 2022-2023 có đáp án (Đề 19)

VietJackToánLớp 122 lượt thi

50 câu hỏi

Hiển thị đáp án

1. Trắc nghiệm

• 1 điểm • Không giới hạn

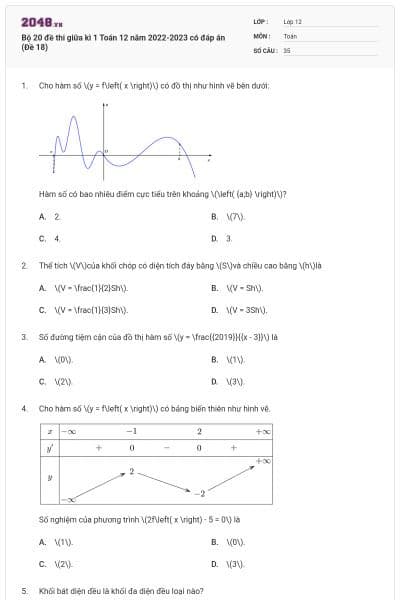
Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê dưới đây. Hỏi hàm số đó là hàm số nào?

Media VietJack

$y = \frac{1}{2} x^{4} - x^{2} - 3$ .

$y = x^{4} - 2 x^{2} - 3$ .

$y = - \frac{1}{2} x^{4} + 2 x^{2} - 3$ .

$y = - x^{4} + 2 x^{2} - 3$ .

Xem đáp án

2. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $f (x) = \log_{\frac{1}{3}} (1 - x^{2})$ . Biết tập nghiệm của bất phương trình $f^{'} (x) > 0$ là khoảng (a;b). Tính S = a +2b.

S = -1

S = 2

S = -2

S = 1

Xem đáp án

3. Trắc nghiệm

• 1 điểm • Không giới hạn

Số mặt phẳng đối xứng của một hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đôi một khác nhau là

Xem đáp án

4. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho a, b là hai số thực dương. Tìm x biết $\log_{3} x = 3 \log_{3} a - 2 \log_{\frac{1}{3}} b$

$x = a^{3} b^{2}$ .

$x = a^{2} b^{3}$ .

$x = \frac{a^{3}}{b^{2}}$ .

$x = 3 a + 2 b$ .

Xem đáp án

5. Trắc nghiệm

• 1 điểm • Không giới hạn

Tính giá trị nhỏ nhất của hàm số $y = \sqrt{4 - x^{2}}$ trên đoạn [-1;1].

$\min_{[- 1; 1]} y = \sqrt{3}$ .

$\min_{[- 1; 1]} y = 0$ .

$\min_{[- 1; 1]} y = 2$ .

$\min_{[- 1; 1]} y = \sqrt{2}$ .

Xem đáp án

6. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho x là số thực dương và biểu thức $P = \sqrt[3]{x^{2} \sqrt[4]{x \sqrt{x}}}$ . Viết biểu thức P dưới dạng lũy thừa của một số với số mũ hữu tỉ.

$P = x^{\frac{1}{432}}$ .

$P = x^{\frac{58}{63}}$ .

$P = x^{\frac{19}{24}}$ .

$P = x^{\frac{1}{4}}$ .

Xem đáp án

7. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh SA vuông góc với mặt phẳng (ABCD), góc giữa cạnh SD và mặt phẳng (ABCD) bằng $60 °$ . Thể tích của khối chóp đã cho bằng:

$\sqrt{3} a^{3}$ .

$\frac{\sqrt{3} a^{3}}{6}$ .

$\frac{\sqrt{3} a^{3}}{3}$ .

$\frac{\sqrt{3} a^{3}}{9}$ .

Xem đáp án

8. Trắc nghiệm

• 1 điểm • Không giới hạn

Giá trị cực tiểu $y_{C T}$ của hàm số $y = x^{3} - 3 x^{2} + 7$ là:

$y_{C T} = 2$ .

$y_{C T} = 3$ .

$y_{C T} = 0$ .

$y_{C T} = 7$ .

Xem đáp án

9. Trắc nghiệm

• 1 điểm • Không giới hạn

Biết rằng năm 2009 dân số Việt Nam là 85.847.000 người và tỉ lệ tăng dân số năm đó là 1,2%. Cho biết sự tăng dân số được ước tính theo công thức $S = A e^{N r}$ (A là dân số năm lấy làm mốc tính; S là dân số sau N năm; r là tỉ lệ tăng dân số hàng năm). Nếu cứ tăng dân số với tỉ lệ như vậy thì sau bao nhiêu năm nữa dân số nước ta ở mức 120 triệu người?

26 năm.

27 năm.

28 năm.

29 năm.

Xem đáp án

10. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho ${(π - 2)}^{m} > {(π - 2)}^{n}$ với m, n là các số nguyên. Khẳng định đúng là:

$m > n$ .

$m \leq n$ .

$m \geq n$ .

$m < n$ .

Xem đáp án

11. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = \frac{1}{3} x^{3} - x^{2} + (m - 1) x + 2019$ . Giá trị nhỏ nhất của tham số m để hàm số đồng biến trên tập xác định là:

m = 2.

m = -2.

$m = \frac{5}{4}$ .

m = 0 .

Xem đáp án

12. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = x^{3} - 3 x^{2}$ . Có bao nhiêu tiếp tuyến của đồ thị hàm số song song với trục hoành?

Xem đáp án

13. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm số giao điểm của đồ thị hàm số $y = (1 - 2 x) (2 x^{2} - 5 x + 2)$ với trục hoành.

Xem đáp án

14. Trắc nghiệm

• 1 điểm • Không giới hạn

Hình hai mươi mặt đều có mỗi đỉnh là đỉnh chung của số cạnh là

Xem đáp án

15. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình vuông cạnh a, hình chiếu vuông góc của A' lên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB, góc giữa A'C và mặt phẳng (ABCD) bằng $45 °$ . Thể tích của khối lăng trụ đã cho bằng

$\frac{\sqrt{5} a^{3}}{2}$ .

$\frac{\sqrt{5} a^{3}}{12}$ .

$\frac{\sqrt{5} a^{3}}{6}$ .

$\frac{3 \sqrt{5} a^{3}}{2}$ .

Xem đáp án

16. Trắc nghiệm

• 1 điểm • Không giới hạn

Hình đa diện có các đỉnh là trung điểm tất cả các cạnh của một tứ diện đều là:

Bát diện đều.

Hình lập phương.

Tứ diện đều.

Thập nhị diện đều.

Xem đáp án

17. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho $\log_{2} 3 = a; \log_{3} 7 = b$ . Biểu diễn $P = \log_{21} 126$ theo a, b.

$P = \frac{a b + 2 a + 1}{a b + a}$ . B. $P = \frac{a b + 2 a + 1}{a b + 1}$ . C. $P = \frac{a b + 2 a + 1}{b + 1}$ . D. $P = \frac{a + b + 2}{b + 1}$ .

$P = \frac{a b + 2 a + 1}{a b + 1}$ .

$P = \frac{a b + 2 a + 1}{b + 1}$ .

$P = \frac{a + b + 2}{b + 1}$ .

Xem đáp án

18. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các khẳng định sau, tìm khẳng định sai.

Hàm số y = log x đồng biến trên R.

Hàm số $y = π^{- x}$ nghịch biến trên R.

Hàm số $y = x^{π}$ đồng biến trên $(0; + \infty)$ .

Hàm số $y = e^{x}$ đồng biến trên R.

Xem đáp án

19. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $\frac{2 x + 1}{x - 2}$ . Tìm khẳng định sai.

Đồ thị hàm số có hai đường tiệm cận.

Hàm số nghịch biến trên từng khoảng xác định.

$\lim_{x \to 2^{-}} = + \infty; \lim_{x \to 2^{+}} y = - \infty$ .

Hàm số không có cực trị.

Xem đáp án

20. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Gọi M là trung điểm của SA. Tính thể tích của khối chóp M.ABC bằng:

$\frac{\sqrt{13} a^{3}}{12}$ .

$\frac{\sqrt{11} a^{3}}{48}$ .

$\frac{\sqrt{11} a^{3}}{8}$ .

$\frac{\sqrt{11} a^{3}}{24}$ .

Xem đáp án

21. Trắc nghiệm

• 1 điểm • Không giới hạn

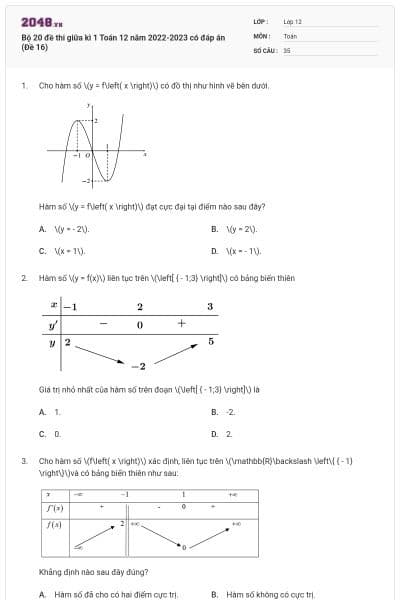
Cho hàm số $y = \frac{a x + b}{c x + d}$ có đồ thị như hình vẽ bên

Media VietJack

Khẳng định nào dưới đây là khẳng định đúng?

$a b < 0; a c > 0; b d > 0$ .

$a b > 0; a c > 0; b d > 0$ .

$a b < 0; a c > 0; b d < 0$ .

$a b > 0; a c < 0; b d > 0$ .

Xem đáp án

22. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định của hàm số $y = \log (x^{3} - 3 x + 2)$

$D = (- 2; + \infty)$ .

$D = (- 2; + \infty) \ \{1\}$ .

$D = [- 2; + \infty) \ \{1\}$ .

$D = (- \infty; - 2) \cup (1; + \infty)$

Xem đáp án

23. Trắc nghiệm

• 1 điểm • Không giới hạn

Đồ thị hàm số $y = \frac{x - 1}{\sqrt{3 x^{2} + 1}}$ có bao nhiêu đường tiệm cận ngang?

Xem đáp án

24. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong không gian cho hai điểm phân biệt A, B cố định. Tập hợp các điểm M thỏa mãn đẳng thức $\vec{M A} . \vec{M B} = 0$ là:

Mặt cầu bán kính AB.

Hình tròn bán kính AB.

Mặt cầu đường kính AB.

Hình tròn đường kính AB.

Xem đáp án

25. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho $0 < a \neq 1; 0 < b \neq 1$ và x, y là hai số thực dương. Mệnh đề nào dưới đây đúng?

$\log_{a} \frac{x}{y} = \frac{\log_{a} x}{\log_{a} y}$ .

$\log_{a}^{2} (x y) = \log_{a}^{2} x + \log_{a}^{2} y$ .

$\log_{a} \frac{1}{x} = \frac{1}{\log_{a} x}$ .

$\log_{b} x = \log_{a} x^{\log_{b} a}$ .

Xem đáp án

26. Trắc nghiệm

• 1 điểm • Không giới hạn

Tính đạo hàm của hàm số $y = 2^{x^{2} - \sin x + 2}$

$y^{'} = (2 x - \cos x) 2^{x^{2} - \sin x + 2} \ln 2$ .

$y^{'} = 2^{x^{2} - \sin x + 2} \ln 2$ .

$y^{'} = (x^{2} - \sin x + 2) 2^{x^{2} - \sin x + 2}$ .

$y^{'} = (2 x - \cos x) 2^{x^{2} - \sin x + 2}$ .

Xem đáp án

27. Trắc nghiệm

• 1 điểm • Không giới hạn

Thể tích của khối cầu đường kính 3R bằng:

$\frac{9 π R^{3}}{8}$ .

$\frac{27 π R^{3}}{8}$ .

$\frac{9 π R^{3}}{2}$ .

$36 π R^{3}$ .

Xem đáp án

28. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, cạnh SA vuông góc với mặt phẳng (ABC), $B C = a, S A = A B$ . Thể tích của khối chóp đã cho bằng:

$\frac{\sqrt{2} a^{3}}{24}$ .

$\frac{\sqrt{2} a^{3}}{8}$ .

$\frac{\sqrt{3} a^{3}}{24}$ .

$\frac{\sqrt{3} a^{3}}{8}$ .

Xem đáp án

29. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y = 4 x^{3} + m x^{2} - 12 x + 5$ đạt cực tiểu tại điểm x =-2.

Không tồn tại giá trị của m.

$m = \frac{3}{4}$ .

m =0.

m =9.

Xem đáp án

30. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = - x^{3} + 3 x^{2} + 2$ . Tìm phương trình tiếp tuyến của đồ thị hàm số tại tâm đối xứng của đồ thị.

$y = 3 x + 1$ .

$y = 3 x - 1$ .

$y = - 3 x + 1$ .

$y = - 3 x - 1$ .

Xem đáp án

31. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = \frac{2 x + 1}{x - 1}$ . Khẳng định nào sau đây là đúng?

Hàm số nghịch biến trên các khoảng $(- \infty; 1)$ và $(1; + \infty)$ .

Hàm số đồng biến trên các khoảng $(- \infty; 1)$ và $(1; + \infty)$ .

Hàm số nghịch biến trên $(- \infty; 1) \cup (1; + \infty)$ .

Hàm số nghịch biến trên $ℝ \ \{1\}$ .

Xem đáp án

32. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hình chóp tứ giác sau, hình chóp nào có mặt cầu ngoại tiếp:

Hình chóp có đáy là hình thang vuông.

Hình chóp có đáy là hình thang cân.

Hình chóp có đáy là hình bình hành.

Hình chóp có đáy là hình thang.

Xem đáp án

33. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho a, b là các số thực dương, m là một số nguyên và n là một số nguyên dương. Tìm khẳng định sai.

$a^{\frac{m}{n}} = \sqrt[n]{a^{m}}$ .

$a^{\frac{m}{n}} = \sqrt[m]{a^{n}}$ .

$\frac{a^{m}}{b^{m}} = {(\frac{a}{b})}^{m}$ .

${(a b)}^{m} = a^{m} b^{m}$ .

Xem đáp án

34. Trắc nghiệm

• 1 điểm • Không giới hạn

Đồ thị hàm số nào sau đây có tiệm cận đứng là đường thẳng x =-2?

$y = \frac{x + 1}{x^{2} - 4}$ .

$y = \frac{x + 2}{x^{2} - 4}$

$y = \frac{x + 2}{x^{2} + 4}$

$y = \frac{x + 1}{x^{2} + 4}$

Xem đáp án

35. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp đều S.ABCD có cạnh đáy bằng 4cm và chiều cao bằng 2cm. Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng

4,5cm.

3cm.

6cm.

4cm.

Xem đáp án

36. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối tứ diện ABCD có thể tích bằng V. Gọi M là trung điểm cạnh AB, N thuộc cạnh AC sao cho AN =2NC, P thuộc cạnh AD sao cho PD =2AP. Thể tích của khối đa diện MNP.BCD tính theo V là:

$\frac{21}{24} V$ .

$\frac{5}{6} V$ .

$\frac{7}{8} V$ .

$\frac{11}{12} V$ .

Xem đáp án

37. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số y= f(x) xác định và liên tục trên R và có bảng biến thiên như hình vẽ.

Cho hàm số y =f(x) xác định và liên tục trên R và có bảng biến thiên như hình vẽ.Khẳng định nào sau đây đúng? (ảnh 1)

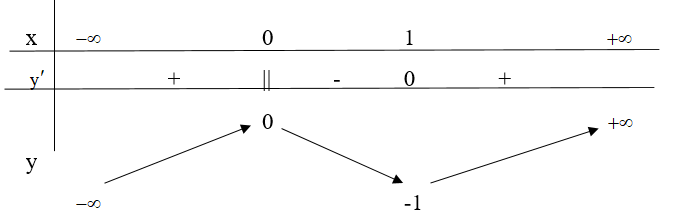
Khẳng định nào sau đây đúng?

Hàm số đạt cựa tiểu tại x = 1.

Hàm số đạt giá trị lớn nhất bằng 0, giá trị nhỏ nhất bằng -1.

Hàm số có giá trị cực tiểu bằng 1.

Hàm số có một cực trị.

Xem đáp án

38. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = x^{4} - 2 x^{2} + 1$ . Tìm khẳng định sai?

Hàm số đạt cực đại tại x =0.

Đồ thị hàm số nhận gốc tọa độ làm tâm đối xứng.

Đồ thị hàm số nhận trục tung làm trục đối xứng.

$\lim_{x \to - \infty} = + \infty$ .

Xem đáp án

39. Trắc nghiệm

• 1 điểm • Không giới hạn

Số điểm cực trị của hàm số $y = - 2 x^{4} - x^{2} + 5$ là

Xem đáp án

40. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm điều kiện của tham số m để phương trình $2 x^{3} - 3 x^{2} - 2 m - 1 = 0$ có ba nghiệm phân biệt.

$- 1 < m < - \frac{1}{2}$

$0 < m < \frac{1}{2}$

$- 1 \leq m \leq - \frac{1}{2}$

$- \frac{1}{2} < m < 0$

Xem đáp án

41. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = - \frac{1}{3} x^{3} - 2 x^{2} + 1$ đồng biến trên khoảng nào dưới đây?

$(- 4; 0)$ .

$(- \infty; - 4)$ .

$(0; + \infty)$ .

Xem đáp án

42. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số nào dưới đây có giá trị lớn nhất trên R?

$y = x^{4} - 2 x^{2}$ .

$y = - 3 x^{3} + x^{2} - 5$ .

$y = x^{3} + 3 x^{2} - 7 x + 1$

$y = - 2 x^{4} - x^{2} + 5$

Xem đáp án

43. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, BC =a, $A C B = 30 °$ . Mặt bên AA'B'B là hình vuông. Diện tích xung quanh của hình lăng trụ đã cho là:

$\frac{(3 + 2 \sqrt{3}) a^{2}}{3}$

$(3 + \sqrt{3}) a^{2}$

$\frac{(3 + \sqrt{3}) a^{2}}{3}$

$\frac{(6 + 3 \sqrt{3}) a^{2}}{6}$

Xem đáp án

44. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = x^{3} + (m^{2} + 1) x + m^{2} - 2$ . Tìm số thực dương m để hàm số có giá trị nhỏ nhất trên đoạn [0;2] bằng 2.

m = 2

m =4

m =1

m =0

Xem đáp án

45. Trắc nghiệm

• 1 điểm • Không giới hạn

Một chất điểm chuyển động có phương trình $S (t) = - \frac{1}{3} t^{3} + 6 t^{2}$ với thời gian t tính bằng giây (s) và quãng đường S tính bằng mét (m). Trong thời gian 5 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của chất điểm đạt được là

35 m/s

36m/s.

288 m/s.

$\frac{325}{3}$ m/s.

Xem đáp án

46. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA =a, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60o. Biết mặt cầu tâm A bán kính $\frac{a \sqrt{3}}{2}$ cắt mặt phẳng (SBC) theo giao tuyến là một đường tròn. Bán kính của đường tròn giao tuyến đó bằng:

$\frac{\sqrt{2} a}{2}$

$\frac{\sqrt{5} a}{2}$

$\frac{\sqrt{3} a}{2}$

$\frac{a}{2}$

Xem đáp án

47. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số f(x), hàm số y =f'(x) liên tục trên R và có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số $g (x) = f (x^{2} + x)$ là:

Media VietJack

Xem đáp án

48. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật. $A D = 3 A B = 3 a$ , SA vuông góc với mặt phẳng (ABCD), SA =a.Gọi M là trung điểm của BC, DM cắt AC tại I (minh họa như hình vẽ bên). Thể tích của khối chóp S.ABMI bằng:

Media VietJack

$\frac{21 a^{3}}{16}$ .

$\frac{7 a^{3}}{18}$ .

$\frac{7 a^{3}}{16}$ .

$\frac{5 a^{3}}{12}$ .

Xem đáp án

49. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $f (x) = \ln \frac{2020 x}{x + 1}$ . Tính tổng $S = f^{'} (1) + f^{'} (2) + f^{'} (3) + ... + f^{'} (2020)$

$S = \frac{2018}{2019}$ .

S =2020.

$S = \frac{2020}{2021}$ .

$S = \frac{2019}{2020}$ .

Xem đáp án

50. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình hộp chữ nhật ABCD.A'B'C'D'thay đổi nhưng luôn nội tiếp một hình cầu cố định có bán kính R. Biết $A B = 2 A D = 2 x (x > 0)$ . Tìm x để thể tích khối hộp đã cho đạt giá trị lớn nhất.