Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án- Đề 5
39 câu hỏi
Cho hàm số có bảng biến thiên như sau:
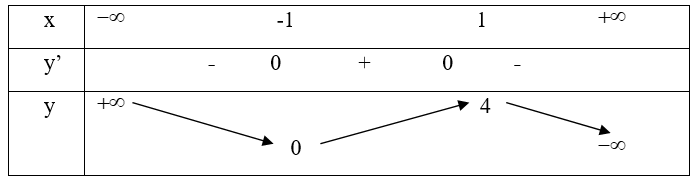
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Cho hàm số y=f(x) có đồ thị là đường cong trong hình sau. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Cho hàm số có đạo hàm Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Cho hàm số y=f(x) có bảng biến thiên như sau:
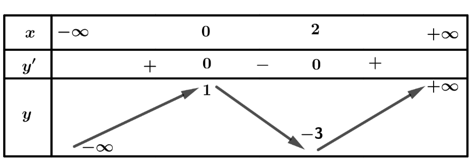
Mệnh đề nào dưới đây đúng?
Hàm số đạt cực tiểu tại
Hàm số đạt cực tiểu tại x=2
Hàm số đạt cực tiểu tại x=-3
Hàm số đạt cực tiểu tại x=0
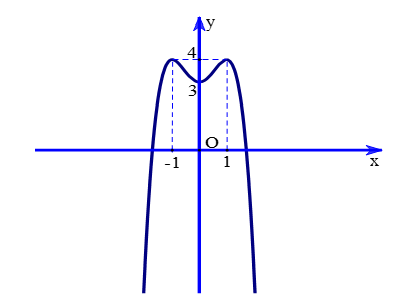
Cho hàm số y= f(x) có đồ thị như hình vẽ bên.
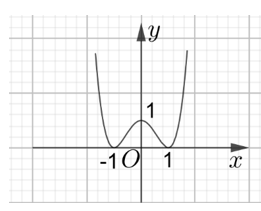
Số điểm cực trị của đồ thị hàm số y=f(x) là
3
2
0
1
Cho hàm số y= f(x) có bảng xét dấu của như sau:

Mệnh đề nào dưới đây đúng?
Hàm số có ba điểm cực đại.
Hàm số có hai điểm cực đại.
Hàm số có một điểm cực đại.
Hàm số không có điểm cực đại.
Cho hàm số liên tục trên R và có bảng xét dấu như sau
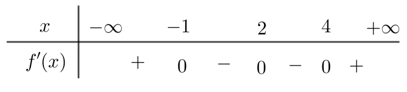
Hàm số có bao nhiêu điểm cực trị?
0
1
2
3
Hàm số liên tục và có bảng biến thiên trong đoạn cho trong hình bên. Gọi M là giá trị lớn nhất của hàm số trên đoạn . Tìm mệnh đề đúng?
Cho hàm số có đồ thị như hình vẽ.
![Cho hàm số y=f(x) có đồ thị như hình vẽ. Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [0,3] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/02/blobid0-1675860608.png)
Giá trị nhỏ nhất của hàm số trên đoạn bằng
0
2
3
-4
Đường cong ở hình bên là đồ thị của hàm số nào dưới đây?
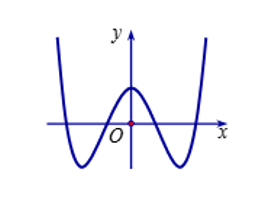
Đường cong ở hình bên dưới là đồ thị của hàm số nào dưới đây?
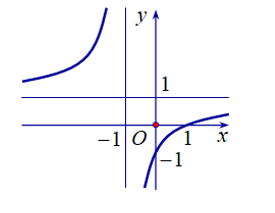
Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
x= 1và y= -3
x= 2 và y=1
x=1 và y=2
x=-1 và y=2
Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số ?
x=-1
y=-1
y=2
x=1
Cho hàm số y= f(x) có và . Khẳng định nào sau đây là khẳng định đúng?
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x=1và x=-1
Đồ thị hàm số đã cho không có tiệm cận ngang.
Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y= 1và y=-1 .
Cho các hình sau:
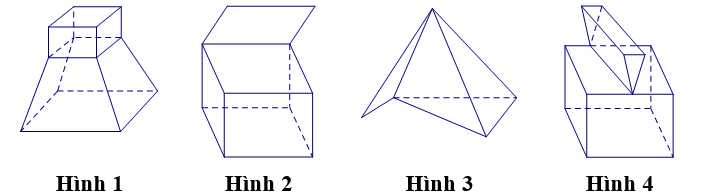
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
Hình 1.
Hình 2
Hình 3.
Hình 4.
Hình đa diện nào không có tâm đối xứng?
Hình bát diện đều.
Hình tứ diện đều.
Hình lập phương.
Hình lăng trụ tứ giác đều
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA= . Tính thể tích của khối chóp.
Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3 . Thể tích khối lăng trụ đã cho bằng
Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là
3Bh
Bh
Tính thể tích chóp biết chiều cao là 3a, diện tích đáy .
Cho hàm số có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng nào dưới đây?
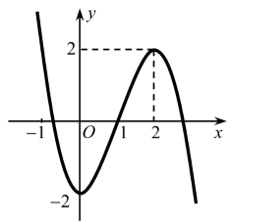
Cho hàm số Mệnh đề nào sau đây đúng?
Hàm số nghịch biến trên khoảng
Hàm số đồng biến trên các khoảng và , nghịch biến trên khoảng
Hàm số đồng biến trên khoảng , ngịch biến trên các khoảng và
Hàm số đồng biến trên các khoảng và, nghịch biến trên khoảng
Cho hàm số y=f(x) xác định và có đạo hàm cấp một và cấp hai trên khoảng (a,b) và Khẳng định nào sau đây sai?
Nếu thì là điểm cực trị của hàm số.
Nếu và thì là điểm cực tiểu của hàm số.
Nếu và thìlà điểm cực trị của hàm số.
Nếu hàm số đạt cực đại tại thì
Cho hàm số xác định, liên tục trên R và có bảng biến thiên
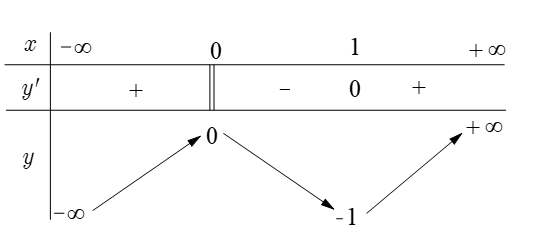
Khẳng định nào sau đây đúng?
Hàm số không có điểm cực trị.
Hàm số có đúng một cực trị.
Hàm số có giá trị cực tiểu bằng .
Hàm số đạt cực đại tại và đạt cực tiểu tại .
Trên khoảng hàm số .
Có giá trị nhỏ nhất là .
Có giá trị lớn nhất là .
Có giá trị nhỏ nhất là .
Có giá trị lớn nhất là .
Giá trị lớn nhất của hàm số trên đoạn bằng:
-16
20
0
4
Đường cong sau đây là đồ thị của hàm số nào?
Cho hàm số có đồ thị như hình vẽ bên dưới. Với giá trị nào của m thì phương trình có 2 nghiệm phân biệt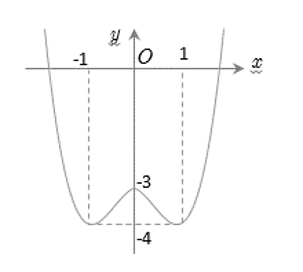
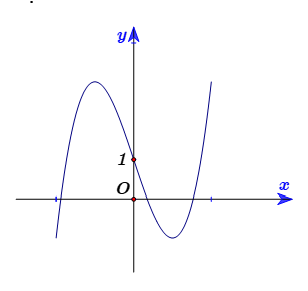
Cho hàm số bậc ba có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình là:
3
1
0
2
Tiệm cận ngang của đồ thị hàm số là:
Đồ thị hàm số có tất cả bao nhiêu tiệm cận?
1
2
3
4
Khẳng định nào sau đây là đúng khi nói về số cạnh của hình đa diện đều.
Lớn hơn 6.
Lớn hơn hoặc bằng 6.
Lớn hơn 7.
Lớn hơn hoặc bằng 8.
Trong các mệnh đề sau, mệnh đề nào sai?
Tồn tại hình đa diện đều mà các mặt của nó là những tam giác đều.
Tồn tại hình đa diện đều mà các mặt của nó là những hình vuông.
Tồn tại hình đa diện đều mà các mặt của nó là những ngũ giác đều.
Tồn tại hình đa diện đều mà các mặt của nó là những lục giác đều.
Cho hình chóp SABCD có SA ( ABCD), đáy ABCD là hình chữ nhật. Tính thể tích SABCD biết AB=a, AD=2a , SA=3a.
Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng là:
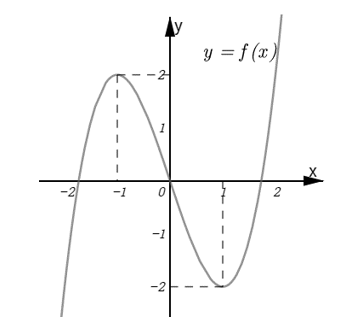
Cho hàm số f(x) . Hàm số y=f'(x) có đồ thị như hình bên. Hàm số g(x)=(1-2x)+-x nghịch biến trên khoảng nào ?
Cho lăng trụ ABCA'B'C'có chiều cao bằng 4 và đáy là tam giác đều cạnh bằng 4. Gọi M, N và P lần lượt là tâm của các mặt bên ABB'A', ACC'A' và BCC'B'. Thể tích của khối đa diện lồi có các đỉnh là các điểm A,B,C, M,N, P bằng?
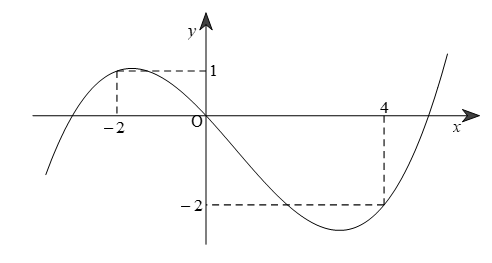
Cho hàm số y=f'(x-1) có đồ thị như hình vẽ: Tìm điểm cực tiểu của hàm số y=2f(x)-4x .
Cho hàm số . Tìm m để .