Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án- Đề 19
50 câu hỏi
Cho hàm số xác định, liên tục trên R và có bảng biến thiên như hình vẽ:
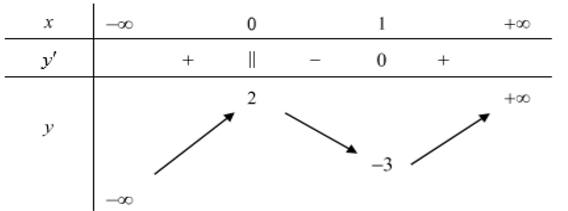
Mệnh đề nào sau đây ĐÚNG?
Hàm số có hai điểm cực trị.
Hàm số có giá trị lớn nhất bằng và giá trị nhỏ nhất bằng
Hàm số chỉ có giá trị nhỏ nhất, không có giá trị lớn nhất.
Hàm số có một điểm cực trị.
Hàm số có điểm cực tiểu là:
x =0
x = 1
x = 5
x = -1
Cho hàm số y =f(x) có bảng biến thiên như sau:
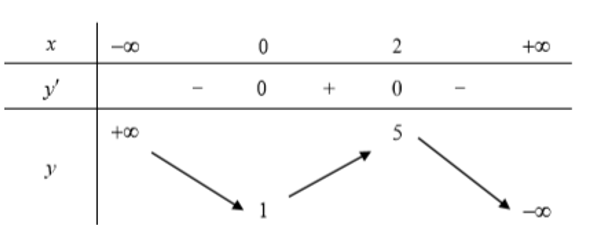 Hàm số đạt cực tiểu tại điểm
Hàm số đạt cực tiểu tại điểm
x = 0
y = 1
M(2;5)
x = 2
Cho hàm số có đồ thị như hình vẽ. Đồ thị hàm số y =f(x) có bao nhiêu cực trị?
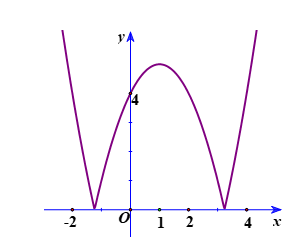
4
2
1
3
Tìm giá trị thực của tham số m để đường thẳng vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
Cho hàm số y =f(x) có và Khẳng định nào sau đây là khẳng định đúng?
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y =1 và y =-1
Đồ thị hàm số đã cho không có hai tiệm cận ngang.
Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x =1 và x =-1
Xét các khẳng định sau:
(I) Nếu hàm số y =f(x) có giá trị cực đại là M và giá trị cực tiểu là m thì
(II) Đồ thị hàm số luôn có ít nhất một điểm cực trị.
(III)Tiếp tuyến (nếu có) tại điểm cực trị của đồ thị hàm số luôn song song với trục hoành.
Số khẳng định đúng là
3
1
0
2
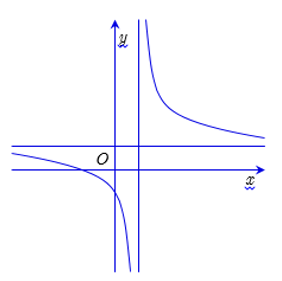
Đồ thị của hàm số nào dưới đây có đường tiệm cận ngang?
.
.
.
.
Cho hàm số y =f(x) xác định, liên tục có đạo hàm trên đoạn (với ). Xét các khẳng định sau:
(I). Nếu thì hàm số y =f(x) đồng biến trên khoảng (a;b).
(II). Giả sử suy ra hàm số nghich biến trên (a;b).
(III). Giả sử phương trình có nghiệm x =m. Khi đó nếu hàm số f(x) đồng biến trên (m;b) thì hàm số f(x) nghịch biến trên (a;m).
(IV). Nếu hàm số y =f(x) đồng biến trên khoảng (a;b) thì
Số mệnh đề đúng trong các mệnh đề trên là:
3
1
0
2
Có bao nhiêu giá trị nguyên không âm của tham số m sao cho hàm số đồng biến trên khoảng
4
5
3
6
Cho hàm số y =f(x) Hàm số y =f'(x) có đồ thị như hình bên.
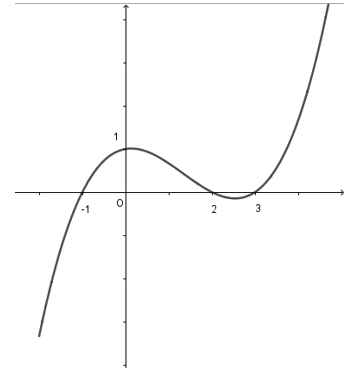
Hàm số đồng biến trên khoảng
(-2;0)
(2;3)
Tìm giá trị thực của hàm số m để hàm số đạt cực đại tại x =3
m =-1
m = 5
m = 1
m =-7
Tìm tất cả các giá trị của tham số m để hàm số có cực đại và cực tiểu.
.
.
.
.
Cho hàm số có đồ thị như hình vẽ, xác định dấu của a,b,c.
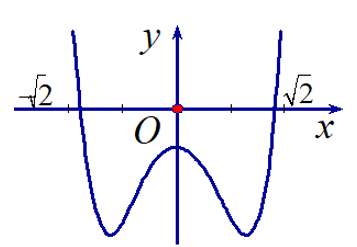
.
.
.
.
Hàm số nghịch biến trên mỗi khoảng nào sau đây?
.
.
.
.
Tìm tất cả các giá trị m để hàm số nghịch biến trên R.
.
.
.
Gọi S là tập hợp tất cả các giá trị m sao cho giá trị lớn nhất của hàm số trên đoạn [-3;3] bằng7. Số phần tử của S là :
2
0
6
1
Cho hàm số y =f(x) xác định và liên tục trên khoảng và . Đồ thị hàm số y =f(x) là đường cong như hình vẽ bên :
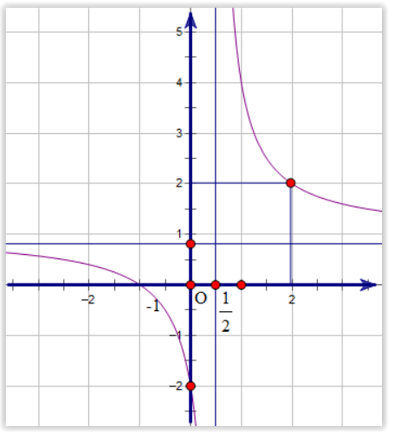
Tìm mệnh đề đúng trong các mệnh đề sau :
.
.
.
Cho hàm số y =f(x) có đồ thị của hàm số y=f'(x) như hình vẽ.
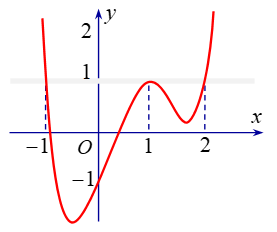
Khi đó hàm số có bao nhiêu điểm cực trị ?
1
4
3
2
Tìm m ể tiệm cận ngang của đồ thị của hàm số cắt đường thẳng tại điểm có hoành độ bằng 2.
m =2
m =1
m =10
m =7
Có bao nhiêu giá trị của tham số m thỏa mãn đồ thị hàm số có đúng hai đường tiệm cận ?
3
1
4
2
Hàm số có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
Cho hàm số y =f(x). Hàm số y =f'(x) có đồ thị như hình vẽ dưới đây. Hàm số đồng biến trên khoảng
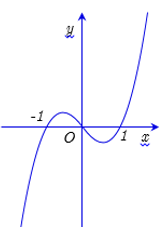
(0;1)
(-1;1)
Tìm tất cả các tiệm cận đứng của đồ thị hàm số
x =-3 và x =-2
x =-3
x = 3 và x = 2
x = 3
Cho hàm số y =f(x) xác định, liên tục trên và có bảng biến thiên sau
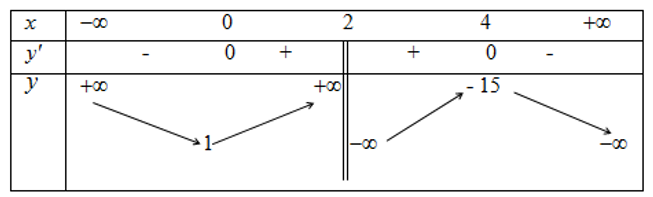
Khẳng định nào sau đây là khẳng định sai?
Đồ thị hàm số không có tiệm cận ngang.
Hàm số đạt cực tiểu tại x =0 và đạt cực đại tại x = 4
Đồ thị hàm số có tiệm cận đứng là đường thẳng x = 2
Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng -15.
Cho khối chóp có đáy là đa giác lồi có 7 cạnh. Trong số các mệnh đề sau, mệnh đề nào đúng?
Số cạnh của khối chóp bằng 8.
Số cạnh của khối chóp bằng 14.
Số mặt của khối chóp bằng số đỉnh của nó.
Số đỉnh của khối chóp bằng 15
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a. Cạnh SA vuông góc với mặt phẳng đáy và có độ dài là a. Thể tích khối tứ diện SBCD bằng
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A. Biết rằng Tính thể tích khối lăng trụ ABC.A'B'C' là
20
30
60
10
Cho tứ diện ABCD có ABC là tam giác vuông cân tại C và nằm trong mặt phẳng vuông góc với mặt phẳng (ABD) tam giác ABD là tam giác đều
và có cạnh bằng 2a. Tính thể tích của khối tứ diện ABCD
Hình đa diện sau có bao nhiêu cạnh?
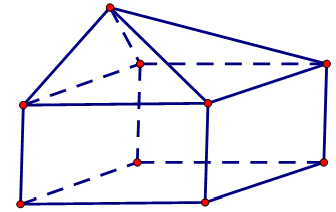
12
16
8
9
Hình chóp SABCD, đáy là hình chữ nhật có: SA vuông góc với mặt phẳng đáy, . Thể tích của khối chóp SABCD là:
Hình vẽ bên dưới có bao nhiêu mặt
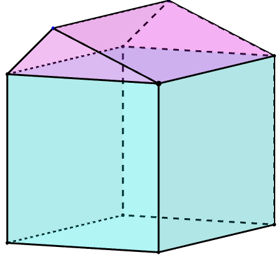
10
7
9
4
Lắp ghép hai khối đa diện , để tạo thành khối đa diện (H), trong đó là khối chóp tứ giác đều có tất cả các cạnh bằng a, là khối tứ diện đều cạnh a sao cho một mặt của trùng với một mặt của như hình vẽ. Hỏi khối đa diện (H) có tất cả bao nhiêu mặt?
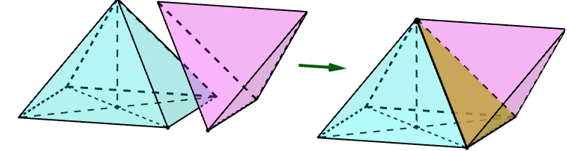
9
7
8
5
Mặt phẳng ( AB'C') chia khối lăng trụ ABCA'B'C' thành các khối đa diện nào?
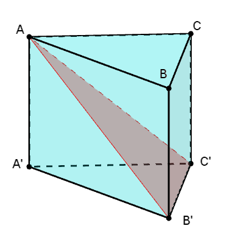
Hai khối chóp tứ giác.
Hai khối chóp tam giác.
Một khối chóp tam giác và một khối chóp ngũ giác.
Một khối chóp tam giác và một khối chóp tứ giác.
Nếu chiều cao và cạnh đáy của một hình chóp tứ giác đều cùng tăng lên 3 lần thì thể tích của nó cũng tăng lên
18 lần.
27 lần.
54 lần.
9 lần
Thể tích hình chóp tứ giác đều có tất cả các cạnh bằng a bằng
Tính thể tích của khối chóp SABC có AB=a, AC=2a, ( SAB) và ( SAC) cùng vuông góc với ( ABC), góc giữa mặt phẳng và là
Cho hình lăng trụ tam giác đều ABCDA'B'C'D' có cạnh đáy bằng a Góc giữa đường thẳng A'B và mặt phẳng (ABC) là 45 Tính thể tích của khối lăng trụ
Cho khối lăng trụ có diện tích đáy bằng S chiều cao bằng h và thể tích bằng V. Trong các đẳng thức dưới đây, hãy tìm đẳng thức đúng ?
Thể tích hình lập phương cạnh là:
3
Cho hình chóp SABCD có đáy hình vuông, cạnh bên SA vuông góc với đáy. Gọi M,N là trung điểm của . Mặt phẳng chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần và là
1
Tính thể tích V của khối hộp chữ nhật có đáy là hình vuông cạnh bằng 6 và chiều cao bằng 5 .
Cho khối chóp trên ba cạnh lần lượt lấy ba điểm sao cho Gọi V và lần lượt là thể tích của các khối chóp SABC và Khi đó tỉ số là:
24
12
Cho hình chóp SABCD có đáy là hình vuông cạnh hình chiếu vuông góc H của S lên mặt phẳng là trung điểm đoạn AB Tính chiều cao của khối chóp HSBD theo a
Cho hình chóp SABCD có đáy là tam giác ABC vuông tại B có AB=3,BC=4 Biết rằng các mặt bên của khối chóp đều tạo với đáy một góc bằng nhau và bằng với đồng thời chân đường cao của hình chóp nằm ở miền trong Thể tích khối chóp đã cho là
Cho hình lăng trụ ABCDA'B'C'D' có đáy ABCD là hình thoi cạnh a tâm O và Góc giữa cạnh bên AA' và mặt đáy bằng 60 Đỉnh A' cách đều các điểm A,B,D Tính theo a thể tích V của hình lăng trụ đã cho.
Cho hình chóp SABCD có đáyABCD là hình chữ nhật với AB=4 cạnh bên SA vuông góc với mặt phẳng đáy ( ABCD) và SC =6 Tính thể tích lớn nhất của khối chóp đã cho.
Cho khối lăng trụ ABCA'B'C'. Gọi P là trọng tâm tam giác A'B'C' và Q là trung điểm của BC. Tính tỉ số thể tích giữa hai khối tứ diện B'PAQ và
Cho hình lăng trụ đứng có và góc bằng Gọi K, I lần lượt là trung điểm các cạnh Tính khoảng cách từ điểm I đến mặt phẳng
Cho hình lăng trụ ABCA'B'C' có đáy ABC là tam giác đều cạnh a, . Biết rằng hình chiếu vuông góc của A' lên là trung điểm của BC. Tính thể tích khối lăng trụ đó.