Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án- Đề 18
50 câu hỏi
Tìm giá trị nhỏ nhất của hàm số trên đoạn .
Cho hàm số liên tục trên R và có đạo hàm Hỏi hàm số có bao nhiêu điểm cực trị?
3
5
4
2
Cho hàm số liên tục trên R . Hàm số có đồ thị như hình vẽ:
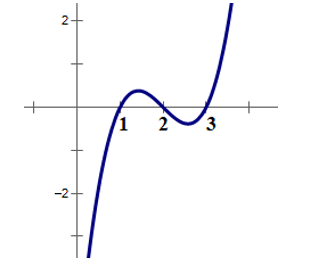
Khẳng định nào sau đây ĐÚNG?
Đồ thị hàm số có 1 điểm cực trị.
Đồ thị hàm số có 2 điểm cực trị.
Đồ thị hàm số có 4 điểm cực trị.
Đồ thị hàm số có 3 điểm cực trị.
Số đường tiệm cận của đồ thị hàm số là:
4
1
3
2
Tìm giá trị lớn nhất của hàm số trên đoạn .
Cho hàm số . Khẳng định nào sau đây là ĐÚNG?
Hàm số nghịch biến trên khoảng và đồng biến trên khoảng .
Hàm số đồng biến trên khoảng và nghịch biến trên khoảng .
Hàm số luôn đồng biến trên R .
Hàm số luôn nghịch biến trên R .
Điểm cực tiểu của đồ thị hàm số là điểm . Tính tổng
Tổng các giá trị nhỏ nhất và giá trị lớn nhất của hàm số bằng
1
2
Tìm tất cả các giá trị thực của tham số m sao cho hàm số luôn nghịch biến trên R
Số đường tiệm cận đứng của đồ thị hàm số là:
2
3
0
1
Hàm số nghịch biến trong khoảng nào?
Cho hàm số có bảng biến thiên dưới đây. Khẳng định nào sau đây là đúng?
Hàm số đạt cực đại tại x=2 .
Hàm số đạt cực đại tại x=3.
Hàm số đạt cực đại tại x=4
Hàm số đạt cực đại tại x=-2
Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
x=2 và y=1
x=-1 và y=2
x=1 và y=2
x=1 và y=-3
Giả sử M ,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên . Khi đó bằng bao nhiêu ?
10
12
Cho hàm số y=f(x) có bảng biến thiên dưới đây. Khẳng định nào sau đây là khẳng định sai?
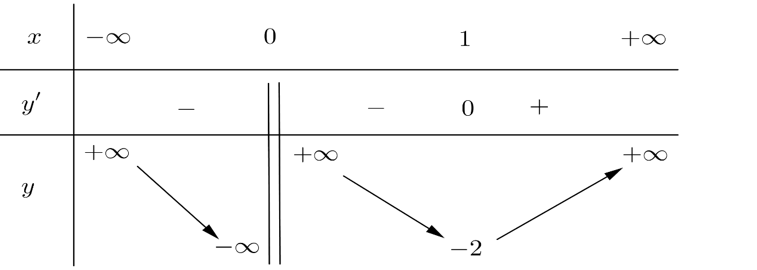
Hàm số đồng biến trên khoảng
Hàm số nghịch biến trên khoảng
Hàm số đồng biến trên khoảng
Hàm số nghịch biến trên khoảng
Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên tập hợp . Tính giá trị ?
Gọi S là tập hợp các giá trị nguyên của tham số m sao cho hàm số nghịch biến trên khoảng . Tính tổng của các m giá trị của S .
P=-10
P=10
Cho hàm số có đạo hàm liên tục trên R . Bảng biến thiên của hàm số được cho như hình vẽ.
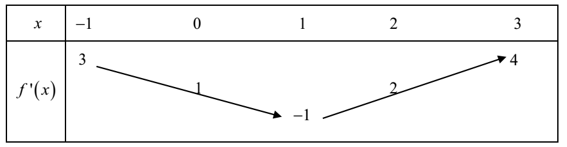
Hàm số nghịch biến trên khoảng nào ?
Có bao nhiêu giá trị nguyên sao cho đồ thị của hàm số có hai tiệm cận ngang.
2
0
3
1
Có bao nhiêu giá trị nguyên của tham số m để hàm số luôn nghịch biến trên từng khoảng xác định của hàm số.
1
3
vô số
2
Gọi S là tập giá trị m là các số nguyên để hàm số đạt cực trị tại hai điểm thỏa mãn Tính tổng P của các giá trị nguyên của
P=1
P=-5
P=-4
Một ngọn hải đăng đặt tại vị trí A có khoảng cách đến bờ biển Trên bờ biển có một cái kho ở vị trí C cách B một khoảng Người canh hải đăng có thể chèo đò từ A đến M vị trí trên bờ biển với vận tốc rồi đi bộ đến C với vận tốc Vị trí điểm M cách B một khoảng bao nhiêu để người đó đi đến kho nhanh nhất ? ( xem hình vẽ).
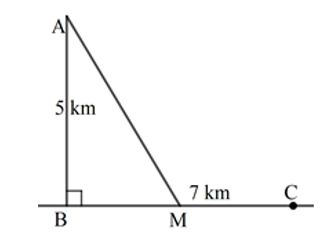
7km
Đồ thị hàm số có tọa độ điểm cực tiểu là . Khi đó bằng
3
4
2
1
Có bao nhiêu giá trị của m để đồ thị hàm số không có tiệm cận đứng
1
0
3
2
Tìm mối liên hệ giữa các tham số a và b sao cho hàm số luôn tăng trên R ?
Một hình chóp có 100 cạnh có bao nhiêu mặt?
50
53
51
52
Cho khối chóp có thể tích và diện tích đáy . Tính chiều cao của khối chóp
Cho hình chóp tứ giác đều SABCD đáy là hình vuông cạnh a cạnh bên hớp với đáy một góc 60 . Gọi M là trung điểm của SC Mặt phẳng qua A,M và song song với BD cắt SB, SD lần lượt tại E và F và chia khối chóp SABCD là hai phần, khối chóp SAEFMF và đa diện . Tính thể tích của khối đa diện ?
Cho hình hộp chữ nhật , có . Tính thể tích của khối chóp ?
Cho hình chóp đều SABC có cạnh đáy bằng a, cạnh bên bằng . Tính theo a thể tích V của khối chóp đã cho
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B và AB= BC= a. Cạnh bên SA= 2a và vuông góc với mặt phẳng đáy. Tính theo a thể tích V của khối chóp SABC
Số đỉnh của hình bát diện đều là bao nhiêu.
10
12
6
8
Kim tự tháp Kheops ( Kê-Ốp ) ở Ai Cập được xây dựng vào năm 2500 trước công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 147m , cạnh đáy dài 230m, . Tính thể tích của nó.
Một khúc gỗ dạng hình hộp chữ nhật có các kích thước như hình vẽ. Người ta cắt đi một phần khúc gỗ có dạng hình lập phương cạnh bằng 4cm . Tính thể tích phần gỗ còn lại.
Tính thể tích V của khối lăng trụ tam giác đều có cạnh đáy bằng a và tổng diện tích các mặt bên bằng
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA = 3a, SA vuông góc với đáy, SB tạo với mặt đáy một góc bằng 60. Tính thể tích khối chóp S.ABC
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Gọi M là trung điểm SB, N là điểm trên đoạn SC sao cho NS = 2NC. Tính thể tích V của khối chóp ABCNM.
Cho (H) là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a . Tính thể tích của (H)
Cho hình 20 mặt đều có các cạnh bằng 2 Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Mệnh đề nào sau đây đúng?
Hình lập phương có đường chéo của một mặt bên bằng 4cm. Tính thể tích của khối lập phương đó.
Cho khối tam giác có đường cao bằng 100cm và các cạnh đáy bằng 20cm, 21cm ,29cm . Tính thể tích của khối tam giác này.
Cho hình hộp ABCDA'B'C'D' có tất cả các cạnh đều bằng 2a đáy ABCD là hình vuông. Hình chiếu vuông góc của đỉnh lên mặt phẳng đáy trùng với tâm của đáy. Tính theo a thể tích V của khối hộp đã cho
Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
4
1
3
2
Mỗi cạnh của một khối đa diện là cạnh chung của bao nhiêu mặt của khối đa diện?
Ba mặt.
năm mặt.
Hai mặt.
Bốn mặt.
Trong các vật thể sau đây, vật thể nào là hình đa diện?

Cho hình chóp SABCDcó đáy ABCDlà hình thang vuông tại Góc giữa hai mặt phẳng ( SBC)và ( ABCD)là 60Gọi Ilà trung điểm của AD biết hai mặt phẳng ( SBI), ( CBI) cùng vuông góc với mặt phẳng ( ABCD)Tính thể tích khối chóp SABCD
Cho tứ diện ABCD có Khi thể tích khối tứ diện ABCD lớn nhất thì khoảng cách giữa hai đường thẳng AD và BC bằng
Cho hình chóp SABCD có đáy là hình thoi tâm O, , BD= 2a. Hai mặt phẳng (SAC) và ( SBD) cùng vuông góc với mặt đáy ( ABCD) . Biết khoảng cách từ tâm O đến ( SAB) bằng . Tính thể tích của khối chóp theo a.
Cho hình lập phương cạnh a Gọi M, N lần lượt là trung điểm của A'B' và BC Mặt phẳng chia khối lập phương đã cho thành hai khối đa diện. Gọi là khối đa diện chứa đỉnh A, là khối đa diện còn lại. Tính tỉ số
Cho hình chóp SABCD có đáy ABC là tam giác đều và có SA=SB=SC=1. Tính thể tích lớn nhất của khối chóp đã cho.