Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án- Đề 14
50 câu hỏi
Cho hàm số có bảng biến thiên dưới đây:
Khẳng định nào sau là đúng?
Hàm số đồng biến trên .
Hàm số đồng biến trên khoảng .
Hàm số đồng biến trên khoảng
Hàm số đồng biến trên khoảng .
Cho hàm số y=f(x) có đồ thị như hình vẽ dưới đây:
Khẳng định nào sau là đúng?
Hàm số nghịch biến trên khoảng .
Hàm số đồng biến trên khoảng .
Hàm số nghịch biến trên khoảng .
Hàm số đồng biến trên khoảng .
Cho hàm số y=f(x) có bảng biến thiên như sau:
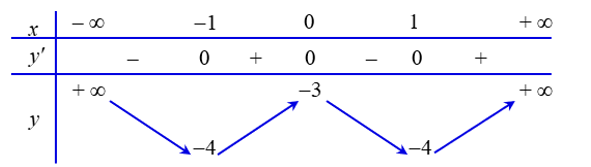
Khẳng định nào sau đây đúng
Hàm số đạt cực tiểu tại .
Điểm cực đại của đồ thị hàm số là x=0 .
Giá trị cực tiểu của hàm số bằng 1.
Điểm cực đại của đồ thị hàm số là .
Cho hàm số y=f(x), bảng xét dấu của f'(x) như sau
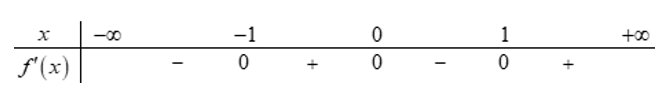
Số điểm cực tiểu của hàm số đã cho là
0
2
1
3
Giá trị nhỏ nhất của hàm số trên đoạn là
-1
2
3
1
Cho hàm số y=f(x) có bảng biến thiên ở hình vẽ bên dưới
Giá trị lớn nhất của hàm số y=f(x) trên khoảng là
2
0
1
4
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ:
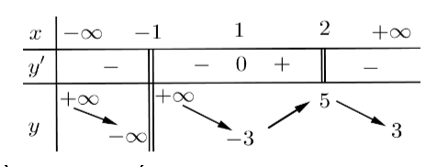
Số tiệm cận của đồ thị hàm số y=f(x) là
1
3
0
2
Cho hàm số y=f(x) có đồ thị là đường cong ( C) và các giới hạn
. Hỏi mệnh đề nào sau đây là đúng?
Đường thẳng x=2là tiệm cận đứng của ( C).
Đường thẳng y=2là tiệm cận ngang của ( C).
Đường thẳng y=1là tiệm cận ngang của ( C).
Đường thẳng x=2 là tiệm cận ngang của ( C).
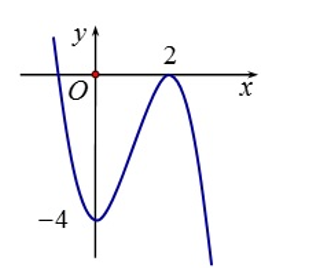
Đồ thị ở hình vẽ bên dưới là của hàm số nào trong các phương án cho dưới đây?
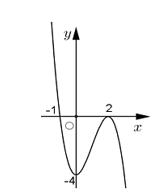
Đồ thị ở hình vẽ bên dưới là của hàm số nào trong các phương án cho dưới đây?
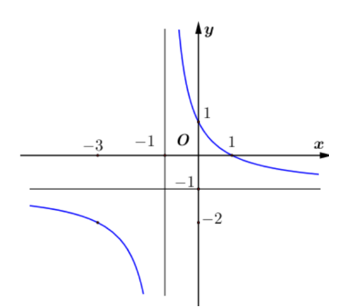
Số giao điểm của đồ thị hàm số với trục hoành là
1
0
2
3
Cho một hình đa diện. Khẳng định nào sau đây sai?
Mỗi cạnh là cạnh chung của ít nhất ba mặt.
Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
Mỗi mặt có ít nhất ba cạnh.
Trong các khối đa diện đều, khối đa diện lồi nào loại {5,3} ?
Khối 12mặt đều.
Khối lập phương.
Khối 20mặt đều.
Tứ diện đều.
Thể tích V của khối chóp đều có diện tích đáy bằng B và chiều cao bằng h là
Thể tích Vcủa khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h được tính theo công thức nào sau đây?
Cho hàm số có bảng biến thiên như hình vẽ . Giá trị nhỏ nhất của hàm số trên đoạn là
![Cho hàm số y=f(x) có bảng biến thiên như hình vẽ . Giá trị nhỏ nhất của hàm số f(x) trên đoạn [0,4] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/02/blobid2-1676705593.png)
-4
-1
-3
Cho hàm số có BBT như hình vẽ.
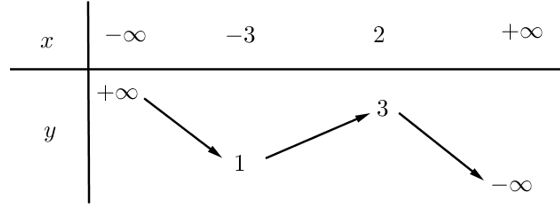
Hàm số f(x) đồng biến trên khoảng nào sau đây
Cho f(x) có bảng biến thiên như hình vẽ , hỏi tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y=f(x) là bao nhiêu ?
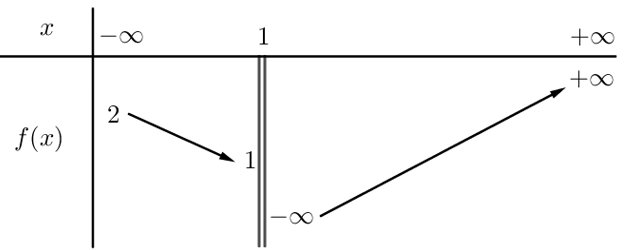
1
0
2
3
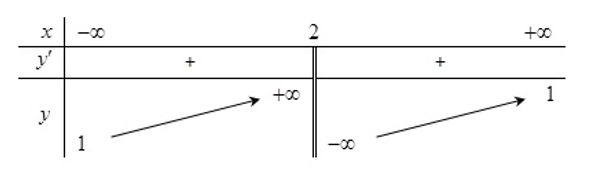
Cho hàm số . Kết luận nào sau đây về số tiệm cận của đồ thị hàm số là đúng?
Đồ thị có một tiệm cận ngang và tiệm cận đứng x=2
Đồ thị có một tiệm cận ngang và không có tiệm cận đứng.
Đồ thị có một tiệm cận ngang và hai tiệm cận đứng x=2, x=-1.
Đồ thị có hai tiệm cận ngang và tiệm cận đứng x=-1.
Tính thể tích V của khối lập phương ABCDA'B'C''D biết .
Cho hình hộp chữ nhật ABCDA'B'C'D' có . Tính theo a thể tích khối hộp đã cho.
Cho hàm số y=f(x) xác định trên R và có bảng biến thiên như hình vẽ. Kết luận nào sau đây là đúng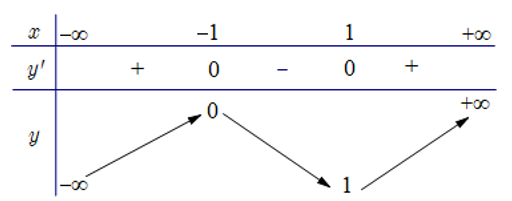
Hàm số đồng biến trên mỗi khoảng .
Hàm số đồng biến trên mỗi khoảng
Hàm số nghịch biến trên khoảng .
Hàm số đồng biến trên mỗi khoảng và nghịch biến trên khoảng .
Cho hàm số y=f(x) xác định trên và có đồ thị của hàm số f'(x) như hình vẽ. Mệnh đề nào sau đây đúng?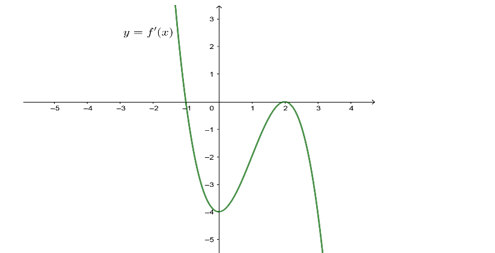
Hàm số đồng biến trên khoảng .
Hàm số đồng biến trên khoảng .
Hàm số đồng biến trên khoảng (0,2).
Hàm số nghịch biến trên khoảng và
Cho hàm số y=f(x) xác định trên R và có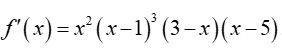 Số điểm cực tiểu của đồ thị hàm số là
Số điểm cực tiểu của đồ thị hàm số là
1
2
3
4
Cho hàm số y=f(x) có đạo hàm trên R và đồ thị của hàm số y=f'(x) như hình dưới đây
Số điểm cực đại của hàm số y=f(x) là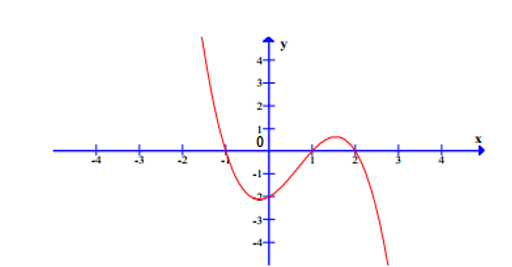
0
1
2
3
Giá trị lớn nhất của hàm số trên đoạn bằng:
0
4
8
2
Tìm tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số: .
3
4
2
1
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ. Bảng biến thiên đó là của hàm số nào?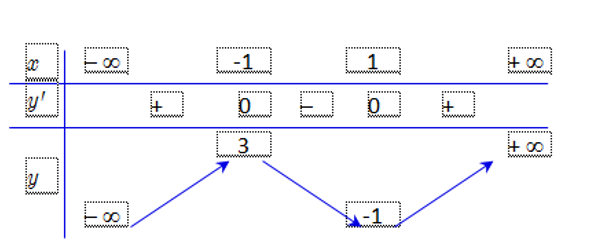
Số giao điểm của hai đồ thị hàm số và bằng
0
4
1
2
Cho hàm số có đồ thị (C) như hình vẽ dưới đây. Tìm tất cả các giá trị thực của tham số m để phương trình có ba nghiệm phân biệt.
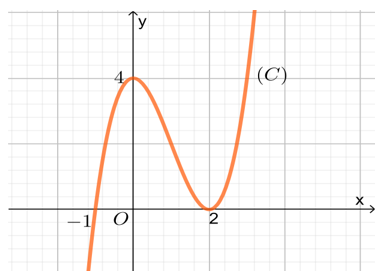
m>0
Cho , trong đó và phân số tối giản. Hãy tính giá trị biểu thức .
21
19
26
20
Mỗi hình sau gồm một số hữu hạn đa giác phẳng, tìm hình không là hình đa diện.
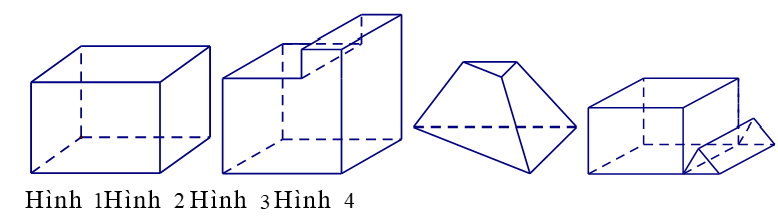
Hình 2.
Hình3
Hình 1.
Hình 3.
Tính tổng diện tích tất cả các mặt của khối đa diện đều loại có các cạnh bằng 1.
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B biết AB=a, AC=2a , và . Thể tích khối chóp SABC là:
Tính thể tích V của khối lăng trụ đều ABCA'B'C' biết AB=a và AB'=2a
Cho hình chóp SABC có và ; SB=3; SC=7. Tính thể tích V của khối chóp.
Cho hàm số (m là tham số thực). Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn để hàm số đồng biến trên khoảng
2018
2017
4036
4034
Tập hợp các giá trị của tham số m để hàm số đạt cực trị tại các điểm và thỏa mãn là
Cho hàm số có đồ thị (C). Khẳng định nào sau đây là đúng?
Đồ thị không có tiệm cận đứng và hai tiệm cận ngang.
Đồ thị không có tiệm cận đứng và có một tiệm cận ngang.
Đồ thị có một tiệm cận đứng và hai tiệm cận ngang.
Đồ thị có một tiệm cận đứng và một tiệm cận ngang
Cho hàm số có đồ thị như hình vẽ
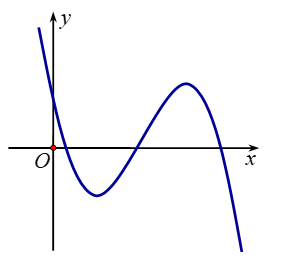
Mệnh đề nào sau đây đúng?
Cho hàm số có bảng biến thiên như hình vẽ:
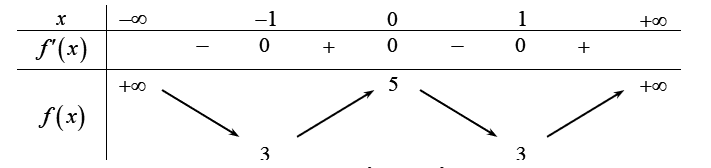
Tìm tất cả các giá trị thực của tham số m để phương trình có bốn nghiệm phân biệt.
Cho khối chóp SABCD có đáy ABCD là hình vuông cạnh , SA vuông góc với đáy và khoảng cách từ A đến mặt phẳng ( SBC) bằng . Thể tích V của khối chóp đã cho là
Cho hình lăng trụ tam giác đều ABCA'B'C' có góc giữa hai mặt phẳng (A'BC) và ( ABC) bằng , cạnh AB=a. Tính thể tích V của khối lăng trụ
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B. Biết SA vuông góc với mặt phẳng (ABC), . Một mặt phẳng qua A vuông góc SC tại H và SB cắt tại K. Tính thể tích khối chóp SAHK theo.
Cho hàm số . Đồ thị như hình bên dưới và .
![Cho hàm số y=f(x) . Đồ thị y= f'(x) như hình bên dưới và f(2)=f(-2)=0. Hàm số g(x)=[f(3-x)]^2 nghịch biến trong khoảng nào trong các khoảng sau? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/02/blobid1-1676725575.png)
Hàm số nghịch biến trong khoảng nào trong các khoảng sau?
Cho hàm số có đồ thị như hình bên dưới
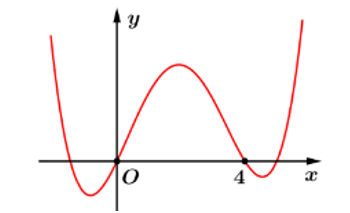
Số điểm cực trị của hàm số là
6
5
4
3
Ông A dự định sử dụng hết kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Cho hàm số liên tục trên R có đồ thị như hình vẽ bên dưới.
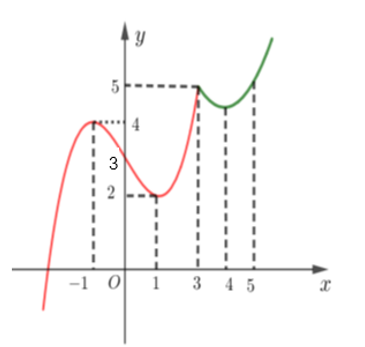
Tìm m để phương trình có đúng 6 nghiệm thực phân biệt thuộc ?
và
và
Cho hàm số có đạo hàm trên R và có đồ thị là đường cong trong hình
vẽ dưới. Đặt . Tìm số nghiệm của phương trình
![Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là đường cong trong hình vẽ dưới. Đặt g(x)= f[f(x)] . Tìm số nghiệm của phương trình g'(x)=0 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/02/blobid9-1676727290.png)
2
8
4
6
Cho hình chóp SABCD có đáy là hình bình hành và có thể tích V . Trên cạnh SA , SB lần lượt lấy các điểm M,N sao cho , . Mặt phẳng di động luôn đi qua M và N cắt các cạnh SC và SD lần lượt tại P và Q . Khi đó thể tích khối chóp đạt giá trị lớn nhất theo V bằng