Bộ 12 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 01
21 câu hỏi
Chọn khẳng định sai:
Với điều kiện các tỉ số đều có nghĩa thì
\[\frac{x}{a} = \frac{y}{b} = \frac{z}{c} = \frac{{x + y + z}}{{a + b + c}}\];
\[\frac{x}{a} = \frac{y}{b} = \frac{z}{c} = \frac{{x - y - z}}{{a - b - c}}\];
\[\frac{x}{a} = \frac{y}{b} = \frac{z}{c} = \frac{{x - y + z}}{{a - b + c}}\];
\[\frac{x}{a} = \frac{y}{b} = \frac{z}{c} = \frac{{x + y - z}}{{a - b + c}}\].
Cho biết y tỉ lệ thuận với x theo tỉ số k (k ≠ 0) và x tỉ lệ thuận với z theo tỉ số h (h ≠ 0). Chọn khẳng định đúng trong các khẳng định sau.
y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ h.k;
y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ \(\frac{k}{h}\);
y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ kh;
y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ hk.
Biểu thức nào sau đây là biểu thức số?
2.(32 + 4);
xy;
5x;
z2 + t3.
Mệnh đề “Tổng các lập phương của hai số a và b” được biểu thị bởi
a3 + b3;
(a + b)3;
a2 + b2;
(a + b)2.
Dựa vào hình vẽ và chọn đáp án đúng.
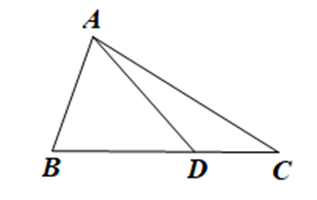
AB + BD > AC;
AD + DC > AC;
AB + AD > BC;
AB + BC < AC.
Cho DAMN = DDEK. Đâu là cách kí hiệu bằng nhau khác của hai tam giác trên?
DANM = DDEK;
DANM = DDKE;
DMAN = DEKD;
DMAN = DDKE.
Cho tam giác ABC. Ba đường trung tuyến của tam giác ABC cùng đi qua một điểm M. Khẳng định nào sau đây là đúng?
M cách đều ba đỉnh của tam giác ABC;
M cách đều ba cạnh của tam giác ABC;
M là trọng tâm tam giác ABC;
M là trực tâm tam giác ABC.
Một phép thử nghiệm có n kết quả và tất cả các kết quả đều có khả năng như nhau. Khi đó xác suất xảy ra của mỗi kết quả đều bằng:
n;
\[\frac{1}{n}\];
\(\frac{1}{{2n}}\);
\(\frac{1}{{n + 1}}\).
Tìm x, biết:
\[\frac{{x - 1}}{3} = \frac{1}{2}\];
Tìm x, biết:
5x(x – 3) = (x – 2)(5x – 1) – 5.
Cho hai đa thức A(x) = x – 2x2 + 3x5 + x4 + x + x2;
B(x) = –2x2 + x – 2 – x4 + 3x2 – 3x5.
Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.
Cho hai đa thức A(x) = x – 2x2 + 3x5 + x4 + x + x2;
B(x) = –2x2 + x – 2 – x4 + 3x2 – 3x5.
Tìm đa thức M(x) sao cho B(x) = A(x) + M(x). Tìm bậc và hệ số cao nhất của đa thức M(x).
Cho hai đa thức A(x) = x – 2x2 + 3x5 + x4 + x + x2;
B(x) = –2x2 + x – 2 – x4 + 3x2 – 3x5.
Tìm nghiệm của đa thức N(x) biết A(x) = N(x) – B(x).
Ba phân xưởng in có tổng cộng có 47 máy in (có cùng công suất in) và mỗi phân xưởng được giao in một số trang in bằng nhau. Phân xưởng thứ nhất hoàn thành công việc trong 3 ngày, phân xưởng thứ hai trong 4 ngày và phân cưởng thứ ba trong 5 ngày. Hỏi mỗi phân xưởng có bao nhiêu máy in?
Một chiếc hộp kín có chứa 5 quả bóng có kích thước và khối lượng như nhau, và được ghi lần lượt các số 5; 10; 15; 20; 25. Lấy ra ngẫu nhiên 1 quả bóng từ hộp. Xét các biến cố sau:
A: “Quả bóng lấy ra ghi số nguyên tố”;
B: “Quả bóng lấy ra ghi số chia hết cho 5”;
C: “Quả bóng lấy ra ghi số chia hết cho 6”.
D: “Quả bóng lấy ra ghi số tròn chục”.
Trong các biến cố trên, chỉ ra biến cố nào là chắc chắn, không thể.
Một chiếc hộp kín có chứa 5 quả bóng có kích thước và khối lượng như nhau, và được ghi lần lượt các số 5; 10; 15; 20; 25. Lấy ra ngẫu nhiên 1 quả bóng từ hộp. Xét các biến cố sau:
A: “Quả bóng lấy ra ghi số nguyên tố”;
B: “Quả bóng lấy ra ghi số chia hết cho 5”;
C: “Quả bóng lấy ra ghi số chia hết cho 6”.
D: “Quả bóng lấy ra ghi số tròn chục”.
Tính xác suất của các biến cố A và D.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
So sánh các góc của tam giác ABC.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
Chứng minh DABM = DDBM. Từ đó suy ra MA = MD.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
Tam giác MNC là tam giác gì? Tại sao?
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
Gọi I là trung điểm của CN. Chứng minh ba điểm B, M, I thẳng hàng.
Tìm giá trị nguyên dương của x để đa thức x3 – 3x2 – 3x – 1 chia hết cho đa thức x2 + x + 1.








