12 câu hỏi
Điểm \(M\left( {{x_0};{y_0}} \right)\) thì \({y_0}\) được gọi là
Hoành độ.
Tung độ.
Gốc tọa độ.
Giao điểm.
Điểm trong mặt phẳng tọa độ có hoành độ âm và tung độ dương sẽ nằm ở góc phần tư thứ mấy?
\(I.\)
\(II.\)
\(III.\)
\(IV.\)
Đồ thị hàm số \(y = ax + b\) với \(a \ne 0\) là gì?
Một đường thẳng.
Một đoạn thẳng.
Một đường cong.
Một đường tròn.
Hệ số \(b\) của đường thẳng \(y = 2\left( {3x - 5} \right) - 7\) là
\( - 7.\)
\( - 5.\)
\(6.\)
\( - 17.\)
Cho các phương trình dưới đây, phương trình bậc nhất một ẩn là
\(\frac{{2x}}{3} + 2 = 0\).
\(\frac{3}{x} + \frac{x}{2} = 0\).
\({x^2} + 2x + 1 = 0\).
\(2x - y = 0\).
Giá trị \(x = - 2\) là nghiệm của phương trình nào trong các phương trình sau?
\(x + 5 = 0\).
\(3x + 1 = 0\).
\(x - 2 = 0\).
\(2x + 4 = 0\).
Nếu một vòi nước chảy đầy bể trong \(5\) giờ thì trong một giờ vòi nước đó chảy được bao nhiêu phần của bể?
\(1.\)
\(\frac{1}{4}.\)
\(\frac{1}{5}.\)
\(\frac{1}{2}.\)
Một ô tô đi từ \(A\) đến \(B\) từ \(6\) giờ sáng, lúc \(7\) giờ sáng cùng ngày, một xe khách cũng đi từ \(A\) và tới \(B\) cùng lúc với ô tô. Vậy nếu gọi thời gian đi của xe khách là \(x\) (giờ) thì thời gian đi của ô tô là:
\(x + 1\) (giờ).
\(x - 1\) (giờ).
\(2\) (giờ).
\(x\) (giờ).
Cho \(\Delta ABC\) có \(DE\parallel BC\) như hình dưới đây.
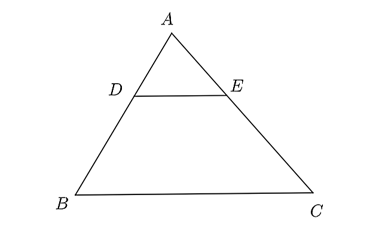
Theo định lí Thalès, ta có:
\(\frac{{AC}}{{CE}} = \frac{{AB}}{{AD}}.\)
\(\frac{{CE}}{{EA}} = \frac{{BD}}{{DA}}.\)
\(\frac{{AC}}{{CE}} = \frac{{BC}}{{CD}}.\)
\(\frac{{AC}}{{BC}} = \frac{{CD}}{{CE}}.\)
Cho hình vẽ dưới đây, biết \(IK\parallel GH\), \(\frac{{FI}}{{FG}} = \frac{1}{3}\).
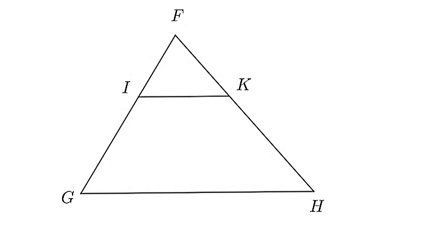
Khi đó, tỉ số nào sau đây có giá trị bằng \(\frac{1}{3}\)?
\(\frac{{FI}}{{IG}}.\)
\(\frac{{FK}}{{FH}}.\)
\(\frac{{FK}}{{KH}}.\)
\(\frac{{GH}}{{IK}}.\)
Cho hình vẽ dưới đây.
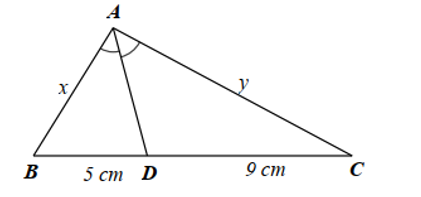
Tỉ số \(\frac{y}{x}\) là
\(\frac{5}{9}.\)
\(\frac{9}{5}.\)
\(\frac{9}{{14}}.\)
\(\frac{{14}}{9}.\)
Cho \(\Delta ABC\) có \(K,F\) lần lượt là trung điểm của \(AB,BC\). Khẳng định nào dưới đây là đúng?
\(KF = 2AC.\)
\(AC = 2KF.\)
\(AC = \frac{1}{2}KF.\)
\(KF = \frac{1}{3}AC.\)
