Bài tập Nhị thức Newton cơ bản, nâng cao có lời giải (P1)

Giả sử a, b là các số thực sao cho $x^3+y^3=a.{10}^{3z}+b.{10}^{2z}$ đúng với mọi các số thực dương x, y, z thỏa mãn 

$\log \left(x+y\right)=z$ và $\log \left(x^2+y^2\right)=z+1$. Giá trị của a+b bằng

Cho $\overline{)k,n}\left(k<n\right)$ là các số nguyên dương. Mệnh đề nào sau đây sai?

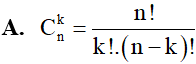
Cho biểu thức $P={\left(\frac{x+1}{\sqrt[3]{x^2}-\sqrt[3]{x+1}}-\frac{x-1}{x-\sqrt{x}}\right)}^{10}$ với x>0, x$\ne$1. Tìm số hạng không chứa x trong khai triển nhị thức Newton của P.

Tìm hệ số của $x^5$ trong khai triển nhị thức Newton ${\left(x\sqrt{x}+\frac{1}{\sqrt[3]{x}}\right)}^n$, biết tổng các hệ số của khai triển bằng 128

Tổng của n số hạng đầu tiên của một dãy số $\left(a_n\right), n\ge 1$ là $S_n=2n^2+3n$. Khi đó 

Cho dãy số $\left(U_n\right)$ xác định bởi $\left(U_1\right)=\frac{1}{3}$ và $U_{n+1}=\frac{n+1}{3n}{U}_n$. Tổng $S=U_1+\frac{U_2}{2}+\frac{U_3}{3}+...+\frac{U_{10}}{10}$bằng

Cho n là số nguyên dương thỏa mãn: $A_n^2=C_n^2+C_n^1+4n+6$. Hệ số của số hạng chứa $x^9$của khai triển biểu thức $P\left(x\right)={\left(x^2+\frac{3}{n}\right)}^n$ bằng:

Tính tổng $S=1+2.2+3.2^2+4.2^3+...+2018.2^{2017}$

Tìm hệ số của số hạng chứa $x^9$trong khai triển nhị thức Newton $\left(1+2x\right){\left(3+x\right)}^{11}$.

Tìm hệ số của $x^9$ trong khai triển biểu thức ${\left(2x^4-\frac{3}{x^3}\right)}^4$

Gọi S là tập hợp tất cả các số tự nhiên k sao cho $C_{14}^k, C_{14}^{k+1}, C_{14}^{k+2}$ theo thứ tự đó lập thành một cấp số cộng. Tính tích tất cả các phần tử của S.

Tìm hệ số của $x^4$ trong khai triển nhị thức Newton ${\left(2x+\frac{1}{\sqrt[5]{x}}\right)}^n$với x > 0, biết n là số tự nhiên lớn nhất thỏa mãn $A_n^5 \le 18A_{n-2}^4$

Trong khai triển biểu thức ${\left(x+y\right)}^{21}$ hệ số của số hạng chứa $x^{13}{y}^8$ là

Tìm số hạng không chứa x trong khai triển nhị thức Newton ${\left(x-\frac{2}{x^2}\right)}^{21}$, (x$\ne$0, $n\in N^{*}$)

Biết rằng hệ số của $x^4$ trong khai triển nhị thức Newton ${\left(2-x\right)}^n, \left(n\in N^{*}\right)$ bằng 60. Tìm n.

Tìm tất cả các số a trong khai triển của $\left(1+ax\right){\left(1+x\right)}^4$ có chứa số hạng $22x^3$

Tìm hệ số của $x^5$ trong khai triển $P\left(x\right)={\left(x+1\right)}^6+{\left(x+1\right)}^7+...+{\left(x+1\right)}^{12}$

Cho đa thức $$\begin{gathered} p\left(x\right)={\left(1+x\right)}^8+{\left(1+x\right)}^9 \\ +{\left(1+x\right)}^{10}+{\left(1+x\right)}^{11}{\left(1+x\right)}^{12} \end{gathered}$$. Khai triển và rút gọn ta được đa thức:  $$\begin{gathered} P\left(x\right)=a_0+a_{1}x+a_2{x}^2 \\ +...+a_{12}{x}^{12} \end{gathered}$$. Tìm hệ số $a_8$

Cho đa thức $$\begin{gathered} p\left(x\right)={\left(1+x\right)}^8+{\left(1+x\right)}^9 \\ +{\left(1+x\right)}^{10}+{\left(1+x\right)}^{11}{\left(1+x\right)}^{12} \end{gathered}$$. Khai triển và rút gọn ta được đa thức:  $$\begin{gathered} P\left(x\right)=a_0+a_{1}x+a_2{x}^2 \\ +...+a_{12}{x}^{12} \end{gathered}$$. Tìm tổng các hệ số $a_i,i=0,1,2,...,12$

Tìm hệ số h của số hạng chứa $x^5$ trong khai triển ${\left(x^2+\frac{2}{x}\right)}^7$?

Biết n là số nguyên dương thỏa mãn $A_n^3+2A_n^2=100$. Hệ số của $x^5$ trong khai triển ${\left(1-3x\right)}^{2n}$ bằng:

Cho tổng $S=C_{2017}^1+C_{2017}^2+...+C_{2017}^{2017}$. Giá trị tổng S bằng:

Tính tổng $S=C_{2018}^{1009}+C_{2018}^{1010}+C_{2018}^{1011}+...+C_{2018}^{2018}$ (trong tổng đó, các số hạng có dạng $C_{2018}^k$ với k nguyên dương nhận giá trị liên tục từ 1009 đến 2018).

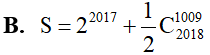
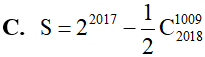
Hệ số của $x^9$ sau khi khai triển và rút gọn đa thức $$\begin{gathered} f\left(x\right)={(1+x)}^9+{(1+x)}^{10} \\ +...+{(1+x)}^{14} \end{gathered}$$ là:

Cho ${\left(x+\frac{1}{2}\right)}^{40}=\sum _{k=0}^{40}{a}_k{x}^k$, với $a_k\in \mathrm{ℝ}$. Khẳng định nào sau đây là đúng?

Tìm hệ số của $x^7$ trong khai triển $P\left(x\right)={\left(x+1\right)}^{20}$ 

Trong khai triển ${\left(\frac{1}{x^3}+x^5\right)}^{12}$ với x$\ne$0. Số hạng chứa $x^4$ là:

Với n là số nguyên dương thỏa mãn $A_n^k+2A_n^2=100$ ($A_n^k$ là số các chỉnh hợp chập k của tập hợp có n phần tử). Số hạng chứa $x^5$ trong khai triển của biểu thức ${\left(1+3x\right)}^{2n}$ là:

Trong khai triển ${\left(a-2b\right)}^8$, hệ số của số hạng chứa $a^4{b}^4$ là: