20 câu hỏi
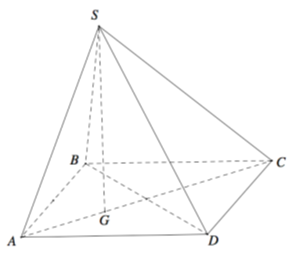
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 6a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trọng tâm G của tam giác ABD d(G,(SAD))=a (tham khảo hình vẽ bên). Tính khoảng cách giữa hai đường thẳng SD và BC.
2a
3a
4a
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và OA =OB =a, OC=2a. Thể tích khối cầu ngoại tiếp tứ diện OABC bằng
Cho khối hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, AB = AD= Hai mặt bên (ABB'A) (ADD'A') tạo với đáy các góc lần lượt là và . Tính thể tích V của khối hộp đã cho biết độ dài cạnh bên bằng 1.
V = 3
V =
V =
V =
Cho hình chóp S.ABC có AB=2a, BC = a, Biết mặt phẳng (SAC) vuông góc với mặt phẳng (ABC), d(C,SA)=2. Côsin góc giữa hai mặt phẳng (SAC) và (SAB) bằng
.
Cho khối chóp có đáy là tam giác đều. Nếu tăng độ dài của ba cạnh đáy lên m lần và giảm độ dài chiều cao m lần thì thể tích khối chóp khi đó sẽ thay đổi như thế nào so với ban đầu ?
tăng m lần
tăng lần
giảm lần
không thay đổi
Một khối lăng trụ tam giác có cạnh đáy lần lượt là 6cm , 8cm và 10cm , cạnh bên 14cm và góc giữa cạnh bên và mặt đáy bằng . Tính thể tích của khối đó.
112
168
Cho hình bát diện đều. Biết rằng các điểm là tâm các mặt của bát diện đều tạo thành một hình đa diện đều. Tên của hình đa diện đó là
tứ diện đều
lập phương
bát diện đều
mười hai mặt đều.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB =2a, BC =a. Các cạnh bên của hình chóp bằng nhau và bằng a . Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên BC. Khoảng cách giữa hai đường thẳng EF và SK là:
Cho khối lăng trụ đứng ABC.DEF có đáy là tam giác vuông tại A với BC =4a . Biết có chu vi bằnga. Thể tích khối lăng trụ ABC.DEF là
Cho hình chóp S.ABC . có đáy ABC là tam giác vuông tại B . Các mặt bên (SAC); (SAB) cùng vuông góc với đáy,, SC = 2. Gọi là góc hợp bởi hai mặt phẳng (ABC), (SBC) . Giá trị biểu thức
0
1
2
3
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc . Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và . Khoảng cách từ A đến mặt phẳng (SBC) là:
Cho hình lập phương ABCD.A' B'C' D' cạnh bằng a và K là một điểm nằm trên cạnh CC’ sao cho . Mặt phẳng qua A, K và song song với BD chia khối lập phương thành hai phần có thể tích . Tính tỉ số
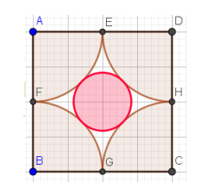
Hai người cùng chơi trò chơi phóng phi tiêu, mỗi người đứng cách một tấm bảng hình vuông ABCD có kích thước là 4x4 dm một khoảng cách nhất định. Mỗi người sẽ phóng một cây phi tiêu vào tấm bảng hình vuông ABCD (như hình vẽ). Nếu phi tiêu cắm vào hình tròn tô màu hồng thì người đó sẽ được 10 điểm. Xét phép thử là hai người lần lượt phóng 1 cây phi tiêu vào tấm bảng hình vuông ABCD (phép thử này đảm bảo khi phóng là trúng và dính vào tấm bảng hình vuông, không rơi ra ngoài). Tính xác suất để có đúng một trong hai người phóng phi tiêu được 10 điểm. ( kết quả cuối cùng làm tròn số đến 4 chữ số thập phân)
0,2331
0,2330
0,2333
0,2332
Mặt phẳng (AB'C') chia khối lăng trụ ABC.A'B'C' thành các khối đa diện nào?
Một khối chóp tam giác và một khối chóp ngũ giác.
Một khối chóp tam giác và một khối chóp tứ giác
Hai khối chóp tam giác
Hai khối chóp tứ giác
Hình đa diện nào sau đây không có tâm đối xứng?
Tứ diện đều.
Bát diện đều.
Lục diện đều.
Thập nhị diện đều.
Tìm tổng số đỉnh và cạnh của hình bát diện đều.
14.
20.
18.
26.
Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng 2a là:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA (ABC), SA= 3a, AB=a, BC=2a. Gọi E là trung điểm BC. Tính góc giữa đường thẳng SE và mặt phẳng (ABC)
.
.
.
.
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, AB = 6a, AC= 7a, AD = 8a . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là:
14.
28.
42.
7.
Cho tứ diện ABCD có BC = CD = BD = 2a, AC = AD =, AB = a. Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là:
.
.








