Quiz

Bài tập Hình học không gian ôn thi THPT Quốc gia có lời giải (P3)

VietJackToánLớp 112 lượt thi

Xem trước Bắt đầu ngay

20 câu hỏi

Hiển thị đáp án

1. Trắc nghiệm

• 1 điểm • Không giới hạn

Khối lăng trụ tam giác đều có tất cả các cạnh bằng 1 có thể tích bằng

$\frac{\sqrt{3}}{12}$

$\frac{\sqrt{3}}{4}$

$\frac{4 \sqrt{3}}{3}$

$\frac{4 \sqrt{3}}{9}$

Xem đáp án

2. Trắc nghiệm

• 1 điểm • Không giới hạn

Một khối nón và một khối trụ có chiều cao và bán kính đáy đều bằng 1. Tổng thể tích của khối nón và khối trụ đó bằng

$\frac{4 π}{3}$

$\frac{10 π}{3}$

$4 π$

$\frac{2 π}{3}$

Xem đáp án

3. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên).

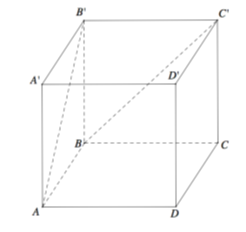
6 $0^{o}$

9 $0^{o}$

$45^{o}$

3 $0^{o}$

Xem đáp án

4. Trắc nghiệm

• 1 điểm • Không giới hạn

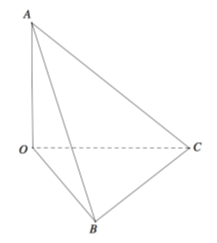
Tứ diện OABC có OA,OB,OC đôi một vuông góc và OA =1, OB=2, OC=3. Tang của góc giữa đường thẳng OA và mặt phẳng (ABC) bằng

$\frac{6}{7}$

$\frac{\sqrt{13}}{6}$

$\frac{6 \sqrt{13}}{13}$

$\frac{6 \sqrt{7}}{7}$

Xem đáp án

5. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình tứ diện đều ABCD có cạnh bằng a. Côsin của góc tạo bởi hai mặt có chung một cạnh của tứ diện đều bằng

$\frac{2}{3}$

$\frac{1}{3}$

$\frac{\sqrt{2}}{4}$

$\frac{\sqrt{2}}{8}$

Xem đáp án

6. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tam giác OAB vuông tại O, OA=OB= 4. Lấy một điểm M thuộc cạnh AB và gọi H là hình chiếu của M trên OA. Thể tích của khối tròn xoay được tạo thành khi quay tam giác OMH quanh OA có thể tích lớn nhất bằng

$\frac{256 π}{81}$

$\frac{81 π}{256}$

$\frac{128 π}{81}$

$\frac{8 π}{3}$

Xem đáp án

7. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối lăng trụ tam giác đều ABC.A′B′C′ có cạnh đáy bằng a, góc giữa đường thẳng B′C và mặt đáy bằng $30^{o}$ . Khoảng cách giữa hai đường thẳng A′C và B′C′ bằng

$\frac{a \sqrt{15}}{15}$

$\frac{a \sqrt{15}}{5}$

$\frac{a \sqrt{3}}{13}$

$\frac{a \sqrt{39}}{13}$

Xem đáp án

8. Trắc nghiệm

• 1 điểm • Không giới hạn

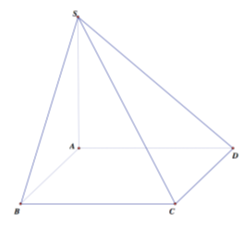
Cho khối chóp S.ABC có SA = SB = SC =a, $\hat{A S B} = 60^{o}$ , $\hat{B S C} = 90^{o}$ , $\hat{C S A} = 120^{o}$ Gọi M,N lần lượt là các điểm trên cạnh AB và SC sao cho $\frac{C N}{S C} = \frac{A M}{A B}$ Khi khoảng cách giữa M và N nhỏ nhất, tính thể tích V của khối chóp S.AMN.

$V = \frac{\sqrt{2} a^{3}}{72}$

$V = \frac{5 \sqrt{2} a^{3}}{72}$

$V = \frac{5 \sqrt{2} a^{3}}{432}$

$V = \frac{\sqrt{2} a^{3}}{432}$

Xem đáp án

9. Trắc nghiệm

• 1 điểm • Không giới hạn

Thể tích của khối tứ diện OABC có OA=OB= OC =a và OA,OB,OC đôi một tạo với nhau một góc $60^{o}$ bằng

$\frac{a^{3}}{6}$

$\frac{a^{3}}{3}$

$\frac{\sqrt{2} a^{3}}{12}$

$\frac{\sqrt{2} a^{3}}{4}$

Xem đáp án

10. Trắc nghiệm

• 1 điểm • Không giới hạn

Hình nón có góc ở đỉnh bằng $60^{0}$ và chiều cao bằng $\sqrt{3}$ . Độ dài đường sinh của hình nón là

$2 \sqrt{3}$

$2 \sqrt{2}$

Xem đáp án

11. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng

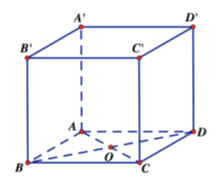
$a \sqrt{2}$

$a \sqrt{3}$

$\frac{a \sqrt{3}}{2}$

Xem đáp án

12. Trắc nghiệm

• 1 điểm • Không giới hạn

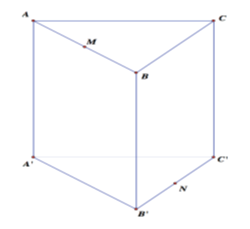
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M,N lần lượt là trung điểm các cạnh AB,B′C′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng MN và AC bằng

$\frac{1}{3}$

$\frac{\sqrt{5}}{3}$

$\frac{2}{3}$

$\frac{\sqrt{5}}{5}$

Xem đáp án

13. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA =a vuông góc với đáy. Côsin góc giữa đường thẳng SC và mặt phẳng (SBD) bằng

$\frac{1}{3}$

$\frac{2 \sqrt{2}}{3}$

$\frac{2}{3}$

$\frac{\sqrt{5}}{3}$

Xem đáp án

14. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tam giác ABC có diện tích bằng 30. Quay tam giác ABC quanh cạnh BC thu được vật thể tròn xoay có thể tích bằng 100π . Tính độ dài cạnh BC.

12.

18.

Xem đáp án

15. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình lăng trụ đứng ABC.A'B'C' có AA' = AB = AC =1 $\hat{B A C} = 120^{o}$ Gọi M là trung điểm cạnh CC′. Côsin góc giữa hai mặt phẳng (ABC) và (AB′M) bằng

$\frac{\sqrt{30}}{10}$

$\frac{\sqrt{70}}{10}$

$\frac{\sqrt{30}}{20}$

$\frac{\sqrt{370}}{20}$

Xem đáp án

16. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho khối tứ diện ABCD có AB = x, AC =AD = CB = DB = $2 \sqrt{3}$ khoảng cách giữa AB,CD bằng 1. Tìm x, để khối tứ diện ABCD có thể tích lớn nhất.

x = $\sqrt{11}$

x = $\sqrt{13}$

x = $\sqrt{26}$

x = $\sqrt{22}$

Xem đáp án

17. Trắc nghiệm

• 1 điểm • Không giới hạn

Khối chóp chóp tam giác S.ABC có thể tích V. Gọi M,N,P lần lượt là trung điểm các cạnh SA, SB, SC. Thể tích của khối đa diện ABCMNP bằng

$\frac{V}{8}$

$\frac{3 V}{4}$

$\frac{7 V}{8}$

$\frac{V}{4}$

Xem đáp án

18. Trắc nghiệm

• 1 điểm • Không giới hạn

Một hình trụ có bán kính đáy bằng 3 và chiều cao bằng 4. Diện tích xung quanh của hình trụ là

36 $π$

24 $π$

42 $π$

33 $π$

Xem đáp án

19. Trắc nghiệm

• 1 điểm • Không giới hạn

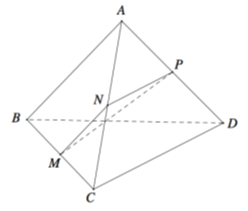
Cho tứ diện ABCD. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CA và AD (tham khảo hình vẽ bên). Biết $\hat{M N P} = 150^{o}$ Góc giữa hai đường thẳng AB và CD là