30 câu hỏi
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, A'A = A'B = A'C = BC = 2a (a>0).
a332
a33
a336
a333
Cho hình chóp tam giác đều S.ABC có SA = a, . Người ta muốn trang trí cho hình chóp bằng một dây đèn nháy chạy theo các điểm A, M, N rồi quay lại A (đúng một vòng) như hình bên dưới. Độ dài ngắn nhất của dây đèn nháy là:
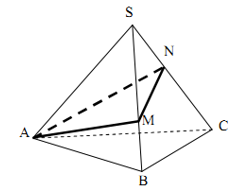
a22
a2
a3
a33
Khối đa diện mười hai mặt đều là khối đa diện đều loại:
{3;3}
{5;3}
{3;5}
{4;3}
Cho lăng trụ tam giác ABC.A’B’C’ có thể tích là V. Gọi M, N là trung điểm của AB và CC'. Thể tích khối tứ diện B’MCN tính theo V là:
Thể tích khối chóp tam giác đều có tất cả các cạnh bằng a
a324
a326
a3212
a3312
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với đáy, góc giữa SC và mặt đáy bằng , AB = a (a > 0). Thể tích của khối chóp S.ABC là:
a336
a36
a332
a333
Cho hình chóp S.ABCcó đáy ABC là tam giác đều cạnh AB = a (a > 0). Mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích khối chóp S.ABC là:
a3324
a338
a333
a336
Số cạnh của khối bát diện đều là
12
20
8
6
Cho hình lập phương ABCD.A’B’C’D có ẠC' = a (a > 0). Thế tích của khối lập phương đó là
a33
a339
a3
3a33
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, AD = DC = a, AB = 2a (a > 0). Hình chiếu của S lên mặt đáy trùng với trung điểm I của AD. Thể tích khối chóp S.IBC biết góc giữa SC và mặt đáy bằng
a3524
a31524
a358
a3158
Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy AB, AB = 2DC. Gọi M, N là trung điểm của SA và SD. Tính tỉ số thể tích của hai hình chóp
12
512
38
13
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh AB = a, AA'= 2a. Hình chiếu của A lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ là:
a3114
a31112
a3478
3a34
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh AB = a (a > 0). Góc giữa mặt bên và mặt đáy bằng . Tính thể tích khối chóp S.ABCD:
a332
a36
a333
a336
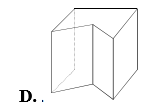
Trong các hình dưới đây, hình nào không phải hình đa diện?
Cho hình lăng trụ ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của AA’, BB’. Tính tỉ số
2
1,5
2,5
3
Cho hình chóp S.ABC có thể tích bằng 72. Gọi M là trung điểm của SA và N là điểm thuộc cạnh SC sao cho NC = 2NS. Tính thể tích V của khối đa diện MNABC
V = 48
V = 30
V = 24
V = 60
Tính tổng số đỉnh và số mặt của khối đa diện đều loại {5;3}
50
20
32
42
Tính thể tích V của khối chóp đều S.ABC có cạnh đáy bằng 2a và cạnh bên bằng a
V = a33
V = a353
V = a35
V = a333
Một hình đa diện, mệnh đề nào dưới đây đúng?
Hai mặt bất kì có ít nhất một điểm chung
Hai mặt bất kì có ít nhất một cạnh chung
Hai cạnh bất kì có ít nhất một điểm chung
Mỗi đỉnh là đỉnh chung của ít nhất ba mặt
Gia đình Toán xây một bể nước dạng hình hộp chữ nhật có nắp dung tích 2017 lít, Đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng được làm bằng bê tông có giá 350.000đồng/ thân bể được xây bằng gạch có giá 200.000 đồng và nắp bể được làm bằng tôn có giá 250.000 đồng/. Hỏi chi phí thấp nhất gia đình Toán cần bỏ ra để xây bể nước là bao nhiêu?
2.280.700 đồng
2.150.300 đồng
2.510.300 đồng
2,820.700 đồng
Hình hộp chữ nhật chỉ có hai đáy là hai hình vuông có tất cả bao nhiêu mặt phẳng đối xứng?
4
3
9
5
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, Biết AC = a và AB = a. Tính thể tích V của khối lăng trụ ABC.A’B’C’
V = 6
V =
V = 3
V = 9
Hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 1 và AD = . Cạnh bên SA vuông góc với mặt phẳng đáy và SC tạo với mặt phẳng (ABCD) một góc . Tính thể tích V của khối chóp S,ABCD
V = 3
V = 2
V = 6
V = 1
Tính thể tích V của hình lập phương có độ dài đường chéo bằng 6
V = 24
V = 8
V = 4
V = 12
Thị xã Từ Sơn xây dựng một ngọn tháp đèn lộng lẫy hình chóp tứ giác đều S.ABCD có cạnh bên SA = 12m và . Người ta cần mặc một đường dây điện từ điểm A đến trung điểm K của SA gồm 4 đoạn thẳng AE, EF, FH, HK như hình vẽ. Để tiết kiệm chi phí ngừơi ta cần thiết kế được chiều dài con đường từ A đến K là ngắn nhất. Tính tỉ số K =
k = 34
k = 12
k = 13
k = 23
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với AB = a và . Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC). Tính khoảng cách d từ điểm A đến mặt phẳng (SBC) biết khối chóp S.ABC có thể tích bằng
d = a25
d = a3
d = a55
d = a36
Cho hình chóp S.ABC có và SA = SB = SC = a. Tính khoảng cách d từ điểm A đến mặt phẳng (SBC)
d = 2a6
d = a63
d = 2a63
d = a6
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AA' = 2a, AD = 4a. Gọi M là trung điểm của cạnh AD. Tính khoảng cách d từ giữa hai đường thẳng A’B’ và C’M
d = 2a2
d = a2
d = 2a
d = 3a
Tính thể tích của một khối lăng trụ biết khối lăng trụ đó có đường cao bằng 3a, diện tích mặt đáy bằng 4
12
4
12
4
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a, SA vuông góc với đáy và SA = a Tính thể tích khối chóp S.ABCD
2a33
4a33
4a333
2a333








