Quiz

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P8)

Admin30 câu hỏiToánLớp 11

Bắt đầu ngay

30 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

1 điểm • Không giới hạn

Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?

A. Hai đường thẳng cắt nhau.

B. Ba điểm phân biệt

C. Bốn điểm phân biệt

D. Một điểm và một đường thẳng.

Xem giải thích câu trả lời

2. Nhiều lựa chọn

1 điểm • Không giới hạn

Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 147m, cạnh đáy dài 230m. Thế tích của nó là:

A. 7776300 $m^{3}$

B. 3888150 $m^{3}$

C. 2592100 $m^{3}$

D. 2592100 $m^{2}$

Xem giải thích câu trả lời

3. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình tứ diện ABCD có trọng tâm G . Mệnh đề nào sau đây là sai?

$A . \overset{⇀}{G A} + \overset{⇀}{G B} + \overset{⇀}{G C} + \overset{⇀}{G D} = 0$

$B . \overset{⇀}{O G} = \frac{1}{4} (\overset{⇀}{O A} + \overset{⇀}{O B} + \overset{⇀}{O C} + \overset{⇀}{O D})$

$C . \overset{⇀}{A G} = \frac{1}{4} (\overset{⇀}{A B} + \overset{⇀}{A C} + \overset{⇀}{A D})$

$D . \overset{⇀}{A G} = \frac{2}{3} (\overset{⇀}{A B} + \overset{⇀}{A C} + \overset{⇀}{A D})$

Xem giải thích câu trả lời

4. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình đa diện đều loại {4;3} cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?

$A . S = 6 a^{2}$

$B . S = 4 a^{2}$

$C . S = 8 a^{2}$

$D . S = 10 a^{2}$

Xem giải thích câu trả lời

5. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho khối chóp S.ABCD có ABCD là hình vuông có cạnh đáy bằng 3a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp biết tam giác SAB vuông.

$A . 9 a^{3}$

$B . \frac{9 a^{3} \sqrt{3}}{2}$

$C . \frac{9 a^{3}}{2}$

$D . 9 a^{3} \sqrt{3}$

Xem giải thích câu trả lời

6. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là một hình vuông cạnh a. Các mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC tạo với mặt phẳng đáy một góc $60^{0}$ . Thể tích của khối chóp đã cho bằng:

$A . \frac{a^{3} \sqrt{6}}{5}$

$B . \frac{a^{3} \sqrt{6}}{3}$

$C . \frac{a^{3} \sqrt{6}}{4}$

$D . \frac{a^{3} \sqrt{6}}{9}$

Xem giải thích câu trả lời

7. Nhiều lựa chọn

1 điểm • Không giới hạn

Từ một mảnh giấy hình vuông cạnh a , người ta gấp thành hình lăng trụ theo hai cách sau:

Cách 1. Gấp thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều có thể tích là (Hình 1).

Cách 2. Gấp thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều có thể tích là (Hình 2).

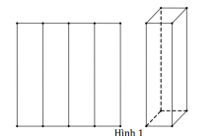
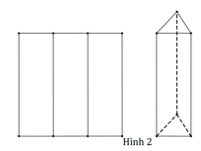
Tính tỉ số k = $\frac{V_{1}}{V_{2}}$

A. k = $\frac{3 \sqrt{3}}{8}$

B. k = $\frac{3 \sqrt{3}}{2}$

C. k = $\frac{4 \sqrt{3}}{9}$

D. k = $\frac{3 \sqrt{3}}{4}$

Xem giải thích câu trả lời

8. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a . Gọi M , N lần lượt là trung điểm các cạnh AC , BC ; P là trọng tâm tam giác BCD . Mặt phẳng (MNP) cắt tứ diện theo một thiết diện có diện tích là:

$A . \frac{a^{2} \sqrt{11}}{2}$

$B . \frac{a^{2} \sqrt{2}}{4}$

$C . \frac{a^{2} \sqrt{11}}{4}$

$D . \frac{a^{2} \sqrt{3}}{4}$

Xem giải thích câu trả lời

9. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp tam giác đều S.ABC cạnh đáy bằng 2a và chiều cao bằng a $\sqrt{3}$ . Tính khoảng cách từ tâm O của đáy ABC đến một mặt bên:

$A . a \sqrt{\frac{3}{10}}$

$B . \frac{2 a \sqrt{3}}{3}$

$C . a \sqrt{\frac{2}{5}}$

$D . \frac{a \sqrt{5}}{2}$

Xem giải thích câu trả lời

10. Nhiều lựa chọn

1 điểm • Không giới hạn

Một người xây nhà xưởng hình hộp chữ nhật có diện tích mặt sàn là 1152 $m^{2}$ và chiều cao cố định. Người đó xây các bức tường xung quanh và bên trong để ngăn nhà xưởng thành ba phòng hình chữ nhật có kích thước như nhau (không kể trần nhà). Vậy cần phải xây các phòng theo kích thước nào để tiết kiệm chi phí nhất (bỏ qua độ dày các bức tường).

A. 16m x 24m

B. 8m x 48m

C. 12m x 32m

D. 24m x 32m

Xem giải thích câu trả lời

11. Nhiều lựa chọn

1 điểm • Không giới hạn

Một người cần làm một hình lăng trụ tam giác đều từ tấm nhựa phẳng để có thể tích là $6 \sqrt{3} c m^{3}$ . Để ít hao tốn vật liệu nhất thì cần tính độ dài các cạnh của khối lăng trụ tam giác đều này bằng bao nhiêu?

A. Cạnh đáy bằng 4 $\sqrt{3}$ và cạnh bên bằng $\frac{1}{2}$ cm

B. Cạnh đáy bằng $2 \sqrt{6}$ và cạnh bên bằng 1 cm

C. Cạnh đáy bằng $2 \sqrt{2}$ và cạnh bên bằng 3 cm

D. Cạnh đáy bằng 2 $\sqrt{3}$ và cạnh bên bằng 2cm

Xem giải thích câu trả lời

12. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp tam giác S.ABC có thể tích bằng 8. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA. Tính thể tích khối chóp S.MNP

A. 3

B. 6

C. 2

D. 4

Xem giải thích câu trả lời

13. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với (ABCD). Gọi là góc giữa BD và (SAD). Tính sin $α$

A. sin $α$ = $\frac{\sqrt{6}}{4}$

B. sin $α$ = $\frac{1}{2}$

C. sin $α$ = $\frac{\sqrt{3}}{2}$

D. sin $α$ = $\frac{\sqrt{10}}{4}$

Xem giải thích câu trả lời

14. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Tính khoảng cách giữa hai mặt phẳng (A’B’D’) và (BC’D)

$A . \frac{\sqrt{3}}{3}$

$B . \sqrt{3}$

$C . \frac{\sqrt{3}}{2}$

$D . \frac{2}{\sqrt{3}}$

Xem giải thích câu trả lời

15. Nhiều lựa chọn

1 điểm • Không giới hạn

Tính thể tích V của khối lập phương ABCD.A’B’C’D’ biết AC' = a $\sqrt{3}$

$A . V = a^{3}$

$B . V = \frac{a^{3}}{4}$

$C . V = \frac{3 \sqrt{6} a^{3}}{4}$

$D . V = 3 \sqrt{3} a^{3}$

Xem giải thích câu trả lời

16. Nhiều lựa chọn

1 điểm • Không giới hạn

Hỏi khối đa diện đều loại {4;3} có bao nhiêu mặt?

A. 4

B. 7

C. 8

D. 6

Xem giải thích câu trả lời

17. Nhiều lựa chọn

1 điểm • Không giới hạn

Lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng 4 và diện tích tam giác A’BC bằng 8. Tính thể tích khối lăng trụ đó

$A . 8 \sqrt{3}$

$B . 6 \sqrt{3}$

$C . 4 \sqrt{3}$

$D . 2 \sqrt{3}$

Xem giải thích câu trả lời

18. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a, hình chiếu của A’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết góc giữa cạnh bên và mặt phẳng đáy bằng $60^{0}$ . Tính thể tích khối lăng trụ ABC.A’B’C’

$A . \frac{a^{3} \sqrt{3}}{4}$

$B . 4 a^{3} \sqrt{3}$

$C . 2 a^{3} \sqrt{3}$

$D . \frac{a^{3} \sqrt{3}}{2}$

Xem giải thích câu trả lời

19. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho khối hộp ABCD.A’B’C’D’. Gọi M, N, P lần lượt là trung điểm của AB, AD và AA’. Tính tỉ số thể tích k của khối chóp A.MNP và khối hộp đã cho

$A . k = \frac{1}{12}$

$B . k = \frac{1}{48}$

$C . k = \frac{1}{8}$

$D . k = \frac{1}{24}$

Xem giải thích câu trả lời

20. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, AD = 2a. Cạnh bên SA vuông góc với đáy (ABCD), Tính tan của góc giữa hai ămtj phẳng (SBD) và (ABCD)

$A . \frac{1}{\sqrt{5}}$

$B . \frac{2}{\sqrt{5}}$

$C . \sqrt{5}$

$D . \frac{\sqrt{5}}{2}$

Xem giải thích câu trả lời

21. Nhiều lựa chọn

1 điểm • Không giới hạn

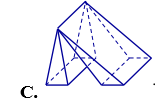
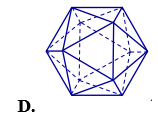
Vật thể nào trong các vật thể sau không phải khối đa diện?

Xem giải thích câu trả lời

22. Nhiều lựa chọn

1 điểm • Không giới hạn

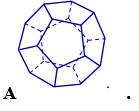
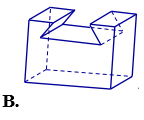
Cho hình lập phương ABCD.A’B’C’D’. Khẳng định nào sau đây là khẳng định sai?

A. Góc giữa hai đường thẳng B’D’ và AA’ bằng $60^{0}$

B. Góc giữa hai đường thẳng AC và B’D’ bằng $90^{0}$

C. Góc giữa hai đường thẳng AD và B’C bằng $45^{0}$

D. Góc giữa hai đường thẳng BD và A’C’ bằng $90^{0}$

Xem giải thích câu trả lời

23. Nhiều lựa chọn

1 điểm • Không giới hạn

Tính độ dài cạnh bên l của khối lăng trụ đứng có thể tích V và diện tích đáy bằng S

$A . l = \frac{\sqrt{V}}{S}$

$B . l = \frac{V}{2 S}$

$C . l = \frac{V}{S}$

$D . l = \frac{3 V}{S}$

Xem giải thích câu trả lời

24. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Đường thẳng SC tạo với đáy một góc Khi đó, thể tích của khối chóp S.ABCD bằng

$A . \frac{a^{3} \sqrt{17}}{\sqrt{3}}$

$B . \frac{a^{3} \sqrt{17}}{3}$

$C . \frac{a^{3} \sqrt{17}}{9}$

$D . \frac{a^{3} \sqrt{17}}{6}$

Xem giải thích câu trả lời

25. Nhiều lựa chọn

1 điểm • Không giới hạn

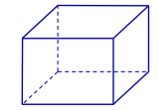
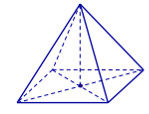
Hình đa diện nào sau đây không có mặt phẳng đối xứng

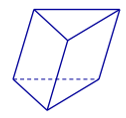
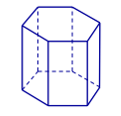
A. Hình lăng trụ lục giác đều

B. Hình lăng trụ tam giác

C. Hình chóp tứ giác đều

D. Hình lập phương

Xem giải thích câu trả lời

26. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, cạnh bên SA vuông góc với đáy và SA = a $\sqrt{2}$ . Gọi M là trung điểm của AB. Tính khoảng cách d giữa hai đường thẳng SM và BC

$A . d = \frac{a \sqrt{3}}{2}$

$B . d = \frac{a \sqrt{2}}{3}$

$C . d = \frac{a \sqrt{3}}{3}$

$D . d = \frac{a}{2}$

Xem giải thích câu trả lời

27. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy ABC là một tam giác vuông tại A, BC = 2a, $\hat{A B C} = 60^{0}$ . Gọi M là trung điểm của BC. Biết SA = SB = SM = $\frac{a \sqrt{39}}{3}$ . Tìm khoảng cách d từ S đến mặt phẳng (ABC)

A. d = 3a

B. d = a

C. d = 2a

D. d = 4a

Xem giải thích câu trả lời

28. Nhiều lựa chọn

1 điểm • Không giới hạn

Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật, có đáy là hình vuông, sao cho thể tích khối hộp được tạo thành là 8 $d m^{3}$ và diện tích toàn phần là nhỏ nhất. Tìm độ dài cạnh đáy vủa mỗi hộp được thiết kế

$A . 2 \sqrt[3]{2} d m$

$B . 2 d m$

$C . 4 d m$

$D . 2 \sqrt{2} d m$

Xem giải thích câu trả lời

29. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho tứ diện ABCD có AB = CD = $\sqrt{5}$ , AC = BD = $\sqrt{10}$ , AD = BC = $\sqrt{13}$ . Tính thể tích tứ diện đã cho

$A . 5 \sqrt{26}$

$B . \frac{5 \sqrt{26}}{6}$

C. 4

D. 2