30 câu hỏi
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng . Gọi lần lượt thể tích khối cầu và khối nón ngoại tiếp hình chóp S.ABCD. Tính tỷ số
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi M, N, P lần lượt là trung điểm của các cạnh SA, CD, CB. Tính côsin góc tạo bởi mặt phẳng (MNP) và (SCD).
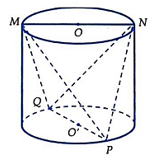
Một người thợ có một khối đá hình trụ có bán kính đáy bằng 30cm. Kẻ hai đường kính MN, PQ của hai đáy sao cho . Người thợ đó cắt khối đá theo các mặt cắt đi qua ba trong bốn điểm M, N, P,Q để được một khối đá có hình tứ diện (như hình vẽ dưới). Biết rằng khối tứ diện MNPQ có thể tích bằng . Thể tích của lượng đá bị cắt bỏ gần với kết quả nào dưới đây nhất?
111,40
111,39
111,30
111,35
Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ:
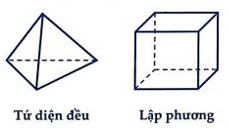


Mệnh đề nào sau đây đúng?
Mọi khối đa diện đều có số mặt là những số chia hết cho 4.
Mọi khối lập phương và khối bát diện đều có cùng số cạnh.
Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.
Khối 12 mặt đều và khối 20 mặt đều có cùng số đỉnh.
Cho hai đường thẳng phân biệt a,b và mặt phẳng (). Mệnh đề nào sau đây là đúng?
Nếu a//() và b//() thì b//a.
Nếu a//() và b thì b .
Nếu a//) và b() thì ab.
Nếu a() và ba thì .
Hình chóp đều S.ABCD. Gọi O là giao điểm của AC và BD. Phát biểu nào dưới đây là đúng?
Không tồn tại phép dời hình biến hình chóp S.ABCD thành chính nó.
Ảnh của hình chóp S.ABCD qua phép tịnh tiến theo véc-tơ là chính nó.
Ảnh của hình chóp S.ABCD qua phép đối xứng mặt phẳng (ABCD) là chính nó.
Ảnh của hình chóp S.ABCD qua phép đối xứng trục SO là chính nó.
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N). lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai
V = 13πrh
l2 = h2 + r2
Stp = πr(1+r)
Sxq = πrl
Cho hình trụ có bán kính đáy bằng a, chu vi của thiết diện qua trục bằng 12a. Thể tích của khối trụ đã cho bằng
5
6
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm của các cạnh SD, CD, BC. Thể tích khối chóp S.ABPN là x, thể tích khối tứ diện CMNP là y. Giá trị của x,y thỏa mãn các bất đẳng thức nào dưới đây?
x2 + 2xy - y2 > 160
x2 - 2xy + 2y2 < 109
x2 + xy - y4 < 145
x2 - xy + y4 > 125
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng . Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
VTVN = 26
VTVN = 23
VTVN = 32
Đáp án khác
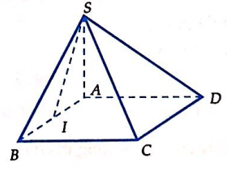
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh A. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm I thuộc đoạn AB sao cho BI = 2AI. Góc giữa mặt bên (SCD) và mặt đáy (ABCD) bằng . Tính khoảng cách giữa hai đường thẳng AD và SC.
9331a
39331a
9331
39331a
Khối đa diện nào sau đây có các mặt không phải là tam giác đều?
Bát diện đều
Nhị thập diện đều
Tứ diện đều
Thập nhị diện đều
Cho ba điểm A, B, C thẳng hang theo thứ tự đó và AB = 2BC. Dựng các hình vuông ABEF, BCGH (đỉnh của hình vuông tính theo chiều kim đồng hồ). Xét phép quay tâm B góc quay biến điểm E thành điểm A. Gọi I là giao điểm của EC và GH. Giả sử I biến thành điểm J qua phép quay trên. Nếu AC = 3 thì IJ bằng bao nhiêu?
210
5
25
10
Mệnh đề nào sau đây đúng?
Hai mặt phẳng vuông góc với nhau thì đường thẳng nào nằm trong mặt này cũng vuông góc với mặt kia.
Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
Một đường thẳng vuông góc với một trong hai mặt phẳng song song thì vuông góc với mặt phẳng kia.
Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
Cho tứ diện đều ABCD cạnh bằng a. Khoảng cách d giữa hai đường thẳng AD và BC là:
d = a32
d = a22
d = a23
d = a33
Cho khối trụ (T) có bán kính đáy bằng R và diện tích toàn phần bằng . Tính thể tích V của khối trụ (T)
V = 6πR3
V = 3πR3
V = 4πR3
V = 8πR3
Cho hình nón tròn xoay có đường cao h = 40 (cm), bán kính đáy r = 50 (cm). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 24 (cm). Tính diện tích của thiết diện
S = 800
S = 1200
S = 1600
S = 2000
Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều, độ dài cạnh AB = 2a. Hình chiếu vuông góc của A' lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng , tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACC'A')
h = 39a13
h = 215a5
h = 221a7
h = 15a5
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M,N lần lượt là trung điểm của BB', CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai phần, là thể tích của phần đa diện chứa điểm B, thể tích phần đa diện còn lại. Tính tỉ số
=
= 2
= 3
=
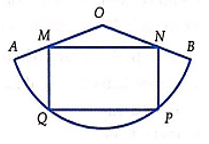
Cho tấm tôn hình nón có bán kính đáy là r = , độ dài đường sinh l = 2. Người ta cắt theo một đường sinh và trải phẳng ra được một hình quạt. Gọi M, N thứ tự là trung điểm OA và OB. Hỏi khí cắt hình quạt theo hình chử nhật MNPQ (hình vẽ) và tạo thành hình trụ đường sinh PN trùng MQ (2 đáy làm riêng) thì được khối trụ có thể tích bằng bao nhiêu?
3π(13 - 1)8
3(13 - 1)8π
5(13 - 1)12π
π(13 - 1)9
Cho tứ diện đều ABCD cạnh a. M là trung điểm cảu BC, K là điểm thuộc BD sao cho BK = 2KD. I là trung điểm của AC. Tính diện tích thiết diện tạo bởi mặt phẳng (IMK) và hình chóp.
a24
a25126
5a251144
4a29
Xét các mệnh đề sau:
(I) Có một và chỉ một đường thẳng đi qua 2 điểm phân biệt.
(II) Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt.
(III) Nếu 2 mặt phẳng có một điểm chung thì chúng có duy nhất một điểm chung khác nữa.
(IV) Nếu 1 đường thẳng có 2 điểm phân biệt thuộc mặt phẳng thì mọi điểm của đường thẳng đó đều thuộc mặt phẳng.
Số mệnh đề sai là:
1.
2.
3.
4.
Cho hình lăng trụ ABC.A’B’C’ độ dài cạnh bên là 2a, dáy ABC là tam giác vuông tại A, AB = a, AC = . Hình chiếu của A’ lên (ABC) trùng với trung điểm I của BC. Khi đó cos(AA';B'C') là:
12
14
22
32
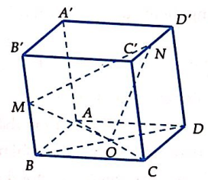
Cho hình hộp ABCD.A’B’C’D’, O = ACBD, M, N lần lượt là trung điểm cảu BB’ và C’D’. Mặt phẳng (MNO) cắt B’C’ tại E thì tỉ số là:
75
23
13
12
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh 2a, SA = và vuông góc với đáy, I là trung điểm của AB. Tính khoảng cách giữa SI và BC.
d(SI;BC) = a
d(SI;BC) = a34
d(SI;BC) = a3
d(SI;BC) = a32
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm BC và BD. Khi đó gọi là thể tích cảu ABCD và là thể tích của ABMN thì tỉ số là:
14
12
18
13
Trong các khối trụ có thể tích V không đổi thì hình trụ có diện tích toàn phần lớn nhất khi tỉ lệ giữa chiều cac h và bán kính đáy R là:
hR = 1
hR = 2
hR = 2
hR = 12
Chia tấm bìa hình tròn bán kính cm thành 3 phần (như hình vẽ). lấy một phần và uốn thành một hình nón có đường sinh là bán kính của hình tròn trên. Khi đó thể tích của khối nón tạo thành là:
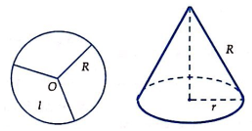
2πR3281
πR327
2πR3227
πR381
Cho tứ diện ABCD có AB = 3a, AC = 5a, AD = 4a, các góc . Khi đó thể tích khối ABCD là:
5a33
5a32
a32
10a32
Cho hình chóp đều S.ABC, đáy ABC cạnh a, . Gọi D là điểm đối xứng với B qua C. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABD.
R = a
R =
R =
R =








