30 câu hỏi
Tứ diện OABC, có OA = a, OB = b, OC = c và đôi một vuông góc với nhau. Thể tích khối tứ diện OABC bằng
abc3
abc
abc6
abc2
Một khối chóp có thể tích bằng và chiều cao bằng 2a. Diện tích mặt đáy của khối chóp là
B = 6a22
B = 6a2
B = 6a4
B = 6a
Tính thể tích của khối lập phương ABCD.A'B'C'D' biết AD' = 2a
V =
V = 8
V =
V =
Cho khối hộp ABCD.A'B'C'D'. Mặt phẳng (P) đi qua trung điểm của AB, A'D' và CC' chia khối hộp thành hai đa diện. Khối chứa đỉnh D có thể tích là , khối chứa đỉnh B có thể tích là Khi đó ta có
V1V2 = 12
V1V2 = 34
V1V2 = 1
V1V2 = 13
Cho môt tấm tôn hình chữ: nhật ABCD có AD = 60 cm. Ta gấp tấm tôn theo 2 cạnh MN và QP vào phía trong sao cho BA trùng với CD(như hình vẽ) để được lăng trụ đứng khuyết hai đáy. Khối lăng trụ có thể tích lớn nhất khi x bằng bao nhiêu?
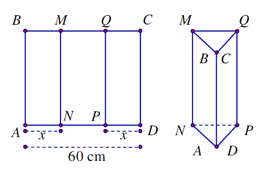
x = 20
x = 30
x = 45
x = 40
Cho tứ diện ABCD có các cạnh BA, BC, BC đôi một vuông góc với nhau, BA = 3a, BC = BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM
V = 8
V =
V =
V =
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc cạnh AB sao cho HB = 2HA. Cạnh SC tạo với mặt phẳng đáy (ABCD) một góc bằng . Khoảng cách từ trung điểm K của HC đến mặt phẳng (SCD) là
a132
a134
a13
a138
Hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; biết AB = AD = 2a, CD = a. Gọi I là trung điểm của AD, biết hai mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD), Thể tích khối chóp S.ABCD bằng . Góc giữa hai mặt phẳng (SBC) và (ABcD) bằng
900
600
300
450
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Gọi M là trung điểm của CD. Khoảng cách từ M đến mặt phẳng (SAB) là:
a22
a
a2
2a
Cho hình chóp S.ABCD đáy là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA vuông góc với đáy, SA = a. Gọi M, N lần lượt là trung điểm của SB, CD. Tính côsin góc giữa MN và (SAC)
15
3510
5510
25
Từ một tấm tôn có kích thước 90cm x 3m, người ta làm một máng xối nước trong đó mặt cắt là hình thang ABCD có hình dưới. Tính thể tích lớn nhất của máng xối.
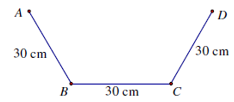
405006 cm3
405005 cm3
2025003 cm3
405002 cm3
Tìm số mặt phẳng đối xứng của tứ diện đều.
4
9
3
6
Cho hình lăng trụ đứng ABC.A'B'C'. Cạnh bên AA' = a, ABC là tam giác vuông tại A có BC = 2a, AB = a. Tính khoảng cách từ đỉnh A đến mặt phẳng (A'BC)
a217
a2121
a37
a721
Cho hình chóp tam giác S.ABC có , SA = SB = a, SC = 3a. Tính thể tích của khối chóp ?
a328
a324
a3212
a323
Cho khối chóp tam giác đều S.ABC có thể tích là , AB = a. Tính theo a khoảng cách từ S tới mặt phẳng (ABC)
2a3
2a3
4a6
a3
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE = 2EC. Tính thể tích V của khối tứ diện SEBD.
V =
V =
V =
V =
Trong các mặt của khối đa diện, số cạnh cùng thuộc một mặt tối thiểu là
5
4
3
2
Cho lăng trụ tứ giác đều có tất cả các cạnh bằng nhau và biết tổng diện tích các mặt của lăng trụ bằng 296cm . Tính thể tích khối lăng trụ.
128
64
32
60
Các trung điểm của tất cả các cạnh của hình tứ diện đều là các đỉnh của
Hình lập phương.
Hình bát diện đều.
Hình tứ diện đều.
Hình hộp chữ nhật.
Hình nào dưới đây không phải là hình đa diện ?
Hình trụ.
Hình lập phương.
Hình chóp.
Hình bát diện đều.
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a, BC = a, biết SA = a và vuông góc với mặt phẳng đáy. Một mặt phẳng () đi qua A , vuông góc với SC tại H , cắt SB tại K . Tính thể tích khối chóp S.AHK theo a
a3330
5a3360
a3360
a3310
Phát biểu nào sau đây là đúng?
Hình hai mươi mặt đều có 20 đỉnh, 30 cạnh, 12 mặt
Hình hai mươi mặt đều có 30 đỉnh, 12 cạnh, 20 mặt.
Hình hai mươi mặt đều có 30 đỉnh, 20 cạnh, 12 mặt.
Hình hai mươi mặt đều có 12 đỉnh, 30 cạnh, 20 mặt.
Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a và thể tích khối chóp bằng . Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBC)
a62
a63
a66
a6
Thể tích khối tứ diện đều ABCD có cạnh bằng là:
V =
V =
V =
V =
Tính tổng diện tích các mặt của một khối bát diện đều cạnh a .
2a33
a3316
8a23
8a2
Hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 3cm, BC = 4 cm, SC = 5 cm. Tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với (ABCD). Các mặt (SAB) và (SAC) tạo với nhau một góc sao cho = . Tính thể tích khối chóp S.ABCD
16 cm2
1529 cm2
20 cm2
185 cm2
Tính thể tích khối lập phương ABCD.A'B'C'D' biết độ dài đoạn thẳng AC = 2a.
2a323
2a32
a3
a33
Trong các mệnh đề sau, mệnh đề nào sai?
Nếu hai mặt phẳng có một điểm chung thì chúng còn có vô số các điểm chung khác nữa.
Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.
Nếu một đường thẳng cắt một trong hai mặt phẳng song song với nhau thì cắt mặt phẳng còn lại.
Nếu hai đường thẳng phân biệt cùng song song với một mặt phẳng thì chúng song song với nhau.
Một khối đa diện lồi với các mặt là tam giác thì:
3M = 2C
3M > 2C
3M < 2C
cả 3 đáp án sai
Trong các mệnh đề sau, mệnh đề nào sai?
Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với đường thẳng còn lại.
Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng thì song song với nhau.








