30 câu hỏi
Cho hình chóp tứ giác S.ABCD có M, N, P, Q lần lượt là trung điểm các cạnh SA, SB, SC, SD. Biết khối chóp S.ABCD có thể tích bằng 16. Tính thể tích khối chóp S.MNPQ theo a
2
8
4
Tính thể tích khối chóp tứ giác đều có cạnh đáy bằng 2a và diện tích của một mặt bên là
4a323
4a33
4a3
4a333
Cho hình trụ có bán kính đáy bằng 3 cm, độ dài đường cao bằng 4 cm. Tính diện tích xung quanh của hình trụ này.
24
22
26
20
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, hai mặt phẳng (SAB), (SAD) cùng vuông góc với đáy, SC tạo với đáy góc . Tính thể tích khối chóp S.ABCD theo a.
a323
a363
2a363
4a363
Cho tứ diện SABC có ABC là tam giác vuông cân tại A, đường cao SA. Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng .Tính theo a thể tích khối tứ diện SABC
a363
a333
2a363
a323
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Điểm M thuộc đoạn thẳng BC' , điểm N thuộc đoạn thẳng AB' tạo với mặt phẳng đáy một góc . Tìm độ dài nhỏ nhất của đoạn thẳng MN.
a2
2a3
2a5 - 1
2a5 + 1
Tính thể tích chóp S.ABCD có đáy là hình vuông cạnh bằng a, mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy.
a332
a33
a333
a336
Tính thể tích của một khối tứ diện đều cạnh bằng a
a3224
a3212
a336
a3312
Cho khối chóp S.ABC có các điểm A', B', C' lần lượt thuộc các cạnh SA, SB, SC thỏa 3SA' = SA, 4SB' = SB, 5SC' = 3SC. Biết thể tích khối chóp S.A'B'C' bằng 5 (). Tìm thể tích khối chóp S.ABC
120 ()
60 ()
80 ()
100 ()
Cho hình nón tròn xoay có đường cao là a, đường kính đáy là 2a. Tìm diện tích xung quanh của hình nón đã cho.
23πa2
2πa2
πa2
43πa2
Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách từ đỉnh B đến mặt phẳng (ACD).
a62
a32
a63
a23
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy là hình bình hành. Các đường chéo DB' và AC' lần lượt tạo với đáy các góc. Biết chiều cao của lăng trụ là a và , hãy tính thể tích V của khối lăng trụ này.
V = a323
V = a33
V = a32
V = a332
Tính thể tích của một khối lăng trụ tam giác đều ABC.A'B'C' có AC' bằng 5a, đáy là tam giác đều cạnh bằng 4a
12
20
20
12
Cho một tứ diện có đúng một cạnh có độ dài bằng x thay đổi được, các cạnh còn lại có độ dài bằng 2. Tính giá trị lớn nhất của thể tích tứ diện này.
12
223
332
1
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AD = a, AB = 2a, BC = 3a, SA = 2a. H là trung điểm cạnh AB, SH là đường cao của hình chóp S.ABCD, Tính khoảng cách từ điểm A đến mp (SCD)
a307
a3010
a1310
a137
Tính chiều dài nhỏ nhất của cái thang để nó có thể dựa vào tường và mặt đất, bắc ngang qua cột đỡ cao 4m. Biết cột đỡ song song và cách tường 0,5m mặt phẳng chứa tường vuông góc với mặt đất- như hình vẽ, bỏ qua đội dày của cột đỡ.
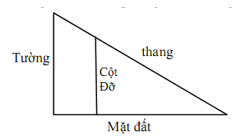
532
552
332
352
Tính thể tích của khối lập phương có diện tích một mặt chéo bằng .
22a3
a3
2a3
42a3
Cho khối tứ diện ABCD có thể tích bằng V, thể tích của khối đa diện có đỉnh là trung điểm các cạnh của tứ diện ABCD bằng V'. Tính tỉ số
=
=
=
=
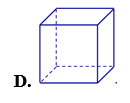
Hình nào dưới đây không phải là hình đa diện?
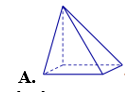
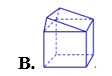
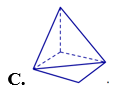
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a, góc giữa đường thẳng AC' và mặt phẳng đáy bằng . Tính thể tích khối lăng trụ ABC.A'B'C' theo a.
3a34
a312
3a34
a34
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ B đến (SCD)
1
Chọn khẳng định sai. Trong một khối đa diện
Mỗi đỉnh là đỉnh chung của ít nhất mặt.
Mỗi mặt có ít nhất cạnh.
Mỗi cạnh của khối đa diện là cạnh chung của đúng mặt.
Hai mặt bất kì luôn có ít nhất một điểm chung.
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a, SA = . Tính thể tích V của khối chóp S.ABC
V = 35a324
V = 3a36
V = 2a36
V = 2a32
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại với AB = a, BC = 2a.
Điểm H thuộc cạnh AC sao cho CH = CA, SH là đường cao hình chóp S.ABC và SH = . Gọi I là trung điểm BC. Tính diện tích thiết diện của hình chóp S.ABC với mặt phẳng đi qua H và vuông góc với AI
22a23
2a26
3a23
3a26
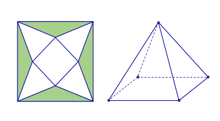
Cho một tấm nhôm hình vuông cạnh 1 (m) như hình vẽ dưới đây. Người ta cắt phần tô đậm của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng x (m). Tìm giá trị của x để khối chóp nhận được có thể tích lớn nhất.
x = 24
x = 23
x = 225
x = 12
Tứ diện đều có bao nhiêu mặt phẳng đối xứng?
2
3
6
9
Cho lăng trụ ABC.A'B'C' có các mặt bên là hình vuông cạnh a. Gọị D,E lần lượt là trung điểm các cạnh BC, A'C'. Tính khoảng cách giữa hai đường thẳng AB' và DE theo a
a33
a34
a32
a3
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Góc giữa mặt phẳng (SBC) và (ABCD) bằng . Gọi M, N lần lượt là trung điểm của AB, AD. Tính thể tích khối chóp S.CDMN theo a
5a38
a38
5a324
a33
Cho hình chóp S.ABCD có cạnh SA = x còn tất cả các cạnh khác có độ dài bằng 2. Tính thể tích lớn nhất của khối chóp S.ABCD
V = 1
V =
V = 3
V = 2
Cho hình lăng trụ đứng ABC.A'B'C', đáy ABC là tam giác vuông tại A, cạnh AA' hợp với B'C một góc và khoảng cách giữa chúng bằng a, B'C = 2a. Thể tích của khối lăng trụ ABC.A'B'C' theo a
a32
3a32
3a34
a34








