Quiz

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P1)

Admin30 câu hỏiToánLớp 11

30 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N, I là 3 điểm lấy trên AD, CD, SO. Thiết diện của hình chóp với mặt phẳng (MNI) là:

A. Một tam giác

B. Tứ giác

C. Ngũ giác

D. Lục giác

Xem giải thích câu trả lời

2. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình lăng trụ đứng ABC.A'B'C' đáy ABC là tam giác đều, I là trung điểm của AB. Kí hiệu d(AA',BC) là khoảng cách giữa 2 đường thẳng AA' và BC thì:

A. d(AA',BC) = AB

B. d(AA',BC) = IC

C. d(AA',BC) = A'B

D. d(AA',BC) = AC

Xem giải thích câu trả lời

3. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho tứ diện ABCD và điểm G thỏa mãn $\overset{⇀}{G A} + \overset{⇀}{G B} + \overset{⇀}{G C} + \overset{⇀}{G D} = \overset{⇀}{0}$ (G gọi là trọng tâm của tứ diện). Gọi $G_{A} = G A \cap (B C D)$ . Trong các khẳng định sau, khẳng định nào đúng?

A. $\overset{⇀}{G A} = - 3 \overset{⇀}{G_{A} G}$

B. $\overset{⇀}{G A} = 4 \overset{⇀}{G_{A} G}$

C. $\overset{⇀}{G A} = 3 \overset{⇀}{G_{A} G}$

D. $\overset{⇀}{G A} = 2 \overset{⇀}{G_{A} G}$

Xem giải thích câu trả lời

4. Nhiều lựa chọn

1 điểm • Không giới hạn

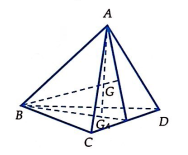
Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc. Gọi H là hình chiếu của O lên (ABC). Xét các mệnh đề sau:

I. H là trực tâm của $∆$ ABC.

II. H là trọng tâm của $∆$ ABC.

III. $\frac{1}{O H^{2}} = \frac{1}{O A^{2}} + \frac{1}{O B^{2}} + \frac{1}{O C^{2}}$

Số mệnh đề đúng là:

A. 0

B. 1

C. 2

D. 3

Xem giải thích câu trả lời

5. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại B. BC = a, $\hat{A B C}$ = $60^{0}$ , CC' = 4a. Tính thể tích khối A'CC'B'B.

A. $a = \frac{2 a^{3} \sqrt{3}}{3}$

B. $a = \frac{a^{3} \sqrt{3}}{3}$

C. $a = a^{3} \sqrt{3}$

D. $a = 3 a^{3}$

Xem giải thích câu trả lời

6. Nhiều lựa chọn

1 điểm • Không giới hạn

Kim tự tháp Kê – ốp ở Ai Cập được xây dựng và khoảng 2500 năm trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao là 147 m, cạnh đáy là 230 m. Thể tích của nó là:

A. 2592100 m³

B. 2952100 m³

C. 2529100 m³

D. 2591200 m³

Xem giải thích câu trả lời

7. Nhiều lựa chọn

1 điểm • Không giới hạn

Hình tứ diện có số mặt đối xứng là:

A. 3

B. 4

C. 6

D. 9

Xem giải thích câu trả lời

8. Nhiều lựa chọn

1 điểm • Không giới hạn

Một khối trụ có đường kính đáy bằng chiều cao và nội tiếp trong mặt cầu bán kính R thì thể tích của khối trụ là:

A. $2 {πR}^{3}$

B. $\frac{{πR}^{3} \sqrt{2}}{2}$

C. $\frac{{πR}^{3} \sqrt{2}}{6}$

D. $\frac{2 {πR}^{3}}{3}$

Xem giải thích câu trả lời

9. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABCD đáy ABCD là hình chữ nhật cạnh AB = 2a, AD = a, $∆ S A D$ đều và nằm trong mặt phẳng vuông góc với đáy. Diện tích xung quanh của mặt cầu ngoại tiếp hình chóp S.ABCD là:

A. $\frac{16 π}{3} a^{2}$

B. $\frac{57 π}{18} a^{2}$

C. $\frac{48 π}{9} a^{2}$

D. $\frac{24 π}{9} a^{2}$

Xem giải thích câu trả lời

10. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho tứ diện đều ABCD. Biết khoảng cách từ điểm A đến mặt phẳng (BCD) bằng 6. Tính thể tích của tứ diện ABCD

A. $V = 27 \sqrt{3}$

B. $V = 5 \sqrt{3}$

C. $V = \frac{27 \sqrt{3}}{2}$

D. $V = \frac{9 \sqrt{3}}{2}$

Xem giải thích câu trả lời

11. Nhiều lựa chọn

1 điểm • Không giới hạn

Thể tích khối cầu tâm I, có bán kính 2R bằng

A. $V = \frac{4}{3} {πR}^{3}$

B. $V = \frac{1}{3} {πR}^{3}$

C. $V = \frac{32}{3} {πR}^{3}$

D. $V = \frac{8}{3} {πR}^{3}$

Xem giải thích câu trả lời

12. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có $\hat{B A C} = 75^{0}, \hat{A C B} = 60^{0}$ . Kẻ BH $⊥$ AC. Quay quanh AC thì $∆$ BHC tạo thành hình nón tròn xoay (N). Tính diện tích xung quanh của hình nón xoay (N) theo R.

A. $\frac{3 + 2 \sqrt{2}}{2} {πR}^{2}$

B. $\frac{3 + 2 \sqrt{3}}{2} {πR}^{2}$

C. $\frac{\sqrt{3} (1 + \sqrt{2})}{4} {πR}^{2}$

D. $\frac{\sqrt{3} (1 + \sqrt{3})}{4} {πR}^{2}$

Xem giải thích câu trả lời

13. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, SA = SB = SC. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng $45^{0}$ . Tính khoảng cách từ điểm S đến mặt phẳng (ABC)

A. $\frac{a \sqrt{3}}{3}$

B. $\frac{a \sqrt{2}}{2}$

C. $a \sqrt{2}$

D. $a \sqrt{3}$

Xem giải thích câu trả lời

14. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết thể tích của khối lăng trụ là $\frac{a^{3} \sqrt{3}}{4}$ . Tính khoảng cách giữa hai đường thẳng AA' và BC

A. $\frac{4 a}{3}$

B. $\frac{2 a}{3}$

C. $\frac{3 a}{4}$

D. $\frac{3 a}{2}$

Xem giải thích câu trả lời

15. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân đỉnh C, A'C = a. Gọi x là góc giữa hai mặt phẳng (A'CB) và (ABC) để thể tích khối chóp A'.ABC lớn nhất. Tính thể tích lớn nhất của khối chóp A'.ABC theo a

A. $\frac{a^{3} \sqrt{3}}{3}$

B. $\frac{a^{3} \sqrt{3}}{9}$

C. $\frac{a^{3} \sqrt{3}}{27}$

D. $\frac{a^{3} \sqrt{3}}{81}$

Xem giải thích câu trả lời

16. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình hộp ABCD.A'B'C'D'. Gọi I và I' lần lượt là tâm của ABB'A' và DCC'D'. Mệnh đề nào sau đây là sai?

$A . \overset{⇀}{I I'} = \overset{⇀}{A D}$

B. II'//(ADD'A')

C. II' và BB' cùng nằm trong một mặt phẳng

D. II' và DC không có điểm chung

Xem giải thích câu trả lời

17. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình lập phương ABCD.A'B'C'D'. Tính số đo góc giữa hai mặt phẳng (BA'C) và (DA'C). Tính số đo góc giữa hai mặt phẳng (BA'C) và (DA'C).

A. 60°

B. 135°

C. 150°

D. 90°

Xem giải thích câu trả lời

18. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA = 3HB. Góc giữa đường thẳng SC và mặt phẳng bằng 60°. Tính khoảng cách giữa hai đường thẳng SA và BC theo a.

$A . \frac{a \sqrt{61}}{4}$

$B . \frac{4 a \sqrt{17}}{3}$

$C . \frac{a \sqrt{35}}{51}$

$D . \frac{4 a \sqrt{351}}{3 \sqrt{61}}$

Xem giải thích câu trả lời

19. Nhiều lựa chọn

1 điểm • Không giới hạn

Cắt khối nón bởi mặt phẳng qua trục tạo thành tam giác ABC đều cạnh a. Biết B, C thuộc đường tròn đáy. Thể tích của khối nón là

$A . \frac{3 a^{3} π \sqrt{3}}{4}$

$B . \frac{a^{3} π \sqrt{3}}{12}$

$C . \frac{a^{3} π \sqrt{3}}{24}$

$A . \frac{a^{3} 2 \sqrt{3}}{9}$

Xem giải thích câu trả lời

20. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy ABC là tam giác đều có cạnh là a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc vơi đáy. Tính thể tích của khối cầu ngoại tiếp hình chóp.

$A . \frac{\sqrt{15} {πa}^{3}}{9}$

$B . \frac{5 \sqrt{15} {πa}^{3}}{54}$

$C . \frac{5 \sqrt{15} {πa}^{3}}{18}$

$D . \frac{4 \sqrt{3} {πa}^{3}}{27}$

Xem giải thích câu trả lời

21. Nhiều lựa chọn

1 điểm • Không giới hạn

Một phễu đựng kem hình nón bằng bạc có thể tích $12 π$ (cm³) và chiều cao là 4 cm. Muốn tăng thể tích kem trong phễu hình nón lên 4 lần nhưng chiều cao không thay đổi thì diện tích miếng giấy bạc cần thêm là

$A . (12 \sqrt{13} - 15) π ({cm}^{2})$

$B . 12 π \sqrt{13} ({cm}^{2})$

$C . \frac{12 \sqrt{13}}{15} ({cm}^{2})$

$D . (12 \sqrt{13} + 15) π ({cm}^{2})$

Xem giải thích câu trả lời

22. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy (ABCD), SC = $a \sqrt{5}$ . Tính thể tích khối chóp.

$A . V = \frac{a^{3} \sqrt{3}}{3}$

$B . V = \frac{a^{3} \sqrt{3}}{6}$

$C . V = a^{3} \sqrt{3}$

$D . V = \frac{a^{3} \sqrt{3}}{9}$

Xem giải thích câu trả lời

23. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh là 1. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng $\frac{\sqrt{3}}{4}$ , tính thể tích V của khối lăng trụ.

$A . V = \frac{\sqrt{3}}{36}$

$B . V = \frac{\sqrt{3}}{3}$

$C . V = \frac{\sqrt{3}}{6}$

$D . V = \frac{\sqrt{3}}{12}$

Xem giải thích câu trả lời

24. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho một chiếc cốc thủy tinh có hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần lượt là 20 cm và 5 cm. Người ta đặt cái cốc vào trong một hộp có dạng hình hộp chữ nhật sao cho cái cốc vừa khít trong hộp. Tính thể tích chiếc hộp đó.

$A . 500 \sqrt{3}$ cm³

$B . 1000 \sqrt{3}$ cm³

$C . 750 \sqrt{3}$ cm³

$D . 100 \sqrt{3}$ cm³

Xem giải thích câu trả lời

25. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho mặt cầu (S) có tâm O và bán kính R. Diện tích mặt cầu (S) được cho bởi công thức nào trong các công thức dưới đây?

$A . 4 {πR}^{2}$

$B . 4 R^{2}$

$C . \frac{4}{3} {πR}^{2}$

$D . {πR}^{2}$

Xem giải thích câu trả lời

26. Nhiều lựa chọn

1 điểm • Không giới hạn

Trong không gian cho tam giác ABC vuông tại A có AB = 2a và BC = 2a. Quay tam giác ABC xung quanh cạnh AB ta thu được khối nón có thể tích bằng

$A . {πa}^{3}$

$B . 3 π a^{3}$

$C . \frac{\sqrt{3}}{3} {πa}^{3}$

$D . \frac{2}{3} {πa}^{3}$

Xem giải thích câu trả lời

27. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = 3a. Chọn hệ trục tọa độ Oxyz sao cho A trùng với O, điểm B thuộc tia Ox, điểm D thuộc tia Oy và điểm S thuộc tia Oz. Gọi G là trọng tâm của tam giác SBD. Mệnh đề nào dưới đây là đúng?

$A . G (\frac{a}{3}; \frac{a}{3}; a)$

$B . G (a; a; 3 a)$

$C . G (\frac{a}{2}; \frac{a}{2}; \frac{3 a}{2})$

$D . G (\frac{a}{3}; a; \frac{a}{3})$

Xem giải thích câu trả lời

28. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình lập phương ABCD.A'B'C'D'. Gọi $α$ là góc giữa đường thẳng AC’ với mặt phẳng (ABCd). Mệnh đề nào dưới đây đúng?

$A . \frac{2 π}{9} \leq α \leq \frac{π}{4}$

$B . \frac{π}{4} < α < \frac{π}{3}$

$C . \frac{π}{6} < α < \frac{2 π}{9}$

$D . \frac{π}{9} \leq α \leq \frac{π}{6}$

Xem giải thích câu trả lời

29. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SA vuông góc với mặt phẳng (ABC). Biết rằng AB = a, AC = a $\sqrt{3}$ và $\hat{S B A} = 60^{0}$ . Gọi H là hình chiếu vuông góc của A trên cạnh SC. Tính tỷ số thể tích của hai khối SABH và HABC.

$A . \frac{3}{4}$

$B . \frac{1}{12}$

$C . \frac{3}{2}$

$D . \frac{7}{4}$

Xem giải thích câu trả lời

30. Nhiều lựa chọn

1 điểm • Không giới hạn

Cho hình lăng trụ đều ABC.A'B'C' có góc giữa đường thẳng A'B với mặt phẳng (ABC) bằng $60^{0}$ và khoảng cách từ điểm A đến mặt phẳng (A'BC) bằng $\frac{a \sqrt{5}}{2}$ . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.

$A . V = \frac{125 \sqrt{3}}{96} a^{3}$

$B . V = \frac{125 \sqrt{3}}{288} a^{3}$

$C . V = \frac{125 \sqrt{3}}{384} a^{3}$

$D . V = \frac{125 \sqrt{3}}{48} a^{3}$

Xem giải thích câu trả lời