25 câu hỏi
Cho hàm số y = . Tìm giá trị lớn nhất của tham số thực m để hàm số đã cho đồng biến trên .
m = 2
m = 3
m = 4
m = 1
Giá trị lớn nhất của biểu thức P = bằng
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số y = có hai điểm cực trị nằm trong khoảng .
2015
2016
2018
4035
Công ty du lịch Ban Mê dự định tổ chức tua xuyên Việt. Công ty dự định nếu giá tua là 2 triệu đồng thì sẽ có khoảng 150 người tham gia. Để kích thích mọi người tham gia. Hỏi công ty phải bán giá tua là bao nhiêu để doanh thu từ tua xuyên Việt là lớn nhất.
1375000.
3781250.
2500000.
3000000.
Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng (-10000;10000) để hàm số y = đồng biến trên khoảng ?
999.
1001.
1998.
1000.
Hàm số f(x) có đạo hàm f'(x) trên khoảng K. Hình vẽ bên là đồ thị của hàm số f'(x) trên khoảng K. Hỏi hàm số f(x) có bao nhiêu điểm cực trị?
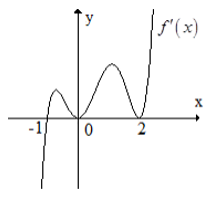
0
4
3
1
Cho hàm số y = f(x) xác định trên và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + m - 2018 = 0 có duy nhất một nghiệm.
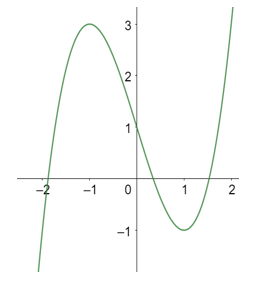
m 2015, m 2019.
2015 < m < 2019.
m = 2015, m = 2019.
m < 2015, m > 2019.
Đồ thị hàm số y = có tất cả bao nhiêu đường tiệm cận?
4
3
1
2
Hàm số y = đồng biến trên khoảng nào dưới đây?
(0;2)
(0;+)
(-;-2)
(-;0)
Đường cong ở hình dưới là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
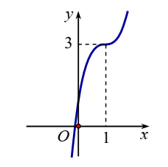
y =
y =
y =
y =
Đồ thị hàm số y = có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
x = 1 và y = 2
x = 2 và y = 1
x = 1 và y = -3
x = -1 và y = 2
Giá trị của m làm cho phương trình có hai nghiệm dương phân biệt là
m > 6
m < 6 và m 2
2 < m < 6 hoặc m < -3
m < 0 hoặc 2 < m < 6
Cho hàm số y = f(x) đồng biến trên khoảng (a;b). Mệnh đề nào sau đây sai?
Hàm số y = f(x) +1 đồng biến trên khoảng (a;b)
Hàm số y = -f(x) + 1 nghịch biến trên khoảng (a;b).
Hàm số y = f(x) +1 đồng biến trên khoảng (a;b).
Hàm số y = -f(x) -1 nghịch biến trên khoảng (a;b)
Hàm số nào sau đây đạt cực tiểu tai điểm x = 0.
y =
y =
y =
y =
Cho hàm số y = f(x) xác định trên và có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
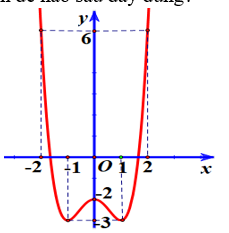
Hàm số đồng biến trên mỗi khoảng (-1;0) và (1;+)
Hàm số đồng biến trên mỗi khoảng (-;-1) và (0;1).
Hàm số nghịch biến trên khoảng (-1;1).
Hàm số nghịch biến trên mỗi khoảng (-1;0) và (1;+).
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị y = f'(x) như hình vẽ.
Xét hàm số g(x) = f(-2).

Mệnh đề nào sau đây sai?
Hàm số g(x) nghịch biến trên (0;2).
Hàm số g(x) đồng biến trên (2;+).
Hàm số g(x) nghịch biến trên (-;-2).
Hàm số g(x) nghịch biến trên (-1;0).
Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng
-2 m < -1 hoặc m > 1
m -1 hoặc m > 1
-1 < m < 1
m < -1 hoặc m 1
Cho hàm số y = có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng ?
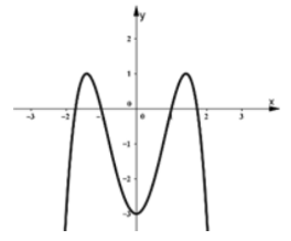
a > 0, b < 0, c < 0.
a < 0, b < 0, c < 0.
a < 0, b > 0, c < 0.
a > 0, b < 0, c > 0.
Gọi S là tập các giá trị dương của tham số m sao cho hàm số y = đạt cực trị tại thỏa mãn . Biết S = (a;b]. Tính T = 2b - a.
T = + 6
T = + 3
T = - 3
T = - 6
Cho hàm số có đồ thị (C): y = . Gọi M là điểm bất kì thuộc đồ thị (C). Gọi tiếp tuyến của đồ thị (C) tại M cắt các tiệm cận của (C) tại hai điểm P và Q. Gọi G là trọng tâm tam giác IPQ(với I là giao điểm của hai đường tiệm cận của (C)). Diện tích tam giác GPQ là
2
4
1
Tìm tất cả các giá trị thực của tham số m sao cho phương trình có hai nghiệm thực phân biệt.
-3 m < 1
-2 < m
-1 m
0 m <
Cho hai số thực x, y thay đổi thỏa mãn điều kiện . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = . Giá trị của của M + m bằng
-4
-
-6
1 - 4
Đường dây điện 110 KV kéo từ trạm phát ( điểm A) trong đất liền ra đảo ( điểm C). Biết khoảng cách ngắn nhất từ C đến B là 60 km, khoảng cách từ A đến B là 100 km, mỗi km dây điện dưới nước chi phí là 100 triệu đồng, chi phí mỗi km dây điện trên bờ là 60 triệu đồng. Hỏi điểm G cách A bao nhiêu km để mắc dây điện từ A đến G rồi từ G đến C chi phí thấp nhất? (Đoạn AB trên bờ, đoạn GC dưới nước )
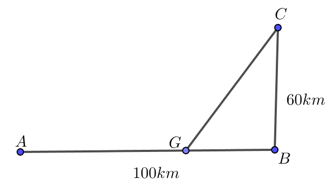
50 (km)
60 (km)
55 (km)
45 (km)
Tập hợp các giá trị của m để hàm số y = || có điểm cực trị là:
(0;6)
(6;33)
(1;33)
(1;6)
Tính tổng tất cả các nghiệm của phương trình cos2x - = trên đoạn [1;70]
188
263
363
365








