30 câu hỏi
Đồ thị hàm số y = có tiệm cận đứng là đường thẳng
y = 1
x = 1
x = 2
x = -1
Cho hàm số y = có đồ thị là (C) và điểm A. Biết có ba điểm thuộc sao cho tiếp tuyến của tại mỗi điểm đó đều đi qua A. Tính S =
S =
S =
S =
S =
Cho hàm số y = . Xác định m để đường thẳng y = mx + m - 1 luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc hai nhánh của đồ thị
m < 1
m > 0
m < 0
m = 0
Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y = || trên đoạn [-2;4] bằng 16. Số phần tử của S là
0.
2.
4.
1.
Gọi S là tập hợp các giá trị của tham số m sao cho giá trị lớn nhất của hàm số trên đoạn [-2;4] bằng 16. Số phần tử của S là
0.
2.
4.
1.
Biết rằng đồ thị hàm số y = (m,n là tham số) nhận trục hoành làm tiệm cận ngang và trục tung làm tiệm cận đứng. Tính tổng m - 2n
0.
– 3.
– 9.
6.
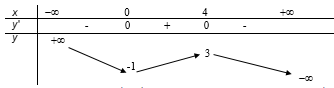
Bảng biến thiên sau là của hàm sô nào?
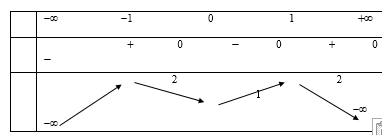
y =
y =
y =
y =
Phương trình có hai nghiệm âm phân biệt
m ∈ 59;1∪6;+∞
m ∈ -2;6
m ∈ 6;+∞
m ∈ -2;1
Tìm tập giá trị T của hàm số y =
T = [1;9]
T = [0;2]
T = (1;9)
T = [2;4]
Cho ABC có A(2;-1), B(4;5), C(-3;2). Phương trình tổng quát của đường cao BH là
3x + 5y - 37 = 0
5x - 3y - 5 = 0
3x - 5y - 13 = 0
3x + 5y - 20 = 0
Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình vẽ dưới đây

Tìm m để hàm số y = f(-2m) có ba điểm cực trị
m (-;0]
m (3;+)
m [0;]
m (-;0)
Giá trị m để hàm số y = nghịch biến trên là
m 0 hoặc 1 m < 2
1 m < 2
m 0
m > 2
Tập xác định của hàm số là
Cho hàm số y = f(x) có đồ thị f'(x) như hình vẽ bên dưới. Hàm số y = f(3-2x) nghịch biến trên khoảng nào trong các khoảng sau?
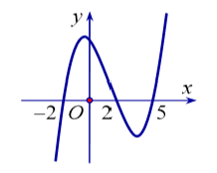
(1;+)
(0;2)
(-;-1)
(1;3)
Trong hai hàm số f(x) = và g(x) = . Hàm số nào nghịch biến trên khoảng ?
Không có hàm số nào cả.
Chỉ g(x)
Cả f(x), g(x)
Chỉ f(x)
Tìm số điểm cực trị của đồ thị hàm số y = ?
4.
1.
0.
3.
Cho hàm số y = f(x) có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
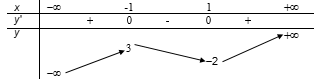
(-1;+)
(-1;1)
(-;1)
(1;+)
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên đoạn [-2;1]. Tính M + m.
0.
-9.
-10.
-1.
Tìm m để hàm số y = liên tục trên
-
-
Gọi d là tiếp tuyến tại điểm cực đại của đồ thị hàm số y = . Mệnh đề nào dưới đây đúng?
d có hệ số góc âm.
d song song với đường thẳng x = 3.
d có hệ số góc dương.
d dong dong với đường thẳng y = 3.
Trong các mệnh đề sau, mệnh đề nào sai?
Hàm số y = ln là hàm số chẵn.
Tập giá trị của hàm số y = ln là
Hàm số y = ln có tập xác định là
Giá trị của m để phương trình có ba nghiệm phân biệt lập thành một cấp số cộng thuộc khoảng nào trong các khoảng dưới đây?
(2;4).
(-2;0).
(0;2).
(-4;2).
Cho hàm số y = có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
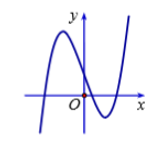
a < 0, b < 0, c < 0, d < 0
a > 0, b > 0, c < 0, d > 0
a > 0, b < 0, c < 0, d > 0
a > 0, b < 0, c > 0, d > 0
Tìm số đường tiệm cận đứng của đồ thị hàm số y =
3.
1.
0.
2.
Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây. Tìm tất cả các giá trị của m để phương trình f() = có 4 nghiệm thực phân biệt.
m (0;8).
m (;8).
m (-1;3).
m (0;).
Tìm tất cả các giá trị của m để hàm số đồng biến trên ?
m (-;-4)
m (-;-4) (4;+)
m [4;+)
m (4;+)
Cho hàm số y = f(x) có đúng ba điểm cực trị là 0; 1; 2 và có đạo hàm liên tục trên R. Khi đó hàm số y = có bao nhiêu điểm cực trị?
5.
2.
3.
4.
Đồ thị hàm số y = có bao nhiêu điểm cực trị?
2.
3.
1.
0.
Với giá trị nào của tham số m thì hàm số y = đạt cực đại tại x = 1?
m 3
m = 3
m < 3
m > 3
Hàm số nào sau đây có đồ thị như hình bên?
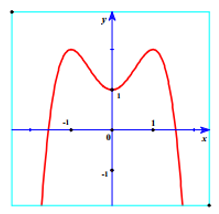
y =
y =
y =
y =








