30 câu hỏi
Số giao điểm của đồ thị hàm số y = +x+2 và đường thẳng y = -2x + 1 là:
3.
0.
2.
1.
Hàm số nào sau đây không có cực trị?
y =
y =
y =
y =
Tìm các giá trị của tham số m để hàm số đồng biến trên
m -1
m > -1
m
m > 1
Cho hàm số y = f(x) có đồ thị (C) và Mệnh đề nào sau đây đúng?
(C) không có tiệm cận ngang.
(C) có hai tiệm cận ngang là các đường thẳng x = 2 và x = -2.
(C) có đúng một tiệm cận ngang.
(C) có hai tiệm cận ngang là các đường thẳng y = 2 và y = -2.
Số tiệm cận của đồ thị hàm số y = là
3.
1.
0.
2.
Cho hàm số y = f(x). Đồ thị hàm số y = f'(x) như hình bên dưới. Hàm số g(x) = f3-x|| đồng biến trên khoảng nào trong các khoảng sau?
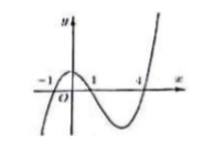
(4;7).
(2;3).
(-;-1)
(-1;2).
Giá trị nhỏ nhất của hàm số f(x) = trên đoạn [1;3] là
= 3
= 6
= 5
= 7
Bảng biến thiên dưới đây là của hàm số nào trong các hàm số sau?
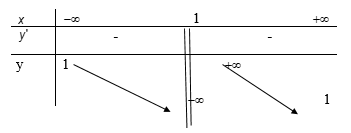
y =
y =
y =
y =
Tìm tất cả các nghiệm thực của tham số m sao cho đồ thị của hàm số y = có đúng một tiệm cận đứng.
m > 0 hoặc m < -4
m 0 hoặc m -4
m > 0 hoặc m -4
m
Gọi M là giá trị lớn nhất của hàm số y = xét trên đoạn [2;4], m0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng.
1 < < 5
-7 < < -5
-4 < < 0
< -8
Đồ thị của hàm số nào sau đây không có tiệm cận đứng
y =
y =
y =
y =
Cho hàm số y = . Khẳng định nào sau đây đúng?
Hàm số đạt cực đại tại x = 0 và cực tiểu tại y = -2.
Hàm số đạt cực tiểu tại x = 2 và cực đại tại y = 0.
Hàm số đạt cực đại tại x = -2 và cực tiểu tại y = 0.
Hàm số đạt cực đại tại x = 2 và cực tiểu tại y = 0.
Tìm tất cả các giá trị của tham số m để hàm số y = có giá trị lớn nhất trên nhỏ hơn hoặc bằng 1.
m 1
m 1
m -1
m -1
Hàm số nào trong các hàm số sau đây nghịch biến trên tập
y =
y =
y =
y = cot2x
Cho hàm số y = f(x) có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số f(x) trên đoạn [0;2] là:
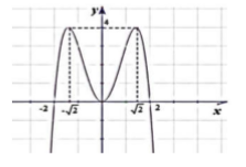
= 2
=
= 4
= 0
Cho f(x) có bảng biến thiên như sau:
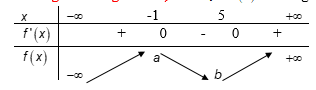
Hàm số nghịch biến trên khoảng nào dưới đây
(-1;5)
(-;1)
(-;5)
(1;+)
Cho hàm số y = . Khẳng định nào sau đây là đúng?
Hàm số chỉ có đúng một điểm cực trị.
Hàm số chỉ có đúng hai điểm cực trị.
Hàm số chỉ có đúng ba điểm cực trị.
Hàm số không có cực trị.
Giá trị của tham số m để hàm số y = có hai cực trị thỏa mãn là
1.
-1.
3.
-3.
Hàm số y = đồng biến trên khoảng nào sau đây?
Đường cong trong hình bên là đồ thị của một hàm số trong các hàm số ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
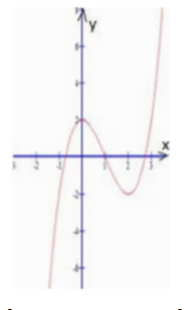
y =
y =
y =
y =
Cho hàm số y = có đồ thị như dưới đây. Tính giá trị biểu thức T = a + 2b + 3c
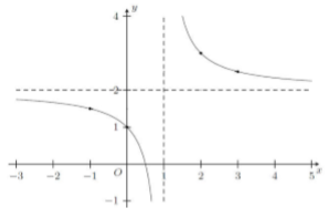
T = 1.
T = 2.
T = 3.
T = 4.
Cho hàm số f(x) liên tục trên và có đạo hàm f'(x) = (x+1). Hỏi hàm số f(x) có mấy điểm cực trị?
2.
3.
1.
5.
Hàm số nào sau đây đạt cực đại tại x = 1?
y = - x
y =
y =
y =
Cho hàm số y = f(x) có đồ thị như hình vẽ. Tìm tất cả các giá trị của tham số m để phương trình f(x) = m có ba nghiệm phân biệt.
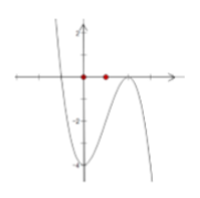
-4m 0
m > -4; m < 0
m > 0; m < -4
-4 < m < 0
Cho hàm số y = có đồ thị (C). Gọi M là điểm bất kì thuộc đồ thị (C). Tiếp tuyến của đồ thị (C) tại M cắt hai tiệm cận của đồ thị (C) tại P và Q. Giá trị nhỏ nhất của đoạn thẳng PQ bằng
3
4
2
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?
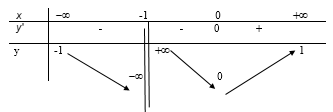
Đồ thị hàm số có 3 đường tiệm cận.
Đồ thị hàm số không có tiệm cận.
Hàm số có giá trị lớn nhất bằng 1 và có giá trị nhỏ nhất bằng 0.
Hàm số nghịch biến trên các khoảng (;0) và (0;)
Tìm tất cả các giá trị của tham số m để hàm số y = nghịch biến trên tập xác định.
Hàm số y = luôn đồng biến trên khoảng nào sau đây?
(2;+)
(0;+)
(0;4)
(-;0)
Tất cả các giá trị của m để phương trình có nghiệm thực là:
m
m
0 < m <
0 m
Tìm tất cả các giá trị m để phương trình có nghiệm là
m < -
- < m 1
- m <1
- < m <1








