22 câu hỏi
Trong không gian \[Oxyz\], cho \[\left( P \right):x + y - 2z + 5 = 0\] và \[\left( Q \right):4x + \left( {2 - m} \right)y + mz - 3 = 0\], \[m\] là tham số thực. Tìm tham số \[m\] sao cho mặt phẳng \[\left( Q \right)\] vuông góc với mặt phẳng \[\left( P \right)\].
\(m = - 3\).
\(m = - 2\).
\(m = 3\).
\(m = 2\).
Trong không gian \(Oxyz\) cho hai mặt phẳng \(\left( \alpha \right):x + 2y - z - 1 = 0\) và \(\left( \beta \right):2x + 4y - mz - 2 = 0.\) Tìm \(m\) để hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
\(m = 1\).
Không tồn tại \(m\).
\(m = - 2\).
\(m = 2\).
Trong không gian toạ độ \(Oxyz\), cho mặt phẳng \((P):x + 2y - 2z - 1 = 0\), mặt phẳng nào dưới đây song song với \(\left( P \right)\) và cách \(\left( P \right)\)một khoảng bằng \(3\).
\((Q):x + 2y - 2z + 8 = 0\).
\(\left( Q \right):x + 2y - 2z + 5 = 0\).
\((Q):x + 2y - 2z + 1 = 0\).
\[\left( Q \right):\,x + 2y - 2z + 2 = 0\].
Trong không gian với hệ tọa độ \[Oxyz\], cho mặt phẳng \(\left( P \right):2x + 2y - z - 1 = 0\). Mặt phẳng nào sau đây song song với \(\left( P \right)\) và cách \(\left( P \right)\) một khoảng bằng 3? Mệnh đề nào sau đây đúng và mệnh đề nào sai?
\(\left( Q \right):2x + 2y - z + 10 = 0\).
\(\left( Q \right):2x + 2y - z + 4 = 0\).
\(\left( Q \right):2x + 2y - z + 8 = 0\).
\(\left( Q \right):2x + 2y - z - 8 = 0\).
Trong không gian \(Oxyz\) cho \(A\left( {2;0;0} \right),B\left( {0;4;0} \right),C\left( {0;0;6} \right),D\left( {2;4;6} \right)\). Gọi \(\left( P \right)\) là mặt phẳng song song với \(mp\left( {ABC} \right)\), \(\left( P \right)\) cách đều \(D\) và mặt phẳng \(\left( {ABC} \right)\). Phương trình của \(\left( P \right)\) là
\(6x + 3y + 2z - 24 = 0\)
\(6x + 3y + 2z - 12 = 0\)
\(6x + 3y + 2z = 0\)
\(6x + 3y + 2z - 36 = 0\)
Trong không gian với hệ trục tọa độ \[Oxyz\], cho mặt phẳng \[\left( Q \right)\]: \[x + 2y + 2z - 3 = 0\], mặt phẳng \[\left( P \right)\] không qua \[O\], song song với mặt phẳng \[\left( Q \right)\]và \[d\left( {\left( P \right),\left( Q \right)} \right) = 1\]. Phương trình mặt phẳng \[\left( P \right)\] là
\[x + 2y + 2z + 1 = 0\]
\[x + 2y + 2z = 0\]
\[x + 2y + 2z - 6 = 0\]
\[x + 2y + 2z + 3 = 0\]
Trong không gian với hệ tọa độ \[Oxyz\], cho mặt phẳng \[\left( P \right):2x - 2y + z - 5 = 0\]. Viết phương trình mặt phẳng \[\left( Q \right)\] song song với mặt phẳng \[\left( P \right)\], cách \[\left( P \right)\] một khoảng bằng 3 và cắt trục \[Ox\] tại điểm có hoành độ dương.
\[\left( Q \right):2x - 2y + z + 4 = 0\].
\[\left( Q \right):2x - 2y + z - 14 = 0\].
\[\left( Q \right):2x - 2y + z - 19 = 0\].
\[\left( Q \right):2x - 2y + z - 8 = 0\].
Trong không gian \[Oxyz,\] cho 3 điểm \[A\left( {1;0;0} \right),{\rm{ }}B\left( {0; - 2;3} \right),C\left( {1;1;1} \right)\]. Gọi \[\left( P \right)\] là mặt phẳng chứa \[A,{\rm{ }}B\] sao cho khoảng cách từ \[C\] tới mặt phẳng \[\left( P \right)\] bằng \(\frac{2}{{\sqrt 3 }}\). Phương trình mặt phẳng \[\left( P \right)\] là
\[\left[ {\begin{array}{*{20}{c}}{2x + 3y + z - 1 = 0}\\{3x + y + 7z + 6 = 0}\end{array}} \right.\]
\[\left[ {\begin{array}{*{20}{c}}{x + 2y + z - 1 = 0}\\{ - 2x + 3y + 6z + 13 = 0}\end{array}} \right.\]
\[\left[ {\begin{array}{*{20}{c}}{x + y + 2z - 1 = 0}\\{ - 2x + 3y + 7z + 23 = 0}\end{array}} \right.\]
\[\left[ {\begin{array}{*{20}{c}}{x + y + z - 1 = 0}\\{ - 23x + 37y + 17z + 23 = 0}\end{array}} \right.\]
Trong hệ trục tọa độ \(Oxyz\) cho \(3\) điểm \(M\left( {4;2;1} \right),N\left( {0;0;3} \right),Q\left( {2;0;1} \right)\). Viết phương trình mặt phẳng chứa \(OQ\) và cách đều \(2\) điểm \(M,N\).
\(x - 2y - 2z = 0\) hoặc \(x + 4y - 2z = 0\).
\(x + 2y + 2z = 0\) hoặc \(x - 4y - 2z = 0\).
\(x + 2y - 2z = 0\) hoặc \(x + 4y - 2z = 0\).
\(x + 2y - 2z = 0\) hoặc \(x - 4y - 2z = 0\).
Cho tứ diện \[OABC\], có \[OA,OB,OC\]đôi một vuông góc và \[OA = 5,OB = 2,OC = 4\]. Gọi \[M,N\] lần lượt là trung điểm của \[OB\]và \[OC\]. Gọi \[G\] là trọng tâm của tam giác \[ABC\]. Khoảng cách từ \[G\] đến mặt phẳng \[\left( {AMN} \right)\] là:
\[\frac{{20}}{{3\sqrt {129} }}.\]
\[\frac{{20}}{{\sqrt {129} }}.\]
\[\frac{1}{4}.\]
\[\frac{1}{2}.\]
Cho hình chóp \[S.ABCD\] đáy là hình thang vuông tại \[A\] và \(D\), \[SA \bot \left( {ABCD} \right)\]. Góc giữa \(SB\) và mặt phẳng đáy bằng \({45^{\rm{o}}}\), \(E\) là trung điểm của \[SD\], \(AB = 2a\), \(AD = DC = a\). Tính khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {ACE} \right)\).
\(\frac{{2a}}{3}\).
\(\frac{{4a}}{3}\).
\(a\).
\(\frac{{3a}}{4}\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình chữ nhật. Biết \(A\left( {0;0;0} \right)\),\(D\left( {2;0;0} \right)\),\(B\left( {0;4;0} \right)\),\(S\left( {0;0;4} \right)\). Gọi \(M\) là trung điểm của \(SB\). Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( {CDM} \right)\).
\(d\left( {B,\left( {CDM} \right)} \right) = 2\).
\(d\left( {B,\left( {CDM} \right)} \right) = 2\sqrt 2 \).
\(d\left( {B,\left( {CDM} \right)} \right) = \frac{1}{{\sqrt 2 }}\).
\(d\left( {B,\left( {CDM} \right)} \right) = \sqrt 2 \).
Một phần sân trường được định vị bởi các điểm \(A,B,C,D\), như hình vẽ.
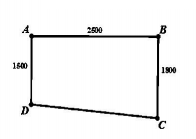
Bước đầu chúng được lấy “ thăng bằng” để có cùng độ cao, biết \(ABCD\) là hình thang vuông ở \(A\) và \(B\) với độ dài \(AB = 25\,{\rm{m}}\), \(AD = 15\,{\rm{m}}\), \(BC = 18\,{\rm{m}}\). Do yêu cầu kĩ thuật, khi lát phẳng phần sân trường phải thoát nước về góc sân ở \(C\) nên người ta lấy độ cao ở các điểm \(B\), \(C\), \(D\) xuống thấp hơn so với độ cao ở \(A\) là \(10\,{\rm{cm}}\), \(a\,{\rm{cm}}\), \(6\,{\rm{cm}}\)tương ứng. Giá trị của \(a\) là số nào sau đây?
\(15,7\,{\rm{cm}}\).
\(17,2\,{\rm{cm}}\).
\[18,1\,{\rm{cm}}\].
\(17,5\,{\rm{cm}}\).
Trong không gian Oyz cho điểm . Viết phương trình mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox,Oy,Oz lần lượt tại A,B,C sao cho M là trọng tâm của tam giác ABC.
Trong không gian với hệ trục tọa độ Oyz cho điểm Mặt phẳng nào sau đây cắt các trục Ox,Oy,Oz lần lượt tại A,B,C sao cho G là trọng tâm tứ diện OABC
Viết phương trình mặt phẳng () đi qua , biết() cắt trục Ox,Oy,Oz lần lượt tại A,B,C sao cho tam giác ABC nhận M làm trực tâm
Trong không gian với hệ trục toạ độ \[Oxyz,\]điểm \(M\left( {a,b,c} \right)\) thuộc mặt phẳng \(\left( P \right):x + y + z - 6 = 0\) và cách đều các điểm \(A\left( {1;6;0} \right),B\left( { - 2;2; - 1} \right),C\left( {5; - 1;3} \right).\) Tích \(abc\) bằng
\(6\)
\( - 6\)
\(0\)
\(5\)
Trong không gian với hệ tọa độ \(Oxyz,\)cho điểm \(M\left( {3;2;1} \right)\). Mặt phẳng \(\left( P \right)\) đi qua \(M\) và cắt các trục tọa độ \(Ox\), \(Oy\), \(Oz\) lần lượt tại các điểm \(A\), \(B\), \(C\) không trùng với gốc tọa độ sao cho \(M\) là trực tâm tam giác \(ABC\). Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng \(\left( P \right)\).
\(3x + 2y + z + 14 = 0\).
\(2x + y + 3z + 9 = 0\).
\(3x + 2y + z - 14 = 0\).
\(2x + y + z - 9 = 0\).
Trong không gian với hệ tọa độ Oyz, cho các điểm , . Mặt phẳng (P) đi qua A, trực tâm H của tam giác ABC và vuông góc với mặt phẳng (ABC) có phương trình là
.
.
.
Trong không gian với hệ tọa độ Oyz, viết phương trình mặt phẳng (P) đi qua A(1;1;1) và B(0;2;2) đồng thời cắt các tia Ox, Oy lần lượt tại hai điểm M,N ( không trùng với gốc tọa độ O) sao cho OM=2ON
Trong không gian Oyz, cho mặt phẳng () đi qua điểm và cắt các trục Ox,Oy,Oz lần lượt tại A,B,C (khác gốc tọa độ O) sao cho M là trực tâm tam giác ABC. Mặt phẳng ()có phương trình dạng. Tính tổng .
8.
14.
6.
11.
Trong không gian tọa độ Oyz, cho mặt phẳng ( đi qua và chắn trên Oz một đoạn dài gấp đôi các đoạn chắn trên các tia Ox, Oy. Giả sử (a,c,d là các số nguyên). Tính .
3.
-3.
.
.
