30 CÂU HỎI
Trong không gian \(Oxyz\), cho ba điểm , và . Mặt phẳng có phương trình là:
.
.C. .
.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm . Khi đó, phương trình mặt phẳng (ABC) là . Hãy xác định a và d.
.
.
.
.
Trong không gian \[Oxyz\], cho điểm \(A\left( {0;\, - 3;\,2} \right)\) và mặt phẳng \(\left( P \right):\,2x - y + 3z + 5 = 0\). Mặt phẳng đi qua \(A\) và song song với \(\left( P \right)\) có phương trình là:
\(2x - y + 3z + 9 = 0\).
\(2x + y + 3z - 3 = 0\).
\(2x + y + 3z + 3 = 0\).
\(2x - y + 3z - 9 = 0\).
Trong không gian \(Oxyz\), cho hai điểm và . Mặt phẳng đi qua \(A\) và vuông góc với \(AB\) có phương trình là
\(x + 2y + 2z - 11 = 0\).
\(x + 2y + 4z - 17 = 0\).
Trong mặt phẳng \(Oxyz\), cho hai điểm \(A\left( {1;0;0} \right)\) và \(B\left( {3;2;1} \right)\). Mặt phẳng đi qua \(A\) và vuông góc với \(AB\)có phương trình là:
\(2x + 2y + z - 2 = 0\).
\(4x + 2y + z - 17 = 0\).
\(4x + 2y + z - 4 = 0\).
\(2x + 2y + z - 11 = 0\).
Trong không gian với hệ tọa độ Oxyz, cho hai điểm ) và . Viết phương trình của mặt phẳng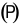 
đi qua A và vuông góc với đường thẳng AB.
Trong không gian Oxyz, cho ba điểm A(1;-1;1), B(2;1;0),C(1;-1;2). Mặt phẳng đi qua A và vuông góc với đường thẳng BC có phương trình là
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(0;1;2),, B(2;-2;1),, C(-2;0;1). Phương trình mặt phẳng đi qua A và vuông góc với BC là
.
.
.
.
Trong không gian Oxyz, mặt phẳng (P) đi qua hai điểm A(0;1;0),B(2;3;1) và vuông góc với mặt phẳng có phương trình là
.
.
.
Cho hai mặt phẳng . Phương trình mặt phẳng đi qua gốc tọa độ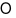 
đồng thời vuông góc với cả và là:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;1),B(-1;1;3) và mặt phẳng (P):x-3y+2z-5=0 . Một mặt phẳng (Q) đi qua hai điểm A,B và vuông góc với mặt phẳng (P) có dạng ax+by+cz-11=0 . Khẳng định nào sau đây là đúng?
Trong không gian Oxyz cho hai mặt phẳng (P):x-3y+2z-1=0, (Q):x-z+2=0 . Mặt phẳng () vuông góc với cả (P) và (Q) đồng thời cắt trục Ox tại điểm có hoành độ bằng 3 Phương trình của mp () là
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P):ax+by+cz-9=0chứa hai điểm A(3;2;1), B(-3;5;2)và vuông góc với mặt phẳng (Q):3x+y+z+4=0 Tính tổng S=a+b+c
S=-12
S=2.
S=4.
S=-2.
Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm B(2;1;-3), đồng thời vuông góc với hai mặt phẳng (Q):x+y+3z=0 ,(R):2x-y+z=0 là
4x+5y-3z+22=0.
4x-5y-3z-12=0
2x+y-3z-14=0
4x+5y-3z-22=0
Khoảng cách từ điểm \[M\left( {3;\,\,2;\,\,1} \right)\] đến mặt phẳng (P): \(Ax + Cz + D = 0\), \(A.C.D \ne 0\). Chọn khẳng định đúng trong các khẳng định sau:
\(d(M,(P)) = \frac{{\left| {3A + C + D} \right|}}{{\sqrt {{A^2} + {C^2}} }}\)
\[d(M,(P)) = \frac{{\left| {A + 2B + 3C + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}.\]
\(d(M,(P)) = \frac{{\left| {3A + C} \right|}}{{\sqrt {{A^2} + {C^2}} }}.\)
\[d(M,(P)) = \frac{{\left| {3A + C + D} \right|}}{{\sqrt {{3^2} + {1^2}} }}.\]
Trong không gian với hệ tọa độ , cho mặt phẳng \(P\) có phương trình: và điểm . Tính khoảng cách từ đến \(P\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):2x - 2y + z - 1 = 0\). Khoảng cách từ điểm \(M\left( { - 1;2;0} \right)\) đến mặt phẳng \(\left( P \right)\) bằng
\(5\).
\(2\).
\(\frac{5}{3}\).
\[\frac{4}{3}\].
Trong không gian \[Oxyz\], tính khoảng cách từ \[M\left( {1;2; - 3} \right)\] đến mặt phẳng \[\left( P \right):\,x + 2y + 2{\rm{z}} - 10 = 0\].
\[\frac{{11}}{3}\].
\[3\].
\[\frac{7}{3}\].
\[\frac{4}{3}\].
Trong không gian \[Oxyz\], cho mặt phẳng \(\left( P \right):2x - y + 2z - 4 = 0\). Gọi \(H\) là hình chiếu vuông góc của điểm \(M\left( {3\,;\,1\,;\, - 2} \right)\) lên mặt phẳng \(\left( P \right)\). Độ dài đoạn thẳng \(MH\) là
\(2\).
\(\frac{1}{3}\).
\(1\).
\(3\).
Trong không gian với hệ trục tọa độ \(Oxyz\), gọi \(H\) là hình chiếu vuông góc của điểm \[A\left( {1; - 2;3} \right)\] lên mặt phẳng \(\left( P \right):2x - y - 2z + 5 = 0\). Độ dài đoạn thẳng \(AH\) là
\(3\).
\(7\)
.C. \(4\).
\(1\).
Khoảng cách từ điểm \(M\left( { - 4; - 5;6} \right)\) đến mặt phẳng (Oxy), (Oyz) lần lượt bằng:
6 và 4.
6 và 5.
5 và 4.
4 và 6.
Tính khoảng cách từ điểm \[B\left( {{x_0};{y_0};{z_0}} \right)\]đến mặt phẳng (P): y + 1 = 0. Chọn khẳng định đúng trong các khẳng định sau:
\({y_0}.\)
\(\left| {{y_0}} \right|.\)
\(\frac{{\left| {{y_0} + 1} \right|}}{{\sqrt 2 }}.\)
\(\left| {{y_0} + 1} \right|.\)
Khoảng cách từ điểm \(C\left( { - 2;\,\,0;\,\,0} \right)\) đến mặt phẳng (Oxy) bằng:
0.
2.
1.
\(\sqrt 2 .\)
Trong không gian \(Oxyz\), Khoảng cách giữa hai mặt phẳng \(\left( P \right):x + 2y + 2z - 10 = 0\) và \(\left( Q \right):x + 2y + 2z - 3 = 0\)bằng:
\(\frac{4}{3}\)
\(\frac{8}{3}\).
\(\frac{7}{3}\).
\(3\).
Trong không gian \(Oxyz\), khoảng cách giữa hai mặt phẳng \(\left( P \right):x + 2y + 3z - 1 = 0\) và \(\left( Q \right):x + 2y + 3z + 6 = 0\) là
\[\frac{7}{{\sqrt {14} }}\]
\(\frac{8}{{\sqrt {14} }}\)
\(14\)
\(\frac{5}{{\sqrt {14} }}\)
Trong không gian \[Oxyz\], khoảng cách giữa hai mặt phẳng \[\left( P \right):x + 2y + 2z - 8 = 0\] và \[\left( Q \right):x + 2y + 2z - 4 = 0\] bằng
1.
\[\frac{4}{3}\].
2.
\[\frac{7}{3}\].
Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right):2x + y + z - 2 = 0\) vuông góc với mặt phẳng nào dưới đây?
\(2x - y - z - 2 = 0\).
\(x - y - z - 2 = 0\).
\(x + y + z - 2 = 0\).
\(2x + y + z - 2 = 0\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hai mặt phẳng \(\left( P \right):2x + my + 3z - 5 = 0\) và\(\left( Q \right):nx - 8y - 6z + 2 = 0\), với \(m,n \in \mathbb{R}\). Xác định \(m,n\) để \(\left( P \right)\)song song với \(\left( Q \right)\).
\(m = n = - \;4\).
\(m = 4;n = - \;4\).
\(m = - \;4;n = 4\).
\(m = n = 4\).
Trong không gian \[Oxyz,\] cho hai mặt phẳng \[\left( P \right):x--{\rm{2}}y + {\rm{2}}z--{\rm{3}} = 0\] và \[\left( Q \right):mx + y--{\rm{2}}z + {\rm{1}} = 0\]. Với giá trị nào của m thì hai mặt phẳng đó vuông góc với nhau?
\(m = 1\)
\(m = - 1\)
\(m = - 6\)
\(m = 6\)
Trong không gian \[Oxyz\], cho mặt phẳng ba mặt phẳng \(\left( P \right):x + y + z - 1 = 0\), \(\left( Q \right):2x + my + 2z + 3 = 0\) và \(\left( R \right): - x + 2y + nz = 0\). Tính tổng \(m + 2n\), biết rằng \(\left( P \right) \bot \left( R \right)\) và \(\left( P \right)//\left( Q \right)\)
\( - 6\).
1.
0.
6.