8 câu hỏi
Cho hàm số y = 2x2 – 4x + 3 có đồ thị là parabol (P). Mệnh đề nào sau đây sai?
(P) không có giao điểm với trục hoành;
(P) có đỉnh là S(1; 1);
(P) có trục đối xứng là đường thẳng y = 1;
(P) đi qua điểm M(–1; 9).
Cho hàm số y = –x2 – x – 1. Tập giá trị của hàm số đã cho là:
\(T = \left( { - \infty ;\frac{3}{4}} \right]\);
\(T = \left( { - \infty ; - \frac{3}{4}} \right]\);
\(T = \left[ { - \frac{3}{4}; + \infty } \right)\);
\(T = \left( { - \infty ; - \frac{3}{4}} \right)\).
Đồ thị dưới đây là của hàm số nào sau đây?
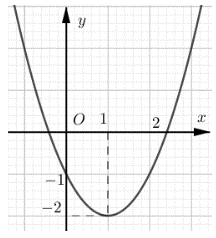
y = –x2 – 2x + 3;
y = x2 + 2x – 2;
y = 2x2 – 4x – 2;
y = x2 – 2x – 1.
Điều kiện của m để hàm số y = (m – 1)x2 + 2mx – m2 + 4 là hàm số bậc hai là:
m > 1;
m < 1;
m ≠ 1;
m ≥ 1.
Parabol (P): y = ax2 + 3x – 2 (a ≠ 0)có trục đối xứng là đường thẳng x = –3 là:
y = x2 + 3x – 2;
\(y = \frac{1}{2}{x^2} + x - 2\);
\(y = \frac{1}{2}{x^2} - 3x - 2\);
\(y = \frac{1}{2}{x^2} + 3x - 2\).
Cho hàm số f(x) = x2 – 4x + 5. Khẳng định nào sau đây đúng?
Hàm số nghịch biến trên (–∞; 2) và đồng biến trên (2; +∞);
Hàm số nghịch biến trên (–∞; 2) và (2; +∞);
Hàm số đồng biến trên (–∞; 2) và nghịch biến trên (2; +∞);
Hàm số đồng biến trên (–∞; 2) và (2; +∞).
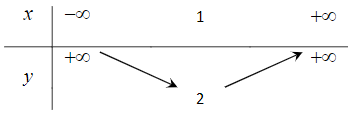
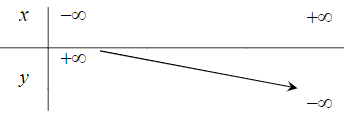
Bảng biến thiên nào dưới đây là của hàm số y = –x2 + 2x + 1?
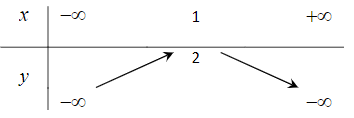
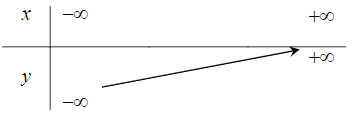
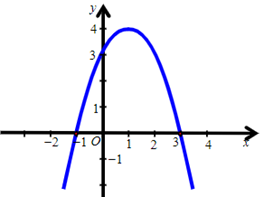
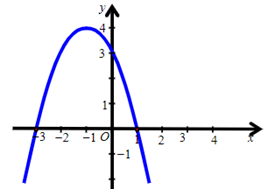
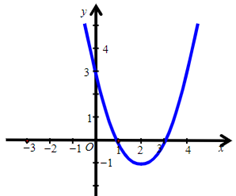
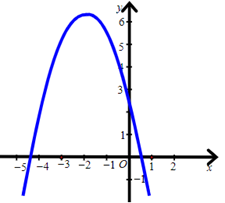
Hàm số y = –x2 + 2x + 3 có đồ thị là hình nào trong các hình sau?