11 câu hỏi
Phần I: Trắc nghiệm nhiều phương án lựa chọn
Cho hàm số \[y = - {x^2} + 4x + 1\]. Khẳng định nào sau đây sai?
Trên khoảng \[\left( { - \infty ;1} \right)\], hàm số đồng biến.
Hàm số nghịch biến trên khoảng \[\left( {2; + \infty } \right)\] và đồng biến trên khoảng \[\left( { - \infty ;2} \right)\].
Trên khoảng \[\left( {3; + \infty } \right)\], hàm số nghịch biến.
Hàm số nghịch biến trên khoảng \[\left( {4; + \infty } \right)\] và đồng biến trên khoảng \[\left( { - \infty ;4} \right)\].
Hàm số \(f\left( x \right) = {x^2} - 2x + 3\) đồng biến trên khoảng nào dưới đây?
\(\left( {1; + \infty } \right)\).
\(\left( { - 2; + \infty } \right)\).
\(\left( { - \infty ;1} \right)\).
\(\left( { - 3; + \infty } \right)\).
Cho parabol \(\left( P \right):y = 3{x^2} - 2x + 1\). Điểm nào sau đây là đỉnh của \(\left( P \right)\)?
\(I\left( {0;1} \right)\).
\(I\left( {\frac{1}{3};\,\frac{2}{3}} \right)\).
\(I\left( { - \frac{1}{3};\,\frac{2}{3}} \right)\).
\(I\left( {\frac{1}{3};\, - \frac{2}{3}} \right)\).
Đồ thị nào sau đây là đồ thị của hàm số \[y = {x^2} - 2x - 3\]?
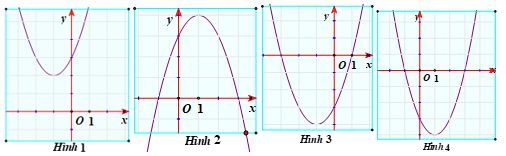
Hình \[1\].
Hình \[2\].
Hình \[3\].
Hình \[4\].
Xác định các hệ số \(a\) và \(b\) để parabol \(\left( P \right):y = a{x^2} + 4x - b\) có đỉnh \(I\left( { - 1; - 5} \right)\).
\(\left\{ \begin{array}{l}a = 3\\b = - 2\end{array} \right..\)
\(\left\{ \begin{array}{l}a = 3\\b = 2\end{array} \right..\)
\(\left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right..\)
\(\left\{ \begin{array}{l}a = 2\\b = - 3\end{array} \right..\)
Cho hàm số \[y = a{x^2} + bx + c\] có đồ thị như hình bên.
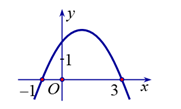
Khẳng định nào sau đây đúng?
\[a > 0\], \[b > 0\], \[c > 0\].
\[a > 0\], \[b < 0\], \[c < 0\].
\[a < 0\], \[b < 0\], \[c > 0\].
\[a < 0\], \[b > 0\], \[c > 0\].
Tọa độ giao điểm của \(\left( P \right)\,:\,y = {x^2} - 4x\) với đường thẳng \(d\,:\,y = - x - 2\) là
\(M\left( {0;\, - 2} \right)\), \(N\left( {2;\, - 4} \right)\).
\(M\left( { - 1;\, - 1} \right)\), \(N\left( { - 2;\,0} \right)\).
\(M\left( {\, - 3;\,1} \right)\), \(N\left( {3;\, - 5} \right)\).
\(M\left( {1;\, - 3} \right)\), \(N\left( {2;\, - 4} \right)\).
Khẳng định nào dưới đây đúng?
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị lớn nhất bằng \(\frac{{25}}{{12}}\).
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị nhỏ nhất bằng \(\frac{{25}}{{12}}\).
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị lớn nhất bằng \(\frac{{25}}{3}\).
Hàm số \(y = - 3{x^2} + x + 2\) có giá trị nhỏ nhất bằng \(\frac{{25}}{3}\).
Tìm giá trị thực của tham số \(m \ne 0\) để hàm số \(y = m{x^2} - 2mx - 3m - 2\) có giá trị nhỏ nhất bằng \( - 10\) trên \(\mathbb{R}.\)
\(m = 1.\)
\(m = 2.\)
\(m = - 2.\)
\(m = - 1.\)
Gọi \(S\) là tập hợp tất cả các giá trị dương của tham số \(m\) để giá trị nhỏ nhất của hàm số \(y = f\left( x \right) = 4{x^2} - 4mx + {m^2} - 2m\) trên đoạn \(\left[ { - 2;\,0} \right]\) bằng \(3\). Tổng \(T\) các phần tử của \(S\) là
\(T = 3\).
\(T = \frac{1}{2}\).
\(T = \frac{9}{2}\).
\(T = - \frac{3}{2}\).
Parabol\(y = a{x^2} + bx + c\) đi qua ba điểm \(A\left( {0; - 1} \right)\), \(B\left( {1; - 1} \right)\), \(C\left( { - 1;1} \right)\)có phương trình là
\(y = {x^2} - x + 1\).
\(y = {x^2} - x - 1\).
\(y = {x^2} + x - 1\).
\(y = {x^2} + x + 1\).
