14 câu hỏi
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên. Khẳng định nào sau đây đúng?
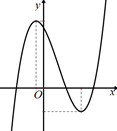
\(a > 0,b < 0,c < 0,d > 0\).
\(a < 0,b > 0,c < 0,d > 0\).
\(a > 0,b < 0,c > 0,d > 0\).
\(a > 0,b > 0,c < 0,d > 0\).
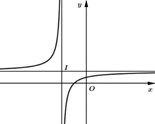
Cho hàm số \(y = \frac{{bx - c}}{{x - a}}\) (\(a \ne 0\) và \(a\), \(b\), \(c \in \mathbb{R}\)) có đồ thị như hình bên. Khẳng định nào dưới đây đúng?
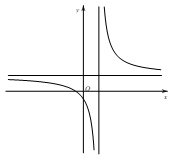
\(a > 0\), \(b < 0\), \(c - ab < 0\).
\(a > 0\), \(b > 0\), \(c - ab < 0\).
\(a < 0\), \(b > 0\), \(c - ab < 0\).
\(a < 0\), \(b < 0\), \(c - ab > 0\).
Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\] có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
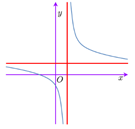
\[ab < 0\], \[cd < 0\].
\[bc > 0\], \[ad < 0\].
\[ac > 0\], \[bd > 0\].
\[bd < 0\], \[ad > 0\].
Giá trị của \(a\), \(b\) để hàm số \(y = \frac{{ax + b}}{{x - 1}}\) có đồ thị như hình vẽ là
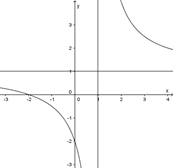
\(a = 1\), \(b = - 2\).
\(a = 1\), \(b = 2\).
\(a = - 1\), \(b = - 2\).
\(a = - 1\), \(b = 2\).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ
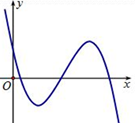 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
\[a < 0,b > 0,c < 0,d > 0\].
\[a > 0,b > 0,c < 0,d > 0\].
\[a < 0,b < 0,c < 0,d > 0\].
\[a < 0,b > 0,c > 0,d > 0\].
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong trong hình dưới đây. Mệnh đề nào sau đây đúng?
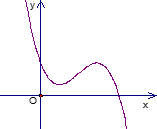
\(a > 0\), \(c > 0\), \(d > 0\).
\(a < 0\), \(c > 0\), \(d > 0\).
\(a < 0\), \(c < 0\), \(d < 0\).
\(a < 0\), \(c < 0\), \(d > 0\).
Cho hàm số \(y = \frac{{ax - b}}{{x - 1}}\) có đồ thị như hình dưới.
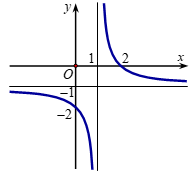
Khẳng định nào dưới đây là đúng?
\(b < 0 < a\).
\(0 < b < a\).
\(b < a < 0\).
\(0 < a < b\).
Cho hàm số\(y = \frac{{ax + 1}}{{x - b}}\) có đồ thị như hình vẽ bên.
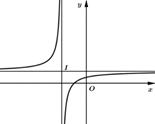
Mệnh đề nào sau đây đúng?
\(a > 0 > b\).
\(a > b > 0\).
\(a < b < 0\).
\(a < 0 < b\).
Hàm số \[y = a{x^3} + b{x^2} + cx + d\,,\,\,\,\left( {a \ne 0} \right)\] có đồ thị sau.
Mệnh đề nào sau đây đúng?
\[a > 0;\,\,b > 0;\,\,c > 0;\,\,d{\rm{ }} > {\rm{ }}0\].
\[a > 0;\,\,b < 0;\,\,c = 0;\,\,d{\rm{ }} > {\rm{ }}0\].
\[a > 0;\,\,b > 0;\,\,c = 0;\,\,d{\rm{ }} > {\rm{ }}0\].
\[a > 0;\,\,b < 0;\,\,c > 0;\,\,d{\rm{ }} > {\rm{ }}0\].
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong như hình vẽ bên. Mệnh đề nào dưới đây đúng?
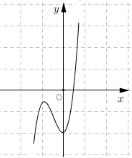
\(a > 0,\,b < 0,\,c = 0,\,d < 0\).
\(a > 0,\,b = 0,\,c < 0,\,d < 0\).
\(a > 0,\,b = 0,\,c > 0,\,d < 0\).
\(a > 0,\,b > 0,\,c = 0,\,d < 0\).
Cho hàm số \[f\left( x \right) = a{x^3} + b{x^2} + cx + d\] \[\left( {a,\,\,b,\,\,c,\,\,d \in \mathbb{R},\,\,a \ne 0} \right)\] có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
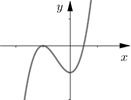
\(a > 0\), \(b > 0\), \(c > 0\) \(d < 0\).
\(a < 0\), \(b < 0\), \(c = 0\), \(d < 0\).
\(a > 0\), \(b > 0\), \(c = 0\), \(d < 0\).
\(a > 0\), \(b < 0\), \(c = 0\), \(d < 0\).
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ ở bên. Mệnh đề nào sau đây đúng?
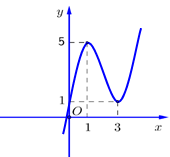
\(a > 0\), \(b > 0\), \(c < 0\), \(d > 0\).
\(a > 0\), \(b > 0\), \(c > 0\), \(d > 0\).
\(a > 0\), \(b < 0\), \(c > 0\), \(d > 0\).
\(a < 0\), \(b < 0\), \(c > 0\), \(d < 0\).
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\)có đồ thị là đường cong như hình vẽ.
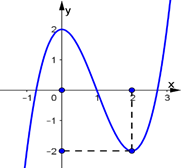
Tính tổng \(S = a + b + c + d\).
\(S = 0\).
\(S = 6\).
\(S = - 4\).
\(S = 2\).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên.
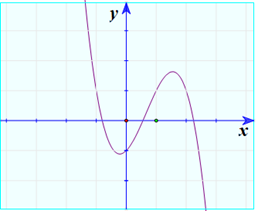
Mệnh đề nào dưới đây đúng?
\[a < 0,b < 0,c > 0,d < 0\].
\[a < 0,b > 0,c > 0,d < 0\].
\[a < 0,b < 0,c < 0,d < 0\].
\[a < 0,b > 0,c < 0,d < 0\].
