30 câu hỏi
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
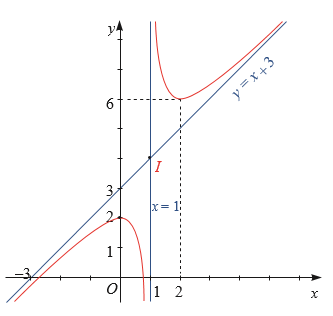
\[y = \frac{{x + 3}}{{x - 2}}\].
\[y = {x^3} - 3{x^2} - 2\].
\[y = \frac{{{x^2} + 2x - 4}}{{x - 2}}\].
\[y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\].
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
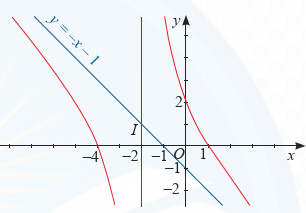
\[y = {x^3} + 3{x^2} - 1\].
\[y = \frac{{ - {x^2} - 3x + 4}}{{x + 2}}\].
\[y = \frac{{x + 3}}{{x + 2}}\].
\[y = \frac{{{x^2} - 3x + 4}}{{x - 2}}\].
Câu 1. Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
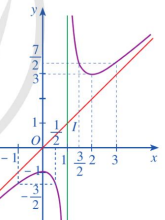
\[y = \frac{{x + 1}}{{x - 1}}\].
\[y = \frac{{{x^2} - x + 1}}{{x + 1}}\].
\[y = - {x^3} + 3{x^2} - 1\].
\[y = \frac{{{x^2} - x + 1}}{{x - 1}}\].
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
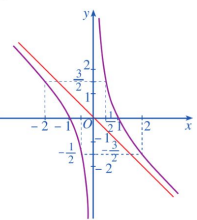
\[y = \frac{1}{x}\].
\[y = \frac{{x + 1}}{{x - 1}}\].
\[y = \frac{{ - {x^2} + 1}}{{x - 2}}\].
\[y = \frac{{ - {x^2} + 1}}{x}\].
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
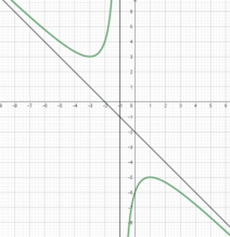
\[y = {x^3} + 3{x^2} - 1\].
\[y = {x^3} - 3{x^2} - 2\].
\[y = - {x^3} + 3{x^2} - 1\].
\[y = \frac{{ - {x^2} - 3x - 6}}{{x + 1}}\].
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
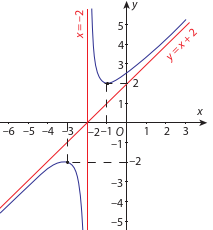
\[y = \frac{{{x^2} + 4x + 5}}{{x + 2}}\].
\[y = \frac{{4x + 5}}{{x + 2}}\].
\[y = - {x^3} + 3{x^2} - 1\]
\[y = \frac{{{x^2} + 4x + 4}}{{x + 1}}\].
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
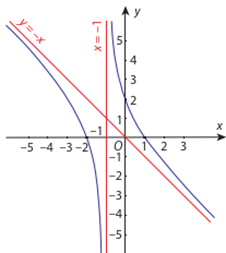
\[y = \frac{{ - x + 2}}{{x + 1}}\].
\[y = \frac{{ - {x^2} - x + 2}}{{x + 1}}\].
\[y = - {x^3} + 3{x^2} - 1\].
\[y = \frac{{{x^2} - x + 2}}{{x + 1}}\].
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
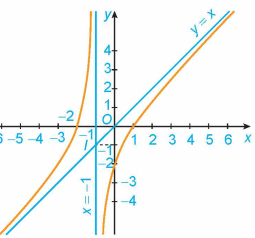
\[y = {x^3} + 3{x^2} - 1\].
\[y = \frac{{ - {x^2} + x - 2}}{{x + 1}}\].
\[y = \frac{{x - 2}}{{x + 1}}\].
\[y = \frac{{{x^2} + x - 2}}{{x + 1}}\].
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
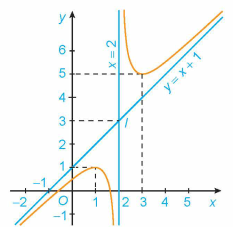
\[y = \frac{{{x^2} - x - 1}}{{x - 2}}\].
\[y = \frac{{{x^2} + x + 1}}{{x - 2}}\].
\[y = \frac{{ - x + 1}}{{x - 2}}\].
\[y = \frac{{ - x - 1}}{{x - 2}}\].
Bảng biến thiên trong hình vẽ dưới đây là của hàm số nào trong các đáp án sau?

\[y = \frac{{{x^2} - x + 1}}{{x - 1}}\].
\[y = \frac{{{x^2} - 2x + 5}}{{x + 1}}\].
\[y = \frac{{ - {x^2} + 2x - 5}}{{x - 1}}\].
\[y = \frac{{{x^2} - 2x + 5}}{{x - 1}}\].
Bảng biến thiên trong hình vẽ dưới đây là của hàm số nào trong các đáp án sau?
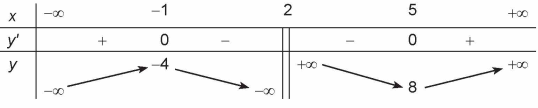
\[y = \frac{{ - {x^2} + 2x - 5}}{{x - 2}}\].
\[y = \frac{{{x^2} - 2x + 9}}{{x - 2}}\].
\[y = \frac{{{x^2} - 2x + 3}}{{x + 1}}\].
\[y = \frac{{{x^2} - 2x + 1}}{{x - 2}}\].
Bảng biến thiên trong hình vẽ dưới đây là của hàm số nào trong các đáp án sau?
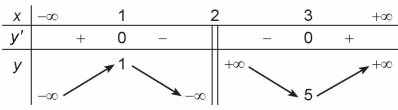
\[y = \frac{{ - {x^2} + 2x - 5}}{{x - 2}}\].
\[y = \frac{{{x^2} - 2x + 1}}{{x - 2}}\].
\[y = \frac{{{x^2} - 2x + 9}}{{x - 2}}\].
\[y = \frac{{{x^2} - x - 1}}{{x - 2}}\].
Bảng biến thiên trong hình vẽ dưới đây là của hàm số nào trong các đáp án sau?
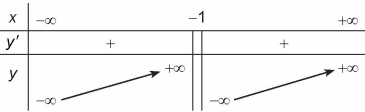
\[y = \frac{{{x^2} - x - 1}}{{x + 2}}\].
\[y = \frac{{{x^2} - x - 1}}{{x - 2}}\].
\[y = \frac{{{x^2} + x - 2}}{{x + 1}}\].
\[y = \frac{{{x^2} + x - 2}}{{x - 1}}\]
Bảng biến thiên trong hình vẽ dưới đây là của hàm số nào trong các đáp án sau?

\[y = x + 1 + \frac{1}{x}\].
\[y = \frac{{4x + 5}}{x}\].
\[y = \frac{{{x^2} + 4x + 5}}{x}\].
\[y = x + \frac{1}{x}\].
Bảng biến thiên trong hình vẽ dưới đây là của hàm số nào trong các đáp án sau?

\[y = \frac{{{x^2} + 4x + 5}}{{x + 2}}\].
\[y = \frac{{{x^2} + x + 1}}{{x + 1}}\].
\[y = \frac{{ - {x^2} - x + 2}}{{x + 1}}\].
\[y = \frac{{{x^2} + 4x + 5}}{{x - 2}}\].
Bảng biến thiên trong hình vẽ dưới đây là của hàm số nào trong các đáp án sau?
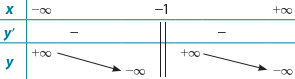
\[y = \frac{{ - {x^2} - x + 2}}{{x - 1}}\].
\[y = \frac{{{x^2} + x + 1}}{{x + 1}}\].
\[y = \frac{{{x^2} - x - 1}}{{x + 2}}\].
\[y = \frac{{ - {x^2} - x + 2}}{{x + 1}}\].
Bảng biến thiên trong hình vẽ dưới đây là của hàm số nào trong các đáp án sau?
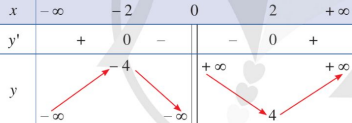
\[y = \frac{{{x^2} - x + 4}}{x}\].
\[y = \frac{{{x^2} + 1}}{x}\].
\[y = \frac{{{x^2} + x + 1}}{{x + 1}}\].
\[y = \frac{{{x^2} + 4}}{x}\].
Bảng biến thiên trong hình vẽ dưới đây là của hàm số nào trong các đáp án sau?
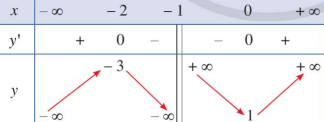
\[y = \frac{{{x^2} - x + 4}}{{x + 1}}\].
\[y = \frac{{{x^2} + 4}}{x}\].
\[y = \frac{{{x^2} + 4}}{{x + 1}}\].
\[y = \frac{{{x^2} + x + 1}}{{x + 1}}\].
Xác định \(a\), \(b\), \(c\) để hàm số \(y = \frac{{ax - 1}}{{bx + c}}\) có đồ thị như hình vẽ bên. Chọn đáp án đúng?
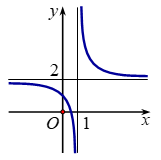
\(a = 2,\,\,b = 1,\,c = - 1.\)
\(a = 2,\,\,b = 1,\,c = 1.\)
\(a = 2,\,\,b = 2,\,c = - 1.\)
\(a = 2,\,\,b = - 1,\,c = 1.\)
Đường cong ở hình bên là đồ thị hàm số \(y = \frac{{ax + 2}}{{cx + b}}\) với \(a\), \(b\), \(c\) là các số thực.
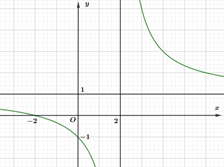
Mệnh đề nào sau đây đúng?
\(a = 2\); \(b = 2\); \(c = - 1\).
\[\left( C \right)\]; \(b = - 2\); \(c = 1\).
\(a = 1\); \(b = 2\); \(c = 1\).
\(a = 1\); \(b = 1\); \(c = - 1\).
Cho hàm số \(y = \frac{{x - a}}{{bx + c}}\) có đồ thị như hình vẽ bên dưới. Tính giá trị của biểu thức \(P = a + b + c\).
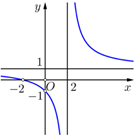
\(P = - 3\).
\(P = 1\).
\(P = 5\).
\(P = 2\).
Tìm giá trị của \(a\), \(b\) để hàm số \(y = \frac{{ax + 2}}{{x - b}}\) có đồ thị như hình vẽ sau:
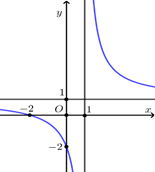
\(\left\{ \begin{array}{l}a = 1\\b = - 1\end{array} \right.\)
\(\left\{ \begin{array}{l}a = - 1\\b = - 1\end{array} \right.\)
\(\left\{ \begin{array}{l}a = 1\\b = 1\end{array} \right.\)
\(\left\{ \begin{array}{l}a = - 1\\b = 1\end{array} \right.\)
Cho hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ.
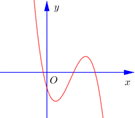
Dấu của \(a\),\(b\),\(c\),\(d\) là
\(a < 0\),\(b < 0\),\(c < 0\),\(d < 0\).
\(a < 0\),\(b < 0\),\(c > 0\),\(d < 0\).
\(a < 0\),\(b > 0\),\(c < 0\),\(d < 0\).
\(a > 0\),\(b > 0\),\(c > 0\),\(d < 0\).
Hình vẽ bên là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\).
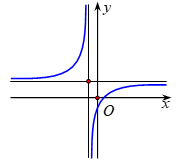
Mệnh đề nào sau đây là đúng?
\(ab < 0\), \(ad < 0\).
\(bd > 0\), \(ad > 0\).
\(ad > 0\), \(ab < 0\).
\(bd < 0\), \(ab > 0\).
Tìm \(a,b\) để hàm số \(y = \frac{{ax + b}}{{x + 1}}\) có đồ thị như hình vẽ bên.
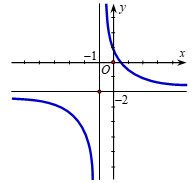
\(a = - 2,b = 1\).
\(a = - 1,b = - 2\).
\(a = 2,b = 1\).
\(a = 1,b = - 2\).
Cho hàm số \[y = a{x^3} + b{x^2} + cx + d\]\[\left( {a \ne 0} \right)\] có đồ thị như hình vẽ bên dưới. Khẳng định nào sau đây đúng ?
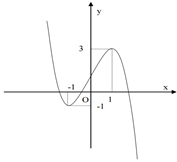
\[a > 0\], \[b < 0\], \[c > 0\], \[d > 0\].
\[a < 0\], \[b < 0\], \[c > 0\], \[d > 0\].
\[a < 0\], \[b = 0\], \[c > 0\], \[d > 0\].
\[a > 0\], \[b > 0\], \[c < 0\], \[d > 0\].
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng?
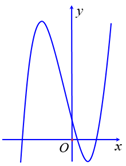
\(a > 0,\,\,b < 0,\,\,c > 0,\,\,d > 0\).
\(a > 0,\,\,b > 0,\,\,c < 0,\,\,d > 0\).
\(a < 0,\,\,b < 0,\,\,c < 0,\,\,d > 0\).
\(a > 0,\,\,b < 0,\,\,c < 0,\,\,d > 0\).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) \(\left( {a \ne 0} \right)\) có đồ thị như hình vẽ dưới đây.
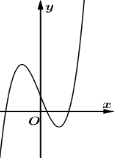
Khẳng định nào sau đây về dấu của \(a,{\rm{ }}b,{\rm{ }}c,{\rm{ }}d\) là đúng nhất ?
\(a,{\rm{ }}b,{\rm{ }}c,{\rm{ }}d > 0\).
\(a,{\rm{ }}d > 0,{\rm{ }}c < 0\).
\(a,{\rm{ }}d > 0\).
\(a > 0,{\rm{ }}c > 0 > b\).
Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\] có đồ thị như hình vẽ. Mệnh đề nào trong các mệnh đề dưới đây là đúng?
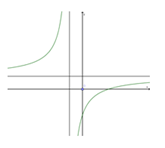
\(ad > 0\), \(bc < 0\).
\(ad < 0\), \(bc > 0\).
\(cd < 0\), \(bd > 0\).
\(ac > 0\), \(ab > 0\).
Hình vẽ bên là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\). Mệnh đề nào sau đây là đúng?
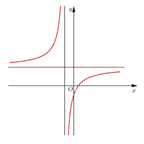
\(ad > 0,\,\,\,ab < 0\).
\(ab < 0,\,\,\,ad < 0\).
\(bd > 0,\,\,\,ad > 0\).
\(bd < 0,\,\,\,ab > 0\).
