7 câu Trắc nghiệm Toán 10 chân trời sáng tạo Hàm số bậc hai có đáp án (Nhận biết)
7 câu hỏi
Cho hàm số y = f(x) = x2 + 3x + 4. Bảng giá trị của hàm số đã cho là:
x | –3 | –2 | \[ - \frac{3}{2}\] | –1 | 0 |
f(x) | 8 | 2 | 1 | 2 | 8 |
x | –3 | –2 | \[ - \frac{3}{2}\] | –1 | 0 |
f(x) | 4 | 6 | 5 | 4 | 6 |
x | –3 | –2 | \[ - \frac{3}{2}\] | –1 | 0 |
f(x) | 4 | 2 | \(\frac{7}{4}\) | 2 | 4 |
x | –3 | –2 | \[ - \frac{3}{2}\] | –1 | 0 |
f(x) | 2 | 4 | \(\frac{7}{4}\) | 2 | 4 |
Trong các hàm số sau đây, hàm số nào là hàm số bậc hai?
f(x) = 3x2 + 2x – 5;
f(x) = 2x – 4;
f(x) = 3x3 + 2x – 1;
f(x) = x4 – x2 + 1.
Cho hàm số y = x2 – 2x có đồ thị (P). Khi đó, tọa độ đỉnh của (P) là:
(0; 0);
(1; –1);
(–1; 3);
(2; 0).
Trục đối xứng của parabol y = –x2 + 5x + 3 là đường thẳng có phương trình:
\(x = \frac{5}{4}\);
\(x = - \frac{5}{2}\);
\(x = - \frac{5}{4}\);
\(x = \frac{5}{2}\).
Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình bên:
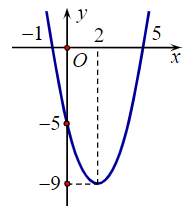
Trục đối xứng của đồ thị hàm số trên là đường thẳng:
x = –9;
x = –5;
x = 0;
x = 2.
Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình vẽ:
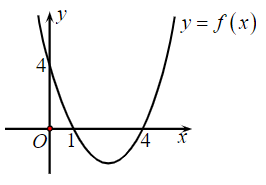
Đặt ∆ = b2 – 4ac. Tìm dấu của a và ∆.
a > 0, ∆ > 0;
a < 0, ∆ > 0;
a > 0, ∆ = 0;
a < 0, ∆ = 0.
Cho hàm số y = –x2 + 5x – 4. Khẳng định nào sau đây đúng?
Hàm số đạt giá trị lớn nhất bằng \(\frac{5}{2}\);
Hàm số đạt giá trị nhỏ nhất bằng \(\frac{5}{2}\);
Hàm số đạt giá trị nhỏ nhất bằng \(\frac{9}{4}\);
Hàm số đạt giá trị lớn nhất bằng \(\frac{9}{4}\).