6 bài tập Một số bài toán thực tế liên quan đến Nguyên hàm (có lời giải)

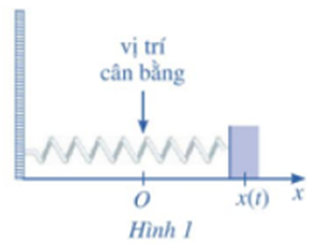
Một con lắc lò xo dao động điều hoà theo phương ngang trên mặt phẳng không ma sát như Hình 1, có vận tốc tức thời cho bởi v(t) = 4cos t, trong đó t tính bằng giây và v(t) tính bằng centimét/giây. Tại thời điểm t = 0, con lắc đó ở vị trí cân bằng. Lập phương trình chuyển động của con lắc đó?

Khi được thả từ độ cao 20m, một vật rơi với gia tốc a = 10 m/s2. Sau khi rơi được t giây thì vật có tốc độ bao nhiêu và đi được quãng đường bao nhiêu?

Một hòn đá rơi từ móm đá có độ cao 150 m so với mặt đất theo phương thẳng đứng. Biết tốc độ rơi của hòn đá (tính theo đơn vị \({\rm{m}}/{\rm{s}}\) ) tại thời điểm t (tính theo giây) được cho bởi công thức \({\rm{v}}({\rm{t}})\) \( = 9,8{\rm{t}}\). Quãng đường rơi được \(S\) của hòn đá tại thời điểm t được cho bởi công thức nào? Sau bao nhiêu giây thì hòn đá chạm đến mặt đất?

Một máy bay di chuyển ra đến đường băng và bắt đầu chạy đà để cất cánh. Giả sử vận tốc của máy bay khi chạy đà được cho bởi v(t)=5+3t (m/s), với t là thời gian (tính bằng giây) kể từ khi máy bay bắt đầu chạy đà. Sau 30 giây thì máy bay cất cánh rời đường băng. Quãng đường máy bay đã di chuyển từ khi bắt đầu chạy đà đến khi rời đường băng là bao nhiêu mét?

Một vườn ươm cây cảnh bán một cây sau 6 năm trồng và uốn tạo dáng. Tốc độ tăng trưởng trong suốt 6 năm được tính xấp xỉ bởi công thức \({h^\prime }(t) = 1,5t + 5\), trong đó \(h(t)({\rm{cm}})\) là chiều cao của cây khi kết thúc \(t\) (năm) (Nguồn: R. Larson and B. Edwards, Calculus 10e Cengage 2014). Cây con khi được trồng cao \(12\;{\rm{cm}}\).

a) Tìm công thức chỉ chiều cao của cây sau \(t\) năm.

b) Khi được bán, cây cao bao nhiêu centimét?