28 câu hỏi
Trong không gian \[Oxyz\], vectơ \[\overrightarrow u = 2\overrightarrow i - 3\overrightarrow k \]có tọa độ là
\[\left( {2;0; - 3} \right)\].
\[\left( { - 2;0;3} \right)\].
\[\left( {2; - 3;0} \right)\].
\[\left( {2;1; - 3} \right)\].
Trong không gian \(Oxyz\), cho điểm \(M\left( {0;\; - 3;\;2} \right)\). Mệnh đề nào dưới đây đúng?
\[\overrightarrow {OM} = - 3\overrightarrow i + 2\overrightarrow j \].
\[\overrightarrow {OM} = - 3\overrightarrow i + 2\overrightarrow j + \overrightarrow k \].
\[\overrightarrow {OM} = - 3\overrightarrow j + 2\overrightarrow k \].
\[\overrightarrow {OM} = - 3\overrightarrow i + 2\overrightarrow k \].
Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(M\left( {2\,;\, - 2\,;\,1} \right)\) trên mặt phẳng \(\left( {Oxy} \right)\) có tọa độ là
\(\left( {2\,;\,0\,;\,1} \right)\).
\(\left( {2\,;\, - 2\,;\,0} \right)\).
\(\left( {0\,;\, - 2\,;\,1} \right)\).
\(\left( {0\,;\,0\,;\,1} \right)\).
Trong không gian \[Oxyz\] với hệ tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j ;\overrightarrow k } \right)\) cho \[\overrightarrow {OA} = \overrightarrow j - 2\overrightarrow i + 5\overrightarrow k .\] Tìm tọa độ điểm \(A\).
\[\left( {5; - 2;1} \right)\].
\[\left( { - 2;1;5} \right)\].
\[\left( {1; - 2;5} \right)\].
\[\left( { - 2;5;1} \right)\].
Trong không gian \(Oxyz\), cho điểm \(A\left( { - 1;3;2} \right)\). Hình chiếu vuông góc của điểm \(A\)trên trục \(Oz\) là điểm
\(M\left( {0;0;2} \right)\).
\(N\left( { - 1;0;0} \right)\).
\(P\left( {0;3;0} \right)\).
\(Q\left( {0;0; - 2} \right)\).
Trong không gian, với hệ trục tọa độ \(Oxyz\) có \(\overrightarrow u = \left( {1;2;5} \right)\). Đẳng thức nào sau đây đúng?
\(\overrightarrow u = - \overrightarrow i - 2\overrightarrow j - 5\overrightarrow k \).
\(\overrightarrow u = \overrightarrow i + 2\overrightarrow j - 5\overrightarrow k \).
\(\overrightarrow u = 2\overrightarrow i + 5\overrightarrow j + \overrightarrow k \).
\(\overrightarrow u = \overrightarrow i + 2\overrightarrow j + 5\overrightarrow k \).
Trong không gian \[{\rm{Ox}}yz\]cho điểm \[A\]thỏa mãn \[\overrightarrow {OA} = 2\overrightarrow i + \overrightarrow j \]với \[\overrightarrow i ,\,\overrightarrow j \]là hai vectơ đơn vị trên hai trục \[Ox\], \[Oy\]. Tọa độ điểm \[A\]là
\[A\left( {2\,;\,1\,;\,0} \right)\].
\[A\left( {0\,;\,2\,;\,1} \right)\].
\[A\left( {0\,;\,1\,;\,1} \right)\].
\[A\left( {1\,;\,1\,;\,1} \right)\].
Trong không gian \[Oxyz\], hình chiếu vuông góc của \[M\left( {1; - 2;3} \right)\]lên mặt phẳng \[\left( {Oyz} \right)\]là
\(A\left( {1; - 2;3} \right)\).
\(A\left( {0; - 2;3} \right)\).
\(A\left( {1; - 2;0} \right)\).
\(A\left( {1;0;3} \right)\).
Trong không gian Oxyz, hình chiếu vuông góc của điểm \(M(3; - 1;2)\)trên mặt phẳng (Oxy) có tọa độ là:
\((0;0;2)\).
\((3;0;2)\).
\((0; - 1;2)\).
\((3; - 1;0)\).
Trong không gian với hệ trục tọa độ \(Oxyz,\) cho \(\overrightarrow a = - \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \) là:
\(\left( {2; - 1; - 3} \right).\)
\(\left( { - 3;2; - 1} \right).\)
\(\left( {2; - 3; - 1} \right).\)
\(\left( { - 1;2; - 3} \right).\)
Trong không gian \[Oxyz\], hình chiếu vuông góc của điểm \(A(3; - 4; - 3)\)trên trục \(Oz\)có tọa độ là
\((0; - 4;0)\).
\((0;0; - 3)\).
\((3; - 4;0)\).
\((3;0;0)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho \(\overrightarrow x = \overrightarrow i - 3\overrightarrow j + 2\overrightarrow k \). Tìm tọa độ của \(\overrightarrow x \)
\[\overrightarrow x = \left( { - 1;3; - 2} \right)\].
\[\overrightarrow x = \left( {1; - 3;0} \right)\].
\[\overrightarrow x = \left( {1; - 3;2} \right)\].
\[\overrightarrow x = \left( { - 1; - 3;2} \right)\].
Trong không gian \[Oxyz\], cho điểm \(M\left( {3;\,2;\, - 1} \right)\). Hình chiếu vuông góc của điểm \(M\)lên trục \(Oz\)là điểm
\({M_3}\left( {3;\,0;\,0} \right)\).
\({M_4}\left( {0;\,2;\,0} \right)\).
\({M_1}\left( {0;\,0;\, - 1} \right)\).
\({M_2}\left( {3;\,2;\,0} \right)\).
Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(N\left( {2; - 2; - 5} \right)\)trên trục \(Ox\)có tọa độ là
\(\left( {2;0;0} \right)\).
\(\left( {2; - 2;0} \right)\).
\(\left( {0; - 2;0} \right)\).
\(\left( {0;0; - 5} \right)\).
Trong không gian \(Oxyz\), cho điểm \(M\left( {2018;\,2019;\,2020} \right)\). Hình chiếu vuông góc của \(M\)trên trục \(Oz\)có tọa độ là
\(\left( {2018;\,0;\,0} \right)\).
\(\left( {0;\,0;\,2020} \right)\).
\(\left( {0;\,2019;\,0} \right)\).
\(\left( {0;\,0;\,0} \right)\).
Trong không gian \[Oxyz\] với hệ tọa độ \[\left( {O;\vec i;\vec j;\vec k} \right)\] cho \[\overrightarrow {OA} = - 2\vec i + 5\vec k\]. Tìm tọa độ điểm \[A\].
\(\left( { - 2;5} \right)\).
\(\left( {5; - 2;0} \right)\).
\(\left( { - 2;0;5} \right)\).
\(\left( { - 2;5;0} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho điểm \[M\left( {1;\,2;\, - 4} \right)\]. Tìm tọa độ hình chiếu vuông góc của điểm \[M\]trên mặt phẳng tọa độ \[\left( {Oxy} \right)\].
\[\left( {1;\,2;\,0} \right)\].
\[\left( {1;\,2;\, - 4} \right)\].
\[\left( {0;\,2;\, - 4} \right)\].
\[\left( {1;\,0;\, - 4} \right)\].
Trong không gian \[Oxyz\], hình chiếu vuông góc của điểm \(M\left( {3\,;\,1\,;\, - 4} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) có tọa độ là
\(\left( { - 3\,;\,1\,;\, - 4} \right)\).
\(\left( {3\,;\,0\,;\,0} \right)\).
\(\left( {0\,;\,1\,;\, - 4} \right)\).
\(\left( {3\,;\, - 1\,;\,4} \right)\).
Trong không gian \({\rm{O}}xyz\), hình chiếu vuông góc của điểm \(A\left( {1;2;3} \right)\) trên mặt phẳng\(\left( {Oyz} \right)\)có tọa độ là
\(\left( {0;\,2;\,3} \right)\).
\(\left( {1;\,0;\,3} \right)\).
\(\left( {1;\,0;\,0} \right)\).
\(\left( {0;\,2;\,0} \right)\).
Trong không gian \[Oxyz\], cho điểm \[A\left( {3; - 1;1} \right)\]. Hình chiếu vuông góc của \[A\] trên mặt phẳng \[ = \int\limits_1^2 {\frac{{\left( {\sqrt {x + 1} - \sqrt x } \right){\rm{d}}x}}{{\sqrt {x\left( {x + 1} \right)} }}} \] là điểm
\[P\left( {0; - 1;0} \right).\]
\[M\left( {3;0;0} \right).\]
\[N\left( {0; - 1;1} \right)\].
\[Q\left( {0;0;1} \right).\]
Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(M\left( {3;4; - 2} \right)\)lên mặt phẳng \(\left( {Oxz} \right)\)có tọa độ là
\(Q\left( {3;0;0} \right)\).
\(G\left( {3;4;0} \right)\).
\(E\left( {0;4; - 2} \right)\).
\(F\left( {3;0; - 2} \right)\).
Trong không gian \[Oxyz\], điểm đối xứng với điểm \(M\left( {2;3; - 1} \right)\)qua trục \[Oy\]có tọa độ là:
\(\left( {0;3;0} \right).\)
\(\left( {2; - 3; - 1} \right).\)
\(\left( { - 2;3;1} \right).\)
\(\left( {0; - 3;0} \right).\)
Trong không gian \[Oxyz\], hình chiếu vuông góc của điểm \[M\left( {3; - 5;1} \right)\]trên mặt phẳng \[\left( {Oyz} \right)\] có tọa độ là:
\[\left( {3;0;1} \right)\].
\[\left( {0; - 5;1} \right)\].
\[\left( {0; - 5;0} \right)\].
\[\left( {0;0;1} \right)\].
Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(E\left( { - 1;3;2} \right)\)trên mặt phẳng \(\left( {Oyz} \right)\)có tọa độ là
\(\left( { - 1;3;0} \right)\).
\(\left( { - 1;0;0} \right)\).
\(\left( {0;3;2} \right)\).
\(\left( { - 1;0;2} \right)\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho \(\overrightarrow a = 2\overrightarrow i + \overrightarrow k - 3\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow a \) là
\(\left( {1;\, - 3;\,2} \right)\).
\[\left( {1;\,2;\, - 3} \right)\].
\[\left( {2;\,1;\, - 3} \right)\].
\(\left( {2; - 3;1} \right)\).
Trong không gian \[Oxyz\], cho hình hộp chữ nhật \(OABC.O'A'B'C'\)có ba đỉnh \(A,\;C,\;O'\)lần lượt nằm trên ba tia \(Ox,\;Oy,\;Oz\)và có ba cạnh \(OA = 6,\;OC = 8,\;OO' = 5\)(tham khảo hình vẽ minh họa). Điểm \(B'\)có tọa độ là
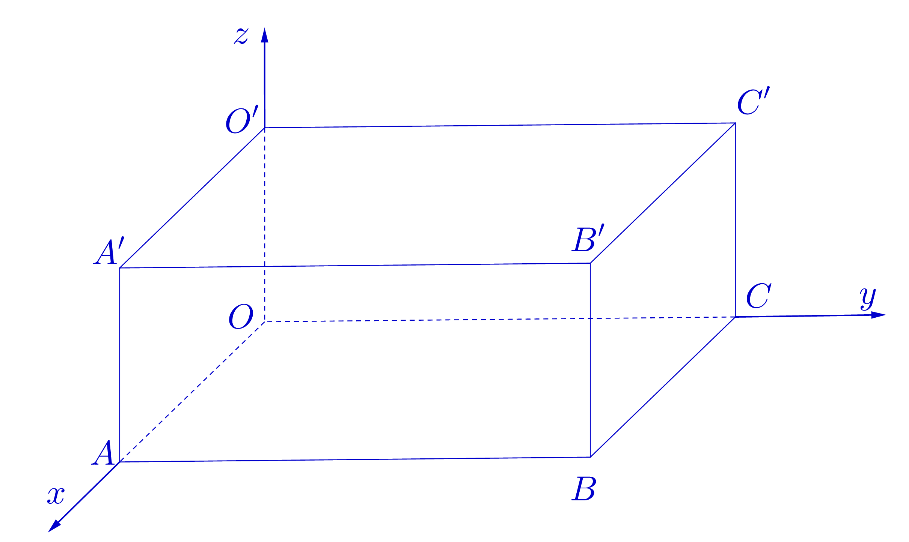
\(\left( {8;\,6;\,5} \right)\).
\(\left( {5;\,6;\,8} \right)\).
\(\left( {6;\,5;\,8} \right)\).
\(\left( {6;\,8;\,5} \right)\).
Trong không gian với hệ toạ độ \(\left( {O;\overrightarrow i ,\overrightarrow j ,\overrightarrow k } \right)\). Nhận xét nào dưới đây sai?
\(\overrightarrow i .\overrightarrow j = 0.\)
\(\overrightarrow j .\overrightarrow k = 0.\)
\(\left| {\overrightarrow i } \right| = 1\).
\(\overrightarrow i .\overrightarrow k = - 1.\)
Trong không gian \(Oxyz\), véctơ đơn vị trên trục \(Oy\) là
\(\overrightarrow j = \left( {0;1;0} \right)\).
\(\overrightarrow i = \left( {1;0;0} \right)\).
\(\overrightarrow k = \left( {0;0;1} \right)\).
\(\overrightarrow n = \left( {1;1;1} \right)\).
