10 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Trong không gian Oxyz, cho vectơ \(\overrightarrow u = 3\overrightarrow i + 4\overrightarrow k - \overrightarrow j \). Tọa độ của vectơ \(\overrightarrow u \) là
(3; −1; 4).
(3; 4; −1).
(4; −1; 3).
(4; 3; −1).
Trong không gian Oxyz, cho điểm M thỏa mãn \(\overrightarrow {OM} = 2\overrightarrow i + \overrightarrow j \). Tọa độ điểm M là
M(0; 2; 1).
M(1; 2; 0).
M(2; 0; 1).
M(2; 1; 0).
Trong không gian Oxyz, xác định tọa độ của điểm A biết A nằm trên tia Ox và OA = 2.
A(0; 0; 2).
A(2; 2; 0).
A(0; 2; 0).
A(2; 0; 0).
Trong không gian Oxyz, cho hai điểm A(1; −1; 2) và B(2; 1; −4). Vectơ \(\overrightarrow {AB} \) có tọa độ là
(−1; −2; 6).
(3; 0; −2).
(1; 0; −6).
(1; 2; −6).
Cho hai điểm A, B thỏa mãn \(\overrightarrow {OA} = \left( {2; - 1;3} \right)\) và \(\overrightarrow {OB} = \left( {5;2; - 1} \right)\).Tìm tọa độ vectơ \(\overrightarrow {AB} \).
(2; −1; 3).
(3; 3; −4).
(7; 1; 2).
(3; −3; 4).
Trong không gian Oxyz, cho hai điểm M và N biết M(2; 1; −1) và \(\overrightarrow {MN} = \left( { - 1;2; - 3} \right)\). Tọa độ N là
N(1; −3; −4).
N(1; 3; −4).
N(−1; 3; −4).
(1; 3; 4).
Hình chiếu vuông góc của điểm A(3; −4; 5) trên mặt phẳng (Oxz) là điểm
M(3; 0; 0).
M(0; −4; 5).
M(0; 0; 5).
M(3; 0; 5).
Trong không gian Oxyz, cho các điểm A(1; 0; 3), B(2; 3; −4), C(−3; 1; 2). Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
D(4; 2; 9).
D(−2; 4; −5).
D(6; 2; −3).
D(−4; −2; 9).
Cho hình hộp ABCD.A'B'C'D' có A(1; 0; 1), B(2; 1; 2), D(1; −1; 1), C'(4; 5; −5). Tìm tọa độ đỉnh C của hình hộp.
C(2; 2; 2).
C(2; 0; 2).
C(2; 2; 0).
C(0; 2; 2).
Trong không gian Oxyz, cho hình hộp chữ nhật OABC.O'A'B'C' có ba đỉnh A, C, O' lần lượt nằm trên ba tia Ox, Oy, Oz và có ba cạnh OA = 6; OC = 8; OO' = 5 (tham khảo hình vẽ mình họa).
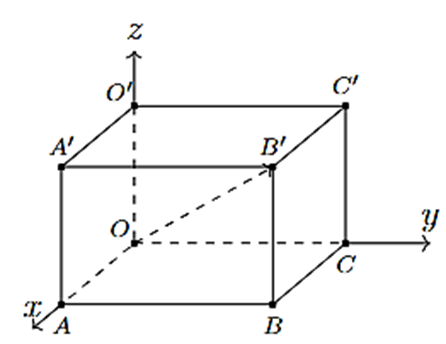
Điểm B' có tọa độ là
(8; 6; 5).
(5; 6; 8).
(6; 5; 8).
(6; 8; 5).
