460 câu trắc nghiệm Xác suất thống kê có đáp án (Phần 10)

Cho X là biến ngẫu nhiên tuân theo phân phối đều rời rạc với n = 5. X∈{1,2,...,5}X∈{1,2,...,5}. Phương sai VX = ?

Cho X là biến ngẫu nhiên tuân theo luật phân phối đều liên tục X∼U([a;b]). Giá trị P(X∈[a−1;b+1]) bằng:

C.

D.

Trong một ban chấp hành đoàn gồm 7 người, cần chọn 3 người trong ban thường vụ. Nếu không có sự phân biệt về chức vụ của 3 người trong ban thường vụ thì có bao nhiêu các chọn?

Một cuộc thi có 15 người tham dự, giả thiết rằng không có hai người nào có điểm bằng nhau. Nếu kết quả cuộc thi và việc chọn ra 4 người có điểm cao nhất thì có bao nhiêu kết quả có thể xảy ra?

Một hộp đựng 5 viên bi màu xanh, 7 viên bi màu vàng. Có bao nhiêu cách lấy ra 6 viên bi bất kỳ?

Có bao nhiêu cách lấy hai con bài từ cỗ bài tú lơ khơ gồm 52 con?

Biến ngẫu nhiên X tuân theo luật phân phối nhị thức: X∼B(n,p).P(X=x), với 0≤x≤n, bằng:

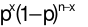
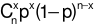
Có 15 đội bóng đá thi đấu theo thể thức vòng tròn tính điểm. Hỏi cần phải tổ chức bao nhiêu trận đấu?

Có bao nhiêu cách cắm 3 bông hoa giống nhau vào 5 lọ khác nhau (mỗi lọ cắm không quá một bông)?

Cho X∼B(5;0.25). Giá trị P(X > 3) bằng:

Cho 10 điểm, không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu đường thẳng khác nhau tạo bởi 2 trong 10 điểm nói trên?

Trong mặt phẳng, cho 6 điểm phân biệt sao cho không có ba điểm nào thẳng hàng. Hỏi có thể lập được bao nhiêu tam giác mà các đỉnh của nó thuộc tập điểm đã cho?

Cho mặt phẳng chứa đa giác đều (H) có 20 cạnh. Xét tam giác có 3 đỉnh được lấy từ các đỉnh của (H). Hỏi có bao nhiêu tam giác có đúng 1 cạnh là cạnh của (H).

Số giao điểm tối đa của 5 đường tròn phân biệt là:

Số giao điểm tối đa của 10 đường thẳng phân biệt là:

Cho hai biến ngẫu nhiên X có phân phối chuẩn 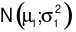, Y có phân phối chuẩn 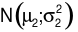, X độc lập với Y. Thống kê  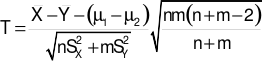có quy luật phân phối?

Với đa giác lồi 10 cạnh thì số đường chéo là:

Trong mặt phẳng có bao nhiêu hình chữ nhật được tạo thành từ bốn đường thẳng phân biệt song song với nhau và năm đường thẳng phân biệt vuông góc với bốn đường thẳng song song đó?

Một lớp có 15 học sinh nam và 20 học sinh nữ. Có bao nhiêu cách chọn 5 bạn học sinh sao cho trong đó có đúng 3 học sinh nữ?

Cho hai biến ngẫu nhiên X có phân phối chuẩn 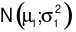, Y có phân phối chuẩn 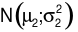, X độc lập với Y. Thống kê 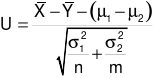có quy luật phân phối

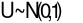
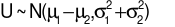
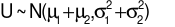
Nếu biến ngẫu nhiên gốc tuân theo phân phối chuẩn 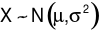 thì 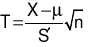tuân theo phân phối?

Một túi đựng 6 bi trắng, 5 bi xanh. Lấy ra 4 viên bi từ túi đó. Hỏi có bao nhiêu cách lấy mà 4 viên bi lấy ra có đủ hai mà?

Một nhóm học sinh có 6 bạn nam và 5 bạn nữ. Hỏi có bao nhiêu cách chọn ra 5 học sinh trong đó có cả nam và nữ?

Một lớp học có 40 học sinh, trong đó có 25 nam và 15 nữ. Giáo viên cần chọn 3 học sinh tham gia vệ sinh công cộng toàn trường. Hỏi có bao nhiêu cách chọn 3 học sinh trong đó có nhiều nhất 1 học sinh nam?

Từ 20 người cần chọn ra một đoàn đại biểu gồm 1 trưởng đoàn, 1 phó đoàn, 1 thư kí và 3 ủy viên. Hỏi có bao nhiêu cách chọn đoàn đại biểu?

Một tổ gồm 10 học sinh. Cần chia tổ đó thành ba nhóm có 5 học sinh, 3 học sinh và 2 học sinh. Số các chia nhóm là:

Trong một giỏ hoa có 5 bông hồng vàng, 3 bông hồng trắng và 4 bông hồng đỏ (các bông hoa coi như đôi một khác nhau). Người ta muốn làm một bó hoa gồm 7 bông được lấy từ giỏ hoa đó. Hỏi có bao nhiêu cách chọn hoa biết bó hoa có đúng 1 bông hồng đỏ?

Nếu biến ngẫu nhiên gốc tuân theo phân phối nhị thức 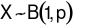 thì khi số lượng mẫu n đủ lớn, biến ngẫu nhiên 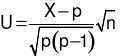tuân theo phân phối?

Một hộp có 6 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Chọn ngẫu nhiên 5 viên bi sao cho có đủ cả ba màu. Số cách chọn là: