4 bài tập Tiệm cận ngang (có lời giải)
4 câu hỏi
Cho hàm số y = \[\frac{{x + 1}}{x}\] có đồ thị như Hình bên dưới.
a) Quan sát đồ thị, hãy cho biết tiệm cận ngang của đồ thị hàm số đã cho và giải thích?
b) Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = 1 tại điểm N (Hình vẽ). Tính MN theo x và nhận xét về MN khi x → +∞ hoặc x → −∞.
Đồ thị của hàm số y = \[\frac{{ - 2x + 1}}{{x + 1}}\] như Hình vẽ bên. Quan sát đồ thị, em hãy cho biết TCN của đồ thị hàm số đã cho? Giải thích?
Tìm tiệm cận ngang của đồ thị các hàm số sau:
a) f (x) = \[\frac{{x - 1}}{{4x + 1}}\];
b) g(x) = \[\frac{{\sqrt x }}{{\sqrt x + 2}}\].
c) h(x) = \[\frac{{ - 3x - 1}}{{x + 1}}\]
Tìm các tiệm cận của đồ thị hàm số như hình vẽ dưới đây và giải thích?
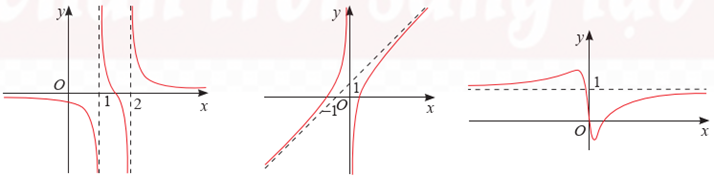
a) \[y = \frac{{2x - 3}}{{5{x^2} - 15x + 10}}\]
b) \[y = \frac{{{x^2} + x - 1}}{x}\]
c) \[y = \frac{{16{x^2} - 8x}}{{16{x^2} + 1}}\]








