38 bài tập Tính xác suất bằng cách sử dụng công thức Bayes (có lời giải)
38 câu hỏi
Khảo sát thị lực của 100 học sinh, ta thu được bảng số liệu sau:
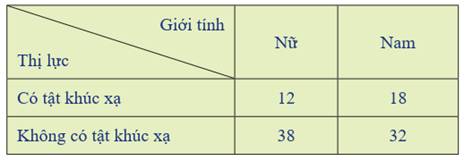
Chọn ngã̃u nhiên 1 bạn trong 100 học sinh trên.
a) Biết rằng bạn đó có tật khúc xạ, tính xác suắt bạn đó là học sinh nam.
b) Biết rằng bạn đó là học sinh nam, tính xác suắt bạn đó có tật khúc xạ.
Một nhà máy có hai phân xường I và II. Phân xường I sản xuất \(40\% \) số sản phẩm và phân xưởng II sản xuất \(60\% \) số sản phẩm. Tỉ lệ sản phẩm bị lỗi của phân xưởng I là \(2\% \) và của phân xưởng II là \(1\% \). Kiểm tra ngẫu nhiên 1 sản phẩm của nhà máy.
a) Tính xác suất để sản phẩm đó bị lỗi.
b) Biết rằng sản phẩm được kiểm tra bị lỗi. Hỏi xác suất sản phẩm đó do phân xưởng nào sản xuất cao hơn?
Một loại xét nghiệm nhanh SARS-CoV-2 cho kết quá dương tính với \(76,2\% \) các ca thực sự nhiểm virus và kết quả âm tích với \(99,1\% \) các ca thực sự không nhiểm virus (nguồn: https://tapchiyhocvietnam.vn/index.php/vmj/article/view/2124/1921). Giả sử tỉ lệ người nhiểm virus SARS-CoV-2 trong một cộng đồng là \(1\% \). Một người trong cộng đồng đó làm xét nghiệm và nhận kết quả dương tính. Hói khả năng người đó thực sự nhiễm virus là cao hay thấp?
Khi phát hiện một vật thể bay, xác suất một hệ thống radar phát cảnh báo là 0,9 nếu vật thể bay đó là mục tiêu thật và là 0,05 nếu đó là mục tiêu giả. Có \(99\% \) các vật thể bay là mục tiêu giả. Biết rằng hệ thống radar đang phát cảnh báo khi phát hiện một vật thể bay. Tính xác suất vật thể đó là mục tiêu thật.

Người ta điều tra thấy ở một địa phương nọ có \(2\% \) tài xế sử dụng điện thoại di động khi lái xe. Trong các vụ tai nạn ở địa phương đó, người ta nhận thấy có \(10\% \) là do tài xế có sử dụng điện thoại khi lái xe gây ra. Hỏi việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần?

Cho hai biến cố \(A\), \(B\) sao cho \({\rm{P}}(A) = 0,6\); \({\rm{P}}(B) = 0,4;{\rm{P}}(A\mid B) = 0,3\). Tính \({\rm{P}}(B\mid A)\).
Cho hai biến cố \(A\), \(B\) sao cho \({\rm{P}}(A) = 0,4\); \({\rm{P}}(B) = 0,8;{\rm{P}}(B\mid A) = 0,3\). Tính \({\rm{P}}(A\mid B)\).
Cho hai biến cố \(A\), \(B\) với \({\rm{P}}(B) = 0,6;{\rm{P}}(A\mid B) = 0,7\) và \({\rm{P}}(A\mid \bar B) = 0,4\). Tính \({\rm{P}}(A)\).
Cho hai biến cố xung khắc \(A\), \(B\) với \({\rm{P}}(A) = 0,2;{\rm{P}}(B) = 0,4\). Tính \({\rm{P}}(A\mid B)\).
Có hai chiếc hộp, hộp I chứa 5 viên bi màu trắng và 5 viên bi màu đen, hộp II chứa 6 viên bi màu trắng và 4 viên bi màu đen, các viên bi có cùng kích thước và khối lượng. Lấy ngẫu nhiên một viên bi từ hộp I bỏ sang hộp II . Sau đó lấy ra ngẫu nhiên một viên bi từ hộp II.
a) Tính xác suất để viên bi được lấy ra từ hộp II là viên bi màu trắng.
b) Giả sử viên bi được lấy ra từ hộp II là viên bi màu trắng. Tính xác suất để viên bi màu trắng đó thuộc hộp I .
Một loại linh kiện do hai nhà máy I, II cùng sản xuất. Tî lệ phế phẩm của các nhà máy \({\rm{I}},{\rm{II}}\) lần lượt là: 0,04 ; 0,03. Trong một lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy I và 120 sản phẩm của nhà máy II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó.
a) Tính xác suất để linh kiện được lấy ra không phải là phế phẩm.
b) Giả sử linh kiện được lấy ra là linh kiện phế phẩm. Hỏi xác suất linh kiện đó do nhà máy nào sản xuất là cao hơn?
Năm 2001, Cộng đồng châu Âu có làm một đợt kiểm tra rất rộng rãi các con bò để phát hiện những con bị bệnh bò điên. Không có xét nghiệm nào cho kết quả chính xác \(100\% \). Một loại xét nghiệm, mà ở đây ta gọi là xét nghiệm A , cho kết quả như sau: Khi con bò bị bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm \({\rm{Al\`a }}70\% \), còn khi con bò không bị bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm A là \(10\% \). Biết rằng tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 13 con trên 1000000 con (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics - Understanding why and how, Springer, 2005). Hỏi khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là bao nhiêu?
Có hai chiếc hộp, hộp I có 5 viên bi màu trắng và 5 viên bi màu đen, hộp II có 6 viên bi màu trắng và 4 viên bi màu đen, các viên bi có cùng kích thược và khối lượng. Lấy ngẫu nhiên đồng thời hai viên bi từ hộp I bỏ sang hộp II. Sau đó lấy ngẫu nhiên một viên bi từ hộp II.
a) Tính xác suất để viên bi được lấy ra là viên bi màu trắng.
b) Giả sử viên bi được lấy ra là viên bi màu trắng. Tính xác suất viên bi màu trắng đó thuộc hộp I.
Một loại linh kiện do hai nhà máy số I , số II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy \({\rm{I}},{\rm{II}}\) lần lượt là: \(4\% ;3\% \). Trong một lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số I và 120 sản phẩm của nhà máy số II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó.
a) Tính xác suất để linh kiện được lấy ra là linh kiện tốt.
b) Giả sử linh kiện được lấy ra là linh kiện phế phẩm. Xác suất linh kiện đó do nhà máy nào sản xuất là cao nhất?
Kết quả khảo sát tại một xã cho thấy có \(20\% \) cư dân hút thuốc lá. Tỉ lệ cư dân thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp trong số những người hút thuốc lá và không hút thuốc lá lần lượt là \(70\% ,15\% \).
a) Nếu ta gặp một cư dân của xã thì xác suất người đó thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp là bao nhiêu?
b) Nếu ta gặp một cư dân của xã thường xuyên gặp các vấn đề sức khoẻ vể đường hô hấp thì xác suất người đó có hút thuốc lá là bao nhiêu?
Giả sử trong một nhóm 80 người có 69 người không nhiễm bệnh và 11 người nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh, xác suất xét nghiệm có kết quả dương tính là 0,9 ; còn đối với người không nhiễm bệnh, xác suất xét nghiệm có kết quả dương tính là 0,05 .
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Giả sử X là một người trong nhóm bị xét nghiệm có kết quả dương tính. Tính xác suất để X là người nhiễm bệnh.
Một chiếc hộp có 20 chiếc thẻ cùng loại, trong đó có 2 chiếc thẻ màu xanh và 18 chiếc thẻ màu trắng. Bạn Châu rút thẻ hai lần một cách ngẫu nhiên, mỗi lần rút một thẻ và thẻ được rút ra không bỏ lại hộp. Tính xác suất để cả hai lần bạn Châu đều rút được thẻ màu xanh. Năm 2001 , Cộng đồng châu Âu có làm một đợt kiểm tra rất rộng rãi các con bò để phát hiện những con bị bệnh bò điên. Không có xét nghiệm nào cho kết quả chính xác \(100\% \). Một loại xét nghiệm, mà ở đây ta gọi là xét nghiệm A , cho kết quả như sau: khi con bò bị bệnh bò điền thì xác suất để có phản ứng dương tính trong xét nghiệm A là \(70\% \), còn khi con bò không bị bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm A là \(10\% \). Biết rằng tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 13 con trên 1000000 con (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics Understanding why and how, Springer, 2005). Hỏi khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là bao nhiêu?
Một cửa hàng kinh doanh tổ chức rút thăm trúng thưởng cho hai loại sản phẩm. Tỉ lệ trúng thưởng của các loại sản phẩm \({\rm{I}},{\rm{II}}\) lần lượt là: \(6\% ;4\% \). Trong một hộp kín gồm các thăm cùng loại, người ta để lẫn lộn 200 chiếc thăm cho sản phẩm loại I và 300 chiếc thăm cho sản phẩm loại II . Một khách hàng lấy ngẫu nhiên 1 chiếc thăm từ chiếc hộp đó.
a) Tính xác suất để chiếc thăm được lấy ra là trúng thưởng.
b) Giả sử chiếc thăm được lấy ra là trúng thưởng. Xác suất chiếc thăm đó thuộc loại sản phẩm nào là cao nhất?
Một xạ thủ bắn vào bia số 1 và bia số 2 . Xác suất để xạ thủ đó bắn trúng bia số 1 , bia số 2 lần lượt là 0,8 ; 0,9. Xác suất để xạ thủ đó bắn trúng cả hai bia là 0,8 . Xét hai biến cố sau:
A: "Xạ thủ đó bắn trúng bia số 1";
B: "Xạ thủ đó bắn trúng bia số 2".
a) Hai biến cố \(A\) và \(B\) có độc lập hay không?
b) Biết xạ thủ đó bắn trúng bia số 1 , tính xác suất xạ thủ đó bắn trúng bia số 2 .
c) Biết xạ thủ đó không bắn trúng bia số 1, tính xác suất xạ thủ đó bắn trúng bia số 2 .
Một chiếc hộp có 40 viên bi, trong đó có 12 viên bi màu đỏ và 28 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Bạn Ngân lấy ngẫu nhiên viên bi từ chiếc hộp đó hai lần, mỗi lần lấy ra một viên bi và viên bi được lấy ra không bỏ lại hộp. Tính xác suất để cả hai lần bạn Ngân đều lấy ra được viên bi màu vàng.
Giả sử trong một nhóm người có 2 người nhiễm bệnh, 58 người còn lại là không nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh, xác suất xét nghiệm có kết quả dương tính là \(85\% \), nhưng đối với người không nhiễm bệnh thì xác suất để bị xét nghiệm có phản ứng dương tính là \(7\% \).
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Giả sử X là một người trong nhóm bị xét nghiệm có kết quả dương tính. Tính xác suất để X là người nhiễm bệnh.
Giả sử có một loại bệnh mà tỉ lệ người mắc bệnh là \(0,1\% \). Giả sử có một loại xét nghiệm, mà ai mắc bệnh khi xét nghiệm cũng có phản ứng dương tính, nhưng tỉ lệ phản ứng dương tính giả là \(5\% \) (tức là trong số những người không bị bệnh có \(5\% \) số người xét nghiệm lại có phản ứng dương tính).
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Khi một người xét nghiệm có phản ứng dưởg tính thì khả năng mắc bệnh của người đó là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm)?
Được biết có \(5\% \) đàn ông bị mù màu, và \(0,25\% \) phụ nữ bị mù màu (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics - Understanding why and how, Springer, 2005). Giả sử số đàn ông bằng số phụ nữ. Chọn một người bị mù màu một cách ngẫu nhiên. Hỏi xác suất để người đó là đàn ông là bao nhiêu?
Hộp thứ nhất có 3 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 7 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ hai.
a) Tính xác suất để hai viên bi lấy ra từ hộp thứ hai là bi đỏ.
b) Biết rằng 2 viên bi lấy ra từ hộp thứ hai là bi đỏ, tính xác suất viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ.
Trong một trường học, tì lệ học sinh nữ là \(52\% \). Tì lệ học sinh nữ và tì lệ học sinh nam tham gia câu lạc bộ nghệ thuật lần lượt là \(18\% \) và \(15\% \). Chọn ngẫu nhiên 1 học sinh của trường.
a) Tính xác suất học sinh được chọn có tham gia câu lạc bộ nghệ thuật.
b) Biết rằng học sinh được chọn có tham gia câu lạc bộ nghệ thuật. Tính xác suất học sinh đó là nam.
Tỉ lệ người dân đã tiêm vắc xin phòng bệnh A ở một địa phương là \(65\% \). Trong số những người đã tiêm phòng, tì lệ mắc bệnh A là \(5\% \); trong số những người chưa tiêm phòng, tỉ lệ mắc bệnh A là \(17\% \). Chọn ngấu nhiên một người ở địa phương đó.
a) Tính xác suất người được chọn mắc bệnh A .
b) Biết rằng người được chọn mắc bệnh A . Tính xác suất người đó chưa tiêm vắc xin phòng bệnh A .
Ở một khu rừng nọ có 7 chú lùn, trong đó có 4 chú luôn nói thật, 3 chú còn lại luôn tự nhận mình nói thật nhưng xác suất để mỗi chú này nói thật là 0,5 . Bạn Tuyết gặp ngẫu nhiên một chú lùn. Gọi \(A\) là biến cố "Chú lùn đó luôn nói thật" và \(B\) là biến cố "Chú lùn đó tự nhận mình luôn nói thật".
a) Tính xác suất của các biến cố \(A\) và \(B\).
b) Biết rằng chú lùn mà bạn Tuyết gặp tự nhận mình là người luôn nói thật. Tính xác suất để chú lùn đó luôn nói thật.
Trong một kì thi tốt nghiệp trung học phổ thông, một tỉnh \(X\) có 80 % học sinh lựa chọn tổ hợp A 00 (gồm các môn Toán, Vật lí, Hoá học). Biết rằng, nếu một học sinh chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là 0,6 ; còn nếu một học sinh không chọn tổ hợp A 00 thì xác suất để học sinh đó đỗ đại học là 0,7 . Chọn ngẫu nhiền một học sinh của tỉnh X đã tốt nghiệp trung học phổ thông trong kì thi trên. Biết rằng học sinh này đã đỗ đại học. Tính xác suất để học sinh đó chọn tổ hợp A00.
Trong một kho rượu có \(30\% \) là rượu loại I. Chọn ngã̃u nhiên một chai rượu đưa cho ông Tùng, một người sành rượu, để nếm thử. Biết rằng, một chai rượu loại I có xác suất 0,9 để ông Tùng xác nhận là loại I ; một chai rượu không phải loại I có xác suất 0,95 để ông Tùng xác nhận đây không phải là loại I. Sau khi nếm, ông Tùng xác nhận đây là rượu loại I. Tính xác suất để chai rượu đúng là rượu loại I.
Trong \(Y\) học, để chẩn đoán bệnh \(X\) nào đó, người ta thường dùng một xét nghiệm. Xét nghiệm dương tính, tức là xét nghiệm đó kết luận một người mắc bệnh \(X\). Xét nghiệm âm tính, tức là xét nghiệm đó kết luận một người không mắc bệnh \(X\). Vỉ không có một xét nghiệm nào tuyệt đối đưng nên trên thực tế có thể xảy ra hai sai lầm sau:
- Xét nghiệm dương tính nhưng thực tế người xét nghiệm không mắc bệnh. Ta gọi đây là dương tính giả.
- Xét nghiệm âm tính nhưng thực tế người xét nghiệm lại mắc bệnh. Ta gọi đây là âm tính giả.
Ông \(M\) đi xét nghiệm bệnh hiểm nghèo \(X\). Biết rằng, nếu một người mắc bệnh \(X\) thì với xác suất 0,95 xét nghiệm cho dương tính; nếu một người không bị bệnh \(X\) thì với xác suất 0,01 xét nghiệm cho dương tính.
Xét nghiệm của ông \(M\) cho kết quả dương tính. Ông \(M\) hoảng hốt khi nghĩ rằng mình có xác suất 0,95 mắc bệnh hiểm nghèo \(X\).
Trong tình huống mở đầu Muc 2, gọi A là biến cố: "Ông M mắc bệnh hiểm nghèo X"; B là biến cố: "Xét nghiệm cho kết quả dương tính".
a) Nêu các nội dung còn thiếu tương ứng với "(?)" để hoàn thành các câu sau đây:
là xác suất để (?) với điều kiện (?);
là xác suất để (?) với điều kiện (?).
b) 0,95 là \(P(A\mid B)\) hay \(P(B\mid A)\) ? Có phải ông \(M\) có xác suất 0,95 mắc bệnh hiểm nghèo \(X\) không?
c) Tính xác suất để ông M mắc bệnh hiểm nghèo X nếu kết quả xét nghiệm cho kết quả dương tính.
Trong \(Y\) học, để chẩn đoán bệnh \(X\) nào đó, người ta thường dùng một xét nghiệm. Xét nghiệm dương tính, tức là xét nghiệm đó kết luận một người mắc bệnh \(X\). Xét nghiệm âm tính, tức là xét nghiệm đó kết luận một người không mắc bệnh \(X\). Vỉ không có một xét nghiệm nào tuyệt đối đưng nên trên thực tế có thể xảy ra hai sai lầm sau:
- Xét nghiệm dương tính nhưng thực tế người xét nghiệm không mắc bệnh. Ta gọi đây là dương tính giả.
- Xét nghiệm âm tính nhưng thực tế người xét nghiệm lại mắc bệnh. Ta gọi đây là âm tính giả.
Ông \(M\) đi xét nghiệm bệnh hiểm nghèo \(X\). Biết rằng, nếu một người mắc bệnh \(X\) thì với xác suất 0,95 xét nghiệm cho dương tính; nếu một người không bị bệnh \(X\) thì với xác suất 0,01 xét nghiệm cho dương tính.
Xét nghiệm của ông \(M\) cho kết quả dương tính. Ông \(M\) hoảng hốt khi nghĩ rằng mình có xác suất 0,95 mắc bệnh hiểm nghèo \(X\).
Thống kê cho thấy tỉ lệ dân số mắc bệnh hiểm nghèo X là \(0,2\% \).
a) Trước khi tiến hành xét nghiệm, xác suất mắc bệnh hiểm nghèo \(X\) của ông M là bao nhiêu?
b) Sau khi xét nghiệm cho kết quả dương tính, xác suất mắc bệnh hiểm nghèo \(X\) của ông M là bao nhiêu?
Một thống kê cho thấy tỉ lệ dân số mắc bệnh hiểm nghèo Y là \(0,5\% \). Bà N đi xét nghiệm bệnh hiểm nghèo \(Y\) và nhận được kết quả là âm tính. Biết rằng, nếu mắc bệnh hiểm nghèo \(Y\) thì với xác suất 0,94 xét nghiệm là dương tính; nếu không bị bệnh hiểm nghèo \(Y\) thì với xác suất 0,97 xét nghiệm là âm tính.
a) Trước khi tiến hành xét nghiệm xác suất không mắc bệnh hiểm nghèo Y của bà N là bao nhiêu?
b) Sau khi xét nghiệm cho kết quả âm tính, xác suất không mắc bệnh hiểm nghèo Y của bà N là bao nhiêu?
Có hai đội thi đấu môn Bắn súng. Đội I có 5 vận động viên, đội II có 7 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội ll tương ứng là 0,65 và 0,55 . Chọn ngẫu nhiên một vận động viên.
a) Tính xác suất để vận động viên này đạt huy chương vàng;
b) Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội \(I\).
Một bộ lọc được sử dụng để chặn thư rác trong các tài khoản thư điện tử. Tuy nhiên, vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất 0,95 và một thư đúng (không phải là thư rác) bị chặn với xác suất 0,01 . Thống kê cho thấy tỉ lệ thư rác là \(3\% \).
a) Chọn ngẫu nhiên một thư bị chặn. Tính xác suất để đó là thư rác.
b) Chọn ngẫu nhiên một thư không bị chặn. Tính xác suất để đó là thư đúng.
c) Trong số các thư bị chặn, có bao nhiêu phần trăm là thư đúng? Trong số các thư không bị chặn, có bao nhiêu phần trăm là thư rác?
Một loại vaccine được tiêm ở địa phương X. Người có bệnh nền thì với xác suất 0,35 có phản ứng phụ sau tiêm; người không có bệnh nền thì chỉ có phản ứng phụ sau tiêm với xác suất 0,16 . Chọn ngẫu nhiên một người được tiêm vaccine và người này có phản ứng phụ. Tính xác suất để người này có bệnh nền, biết rằng tỉ lệ người có bệnh nền ở địa phương X là \(18\% \).
Có hai cái hộp giống nhau, hộp thứ nhất chứa 5 quả bóng bàn màu trắng và 3 quả bóng bàn màu vàng, hộp thứ hai chứa 4 quả bóng bàn màu trắng và 6 quả bóng bàn màu vàng. Các quả bóng có cùng kích thước và khối lượng. Minh lấy ra ngẫu nhiên 1 quả bóng từ hộp thứ nhất. Nếu quả bóng đó là bóng vàng thì Minh lấy ra ngẫu nhiên đồng thời 2 quả bóng từ hộp thứ hai; nếu quả bóng đó màu trắng thì Minh lấy ra ngẫu nhiên đồng thời 3 quả bóng từ hộp thứ hai.
a) Sử dụng sơ đồ hình cây, tính xác suất để có đúng 1 quả bóng màu vàng trong các quả bóng lấy ra từ hộp thứ hai.
b) Biết rằng các quả bóng lấy ra từ hộp thứ hai đều có màu trắng. Tính xác suất để quả bóng lấy ra từ hộp thứ nhất có màu vàng.
Hộp thứ nhất có 1 viên bi xanh và 5 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 5 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên đồng thời hai viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ hai.
a) Tính xác suất để hai viên bi lấy ra từ hộp thứ hai là bi đỏ.
b) Biết rằng 2 viên bi lấy ra từ hộp thứ hai là bi đỏ. Tính xác suất để 2 viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ.
Một doanh nghiệp có \(45\% \) nhân viên là nữ. Tỉ lệ nhân viên nữ và tỉ lệ nhân viên nam mua bảo hiểm nhân thọ lần lượt là \(7\% \) và \(5\% \). Chọn ngẫu nhiền một nhân viên của doanh nghiệp.
a) Tính xác suất nhân viên được chọn có mua bảo hiểm nhân thọ.
b) Biết rằng nhân viên được chọn có mua bảo hiểm nhân thọ. Tính xác suất nhân viên đó là nam.






