20 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài 2. Công thức xác suất toàn phần và công thức Bayes (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hai biến cố A, B thỏa mãn P(A) = 0,3; P(B) = 0,2 và \(P\left( {A|B} \right) = 0,15\). Khi đó \(P\left( {B|A} \right)\)bằng
0,1.
0,4.
0,225.
0,009.
Cho \(P\left( A \right) = 0,35;P\left( {B|A} \right) = 0,4;P\left( {B|\overline A } \right) = 0,3\). Giá trị của \(P\left( {A|B} \right)\) là
\(\frac{1}{2}\).
\(\frac{8}{{13}}\).
\(\frac{1}{4}\).
\(\frac{{28}}{{67}}\).
Cho sơ đồ hình cây như hình. Tính P(B).
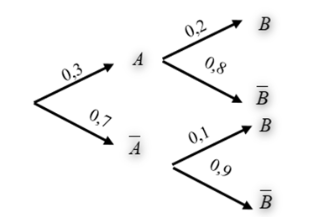
0,2.
0,1.
0,13.
0,8.
Một nhà máy có hai phân xưởng I và II. Phân xưởng I sản xuất 40% số sản phẩm và phân xưởng II sản xuất 60% số sản phẩm. Tỉ lệ sản phẩm bị lỗi của phân xưởng I là 2% và của phân xưởng II là 1%. Kiểm tra ngẫu nhiên 1 sản phẩm của nhà máy và xác suất để sản phẩm đó bị lỗi là
0,02.
0,6.
0,014.
0,01.
Một bệnh viên có hai phòng khám là phòng A và phòng B với khả năng lựa chọn của bệnh nhân là như nhau. Tỉ lệ bệnh nhân nam có ở phòng A và phòng B lần lượt là 60% và 40%. Một người bệnh được chọn ngẫu nhiên từ hai phòng khám. Tính xác suất để người bệnh được chọn là nam.
0,6.
0,5.
0,4.
0,3.
Cho A, B là hai biến cố. Biết P(B) = 0,2. Nếu B không xảy ra thì tỉ lệ A xảy ra là 2%. Nếu B xảy ra thì tỉ lệ A xảy ra 4%. Xác suất của biến cố A là bao nhiêu?
0,018.
0,036.
0,028.
0,024.
Có hai máy sản xuất ly nhựa, trong đó máy I sản xuất 60%, máy II sản xuất 40% ly nhựa. Tỉ lệ ly nhựa bị hư của các máy lần lượt là 0,5% và 0,8%. Chọn ngẫu nhiên 1 ly nhựa để kiểm tra. Tính xác suất để chọn được ly nhựa hư do máy I sản xuất.
0,6.
0,005.
0,003.
0,0062.
Có hai chiếc hộp đựng 30 chiếc bút chì có hình dáng, kích thước giống nhau. Sau khi thống kê nhận được bảng số liệu về màu sắc và số lượng bút như sau:
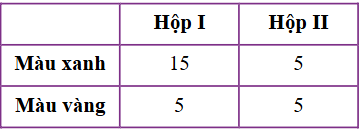
Lấy ngẫu nhiên một chiếc bút từ hộp I bỏ sang hộp II. Sau đó, lấy ngẫu nhiên một chiếc bút từ hộp II. Xác suất để chiếc bút lấy ra từ hộp II có màu xanh là
\(\frac{3}{4}\).
\(\frac{1}{4}\).
\(\frac{6}{{11}}\).
\(\frac{{23}}{{44}}\).
Cho bảng dữ liệu sau về kết quả xét nghiệm một loại bệnh
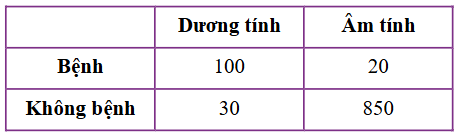
Nếu một người có kết quả xét nghiệm dương tính, xác suất người đó thực sự mắc bệnh là bao nhiêu?
10%.
77%.
90%.
50%.
Được biết có 5% đàn ông bị mù màu và 0,25% phụ nữ bị mù màu. Giả sử số đàn ông bằng số phụ nữ. Chọn ngẫu nhiên một người bị mù màu. Xác suất để người được chọn là đàn ông bằng bao nhiêu?
\(\frac{{20}}{{23}}\).
\(\frac{{19}}{{21}}\).
\(\frac{{19}}{{23}}\).
\(\frac{{20}}{{21}}\).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Một phân xưởng có 80% công nhân là nữ. Tỉ lệ công nhân nữ có tay nghề cao là 40%, tỉ lệ công nhân nam có tay nghề cao là 55%. Chọn ngẫu nhiên 1 công nhân của phân xưởng. Gọi A là biến cố “Công nhân được chọn là nữ” và B là biến cố “Công nhân được chọn có tay nghề cao”. Khi đó:
a) Xác suất của biến cố \(\overline A \) là 0,8.
b) Xác suất của biến cố B là 0,43.
c) A và B là hai biến cố độc lập.
d) Xác suất của biến cố A với điều kiện B là \(\frac{{11}}{{43}}\).
Kết quả khảo sát những bệnh nhân bị đột quỵ của một bệnh viện cho thấy tỉ lệ bệnh nhân hồi phục sau đột quỵ là 35%; tỉ lệ bệnh nhân được điều trị trong 6 giờ đầu sau khi đột quỵ là 40%; tỉ lệ bệnh nhân được điều trị trong 6 giờ đầu sau khi đột quỵ và hồi phục là 30%. Chọn ngẫu nhiên một bệnh nhân bị đột quỵ được điều trị tại bệnh viện. Khi đó:
a) Xác suất người đó được điều trị trong 6 giờ đầu sau khi đột quỵ, biết rằng người đó hồi phục là 0,6.
b) Xác suất người đó không hồi phục, biết rằng người đó được điều trị trong 6 giờ đầu sau khi đột quỵ là 0,4.
c) Xác suất người đó hồi phục, biết rằng người đó không được điều trị trong 6 giờ đầu sau khi đột quỵ là \(\frac{1}{{25}}\).
d) Việc đưa bệnh nhân vào bệnh viện để điều trị trong 6 giờ đầu sau khi đột quỵ làm tăng tỉ lệ hồi phục lên \(\frac{{10}}{3}\) lần.
Một kho hàng có 85% sản phẩm loại I và 15% sản phẩm loại II, trong đó có 1% sản phẩm loại I bị hỏng, 4% sản phẩm loại II bị hỏng. Các sản phẩm có kích thước và hình dạng như nhau. Một khách hàng chọn ngẫu nhiên 1 sản phẩm. Xét các biến cố:
A: “Khách hàng chọn được sản phẩm loại I”;
B: “Khách hàng chọn được sản phẩm không bị hỏng”.
a) P(A) = 0,85.
b) \(P\left( {B|A} \right) = 0,99\).
c) P(B) = 0,9855.
d) \(P\left( {A|B} \right) = 0,95\).
Một tiệm photocopy có hai máy I và II. Máy I photo 40% số lượng sản phẩm và máy II photo 60% số lượng sản phẩm. Có 4% sản phẩm do máy I photo bị lỗi và 5% sản phẩm do máy II photo bị lỗi. Một sản phẩm được lấy ra ngẫu nhiên để kiểm tra.
a) Nếu sản phẩm được photo bởi máy I thì xác suất sản phẩm đó bị lỗi là 0,04.
b) Xác suất để sản phẩm lấy ra được photo bởi máy II và không bị lỗi là 0,384.
c) Xác suất để sản phẩm lấy ra không bị lỗi là 0,046.
d) Nếu sản phẩm lấy ra bị lỗi, xác suất để nó được photo bởi máy II bằng \(\frac{{15}}{{23}}\).
Một chiếc hộp có 80 viên bi, trong đó có 50 viên bi màu đỏ và 30 viên bi màu vàng, các viên bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có 60% số viên bi màu đỏ có đánh số và 50% số viên bi màu vàng có đánh số, những viên bi còn lại không đánh số.
a) Số viên bi màu đỏ có đánh số là 30.
b) Số viên bi không đánh số là 35.
c) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra có đánh số là \(\frac{3}{5}\).
d) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra không đánh số là \(\frac{7}{{16}}\).
PHẦN III. TRẢ LỜI NGẮN
Trong một cuộc khảo sát về việc có chơi thể thao hay không có 40% nam và 60% nữ tham gia. Kết quả cho thấy có 30% nam và 50% nữ không chơi thể thao. Chọn ngẫu nhiên một người trong số người được khảo sát. Biết người đó chơi thể thao. Tính xác suất để người được chọn là nam (kết quả làm tròn đến hàng phần trăm).
Một công ty thời trang có hai chi nhánh cùng sản xuất một loại áo thời trang, trong đó có 56% áo thời trang ở chi nhánh I và 44% áo thời trang ở chi nhánh II. Tại chi nhánh I có 75% áo chất lượng cao và tại chi nhánh II có 68% áo chất lượng cao (kích thước và hình dạng bề ngoài của các áo là như nhau). Chọn ngẫu nhiên 1 áo thời trang. Xác suất chọn được áo chất lượng cao là bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
Có hai chiếc hộp, hộp I có 5 viên bi màu trắng và 5 viên bi màu đen, hộp II có 6 viên bi màu trắng và 4 viên bi màu đen, các viên bi có cùng kích thước và khối lượng. Lấy ngẫu nhiên một viên bi từ hộp I bỏ sang hộp II. Sau đó lấy ngẫu nhiên một viên bi từ hộp II. Biết viên bi lấy ra từ hộp II là viên bi màu trắng. Xác suất viên bi đó là viên bi của hộp I bỏ sang có dạng \(\frac{a}{b}\) với \(a,b \in \mathbb{Z}\) và \(\frac{a}{b}\) là phân số tối giản. Tính giá trị của biểu thức \(S = {a^2} + {b^2}\).
Thống kê hồ sơ 250 học sinh khối 10 trong đó có 150 học sinh nữ và 100 học sinh nam. Sau khi thống kê, kết quả có 60% học sinh nữ là đoàn viên, 50% học sinh nam là đoàn viên; những học sinh còn lại không là đoàn viên. Chọn ngẫu nhiên một học sinh trong 250 học sinh khối 10. Tính xác suất để học sinh được chọn là đoàn viên.
Một lớp học có số học sinh nữ chiếm 45% tổng số học sinh cả lớp. Cuối năm tổng kết, lớp học đó có tỉ lệ học sinh giỏi là nữ là 30%, học sinh giỏi là nam chiếm 40%. Giáo viên chủ nhiệm cần chọn 1 học sinh của lớp để đại diện cho lớp lên nhận thưởng. Biết rằng học sinh được chọn là học sinh giỏi. Tính xác suất để em đó là nữ (làm tròn kết quả đến hàng phần trăm).






