25 câu trắc nghiệm Toán 11 Kết nối tri thức bài 7: Cấp số nhân có đáp án
25 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
Trong các dãy số sau, dãy số nào là một cấp số nhân?
\[{\rm{128;}} - {\rm{64; 32;}} - {\rm{16;}} - {\rm{8; }}...\]
\[\sqrt {\rm{2}} {\rm{; 2; 4; 4}}\sqrt {\rm{2}} {\rm{; }}...\]
\[{\rm{5; 6; 7; 8; }}...\]
\[{\rm{15; 5; 1; }}\frac{{\rm{1}}}{{\rm{5}}}{\rm{; }}...\]
Cho cấp số nhân (un) với u1 = 2 và công bội \(q = \frac{1}{2}\). Tính u5.
8.
\(\frac{1}{8}\).
2.
\(\frac{1}{2}\).
Cho một cấp số nhân có số hạng đầu u1 = 5, công bội q = 2. Khi đó số hạng tổng quát của cấp số nhân đó là
un = 5.2n.
un = 5.2n – 1.
un = 5.2n + 1.
un = 2.5n – 1.
Cho cấp số nhân (un) với u1 = −2 và q = −5. Viết bốn số hạng đầu tiên của cấp số nhân.
−2; 10; 50; −250.
−2; 10; −50; 250.
−2; −10; −50; −250.
−2; 10; 50; 250.
Với giá trị x nào dưới đây thì các số −4; x; −9 theo thứ tự lập thành một cấp số nhân.
\[{\rm{x = }} - 6\].
\[{\rm{x = }} - \frac{{13}}{2}\].
\[{\rm{x = }} \pm 6\].
x = 36.
Cho cấp số nhân (un) với u1 = 2 và u4 = 54. Giá trị của công bội q bằng
3.
9.
27.
−3.
Cho cấp số nhân (un) có u1 = 1; q = 2. Hỏi số 1024 là số hạng thứ mấy?
11.
9.
8.
10.
Tìm số hạng đầu u1 và công bội q của cấp số nhân biết \(\left\{ {\begin{array}{*{20}{c}}{{u_6} = 192}\\{{u_7} = 384}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{c}}{{{\rm{u}}_{\rm{1}}}{\rm{ = 5}}}\\{{\rm{q = 2}}}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{c}}{{{\rm{u}}_{\rm{1}}}{\rm{ = 6}}}\\{{\rm{q = 2}}}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{c}}{{{\rm{u}}_{\rm{1}}}{\rm{ = 9}}}\\{{\rm{q = 2}}}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{c}}{{{\rm{u}}_{\rm{1}}}{\rm{ = 9}}}\\{{\rm{q = 3}}}\end{array}} \right.\).
Cho một cấp số nhân có số hạng thứ 4 gấp 4096 lần số hạng đầu tiên. Tổng hai số hạng đầu tiên là 34. Số hạng thứ 3 của dãy số có giá trị bằng
1.
512.
1024.
32.
Cho cấp số nhân (un) có u1 = −3 và q = −2. Tính tổng 10 số hạng đầu tiên của cấp số nhân.
S10 = −511.
S10 = 1023.
S10 = 1025.
S10 = −1025.
Cho dãy (un) với \({u_n} = {\left( {\frac{1}{2}} \right)^n} + 1,\forall n \in {\mathbb{N}^*}\). Tính S2019 = u1 + u2 + u3 + … + u2019, ta được kết quả
\(2020 - \frac{1}{{{2^{2019}}}}\).
\(\frac{{4039}}{2}\).
\(2019 + \frac{1}{{{2^{2019}}}}\).
\(\frac{{6057}}{2}\).
Gọi S = 9 + 99 + 999 + ... + 999...9 (n số 9) thì S nhận giá trị nào sau đây?
\[\frac{{{{10}^{\rm{n}}} - 1}}{9}\].
\[10\left( {\frac{{{{10}^{\rm{n}}} - 1}}{9}} \right)\].
\[\left[ {10\left( {\frac{{{{10}^{\rm{n}}} - 1}}{9}} \right) - {\rm{n}}} \right]\].
\[10\left( {\frac{{{{10}^{\rm{n}}} - 1}}{9}} \right) + n\].
Người ta thiết kế một cái tháp 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là 12288 m2). tính diện tích của mặt trên cùng
6 m2.
8 m2.
10 m2.
12 m2.
Người ta nghiên cứu sự sinh sản của một loại vi rút trong 10 ngày nhận thấy quy luật: Ngày thứ nhất có 10 con; ngày thứ hai có 20 con; Ngày thứ ba có 40 con; … Cứ như thế, số con vi rút ở ngày sau nhiều gấp đôi số con vi rút ở ngày trước. Hỏi tổng số con vi rút đã có trong 10 ngày đó bằng bao nhiêu?
140.
10240.
1024.
10230.
Tế bào E.Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại nhân đôi một lần. Nếu lúc đầu có 1012 tế bào thì sau 3 giờ sẽ phân chia thành bao nhiêu tế bào?
1024.1012 tế bào.
256.1012 tế bào.
512.1012 tế bào.
512.1013 tế bào.
PHẦN II. TRẮC NGHIỆ4M ĐÚNG SAI
Cho cấp số nhân (un) có u1 = 2; u2 = −4.
a) Công bội q = 2.
b) u5 = −32.
c) Số −64 là số hạng thứ 6 của (un).
d) Tổng của 8 số hạng đầu tiên của cấp số nhân bằng −170.
Cho cấp số nhân (un) với công bội q < 0 và u2 = 4; u4 = 9.
a) Số hạng đầu \({u_1} = - \frac{8}{3}\).
b) Cấp số nhân có công bội \(q = - \frac{3}{2}\).
c) Số hạng \({u_5} = \frac{{27}}{2}\).
d) \( - \frac{{2187}}{{32}}\) là số hạng thứ 8.
Trong một hồ sen, số lá sen ngày hôm sau bằng 3 lần số lá sen ngày hôm trước. Biết rằng ngày đầu có 1 lá sen thì tới ngày thứ 10 hồ sen đầy lá sen.
a) u1 = 1.
b) Số lá sen lập thành cấp số nhân (un) với u1 = 1 và công bội q = 3.
c) Số lá sen lập thành cấp số cộng (un) với u1 = 1 và công sai d = 3.
d) Nếu ngày đầu có 9 lá sen thì tới ngày thứ 9 hồ sẽ đầy lá sen.
Cho cấp số nhân (un) có tổng n số hạng đầu tiên là Sn = 5n – 1.
a) Công bội của cấp số nhân đã cho là q = 6.
b) Số hạng đầu của cấp số nhân đã cho là u1 = 4.
c) Tổng 5 số hạng đầu của cấp số nhân là 3124.
d) Số hạng thứ 5 của cấp số nhân là 2600.
Cho tứ giác ABCD có bốn góc tạo thành một cấp số nhân có công bội bằng 2.
a) Số đo góc nhỏ nhất bằng 24°.
b) Số đo góc lớn nhất bằng 196°.
c) Tổng số đo góc lớn nhất với góc nhỏ nhất bằng 220°.
d) Số đo góc lớn nhất trừ cho số đo góc nhỏ nhất bằng 168°.
PHẦN III. TRẢ LỜI NGẮN
Ba số phân biệt có tổng bằng 146 có thể xem là ba số hạng đầu của một cấp số nhân hoặc có thể xem là số hạng thứ hai, số hạng thứ tư và số hạng thứ 20 của một cấp số cộng. Hãy tìm số lớn nhất trong ba số đó.
Viết thêm bốn số vào giữa hai số 160 và 5 để được một cấp số nhân gồm 6 số hạng. Tìm tổng tất cả các số hạng của cấp số nhân đó.
Cho x, y là các số nguyên thỏa mãn: Các số x + y; 2x + 3y; 9x + y theo thứ tự lập thành một cấp số cộng, đồng thời các số x – 1; y – 1; 2y – 2 theo thứ tự lập thành cấp số nhân. Tính tổng T = x + y.
Do ảnh hưởng của dịch Covid 19 nên doanh thu 6 tháng đầu năm của công ty A không đạt kế hoạch. Cụ thể, doanh thu 6 tháng đầu năm đạt 20 tỷ đồng, trong đó tháng 6 đạt 6 tỷ đồng. Để đảm bảo doanh thu cuối năm đạt được kế hoạch năm, công ty đưa ra chỉ tiêu: kể từ tháng 7 mỗi tháng phải tăng doanh thu so với tháng kề trước 10%. Hỏi theo chỉ tiêu đề ra thì doanh thu cả năm của công ty A đạt được là bao nhiêu tỷ đồng (làm tròn đến một chữ số thập phân).
Cho hình vuông ABCD có cạnh bằng 16 và có diện tích S1. Nối 4 trung điểm A1; B1; C1; D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2. Tiếp tục làm như thế, ta được hình vuông thứ ba là A2B2C2D2 có diện tích S3, … và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích S4, S5, …, S100 (tham khảo hình bên dưới).
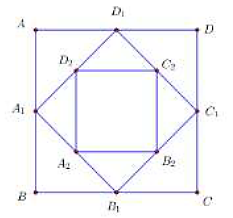
Biết tổng S = S1 + S2 + …+ S100 = \(\frac{{{2^a} - 1}}{{{2^b}}}\) (a, b Î ℕ). Tính a + b.








