26 câu hỏi
Giá trị lớn nhất của hàm số f(x) = trên đoạn là
-4
-2
-5
Cho hàm số f(x) có đồ thị của hàm số f'(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) = f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là
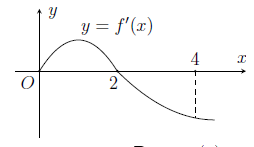
m = f(4), M = f(1)
m = f(4), M = f(2)
m = f(1), M = f(2)
m = f(0), M = f(2)
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) cho như hình vẽ.
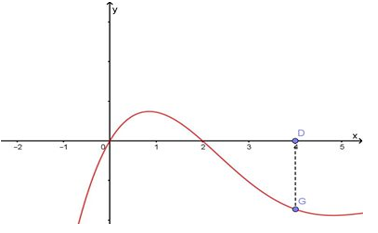
Biết rằng f(2) + f(4) = f(3) + f(0). Giá trị nhỏ nhất và lớn nhất của f(x) trên đoạn [0;4] lần lượt là
f(2), f(0)
f(4), f(2)
f(0), f(2)
f(2), f(4)
Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số g(x) = f() + trên đoạn [1;3].
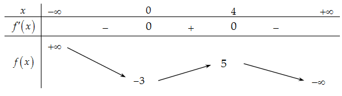
15
12
Có bao nhiêu số nguyên m để giá trị nhỏ nhất của hàm số y = || trên đoạn [0;2] đạt giá trị nhỏ nhất.
26
13
14
27
Xét hàm số f(x) = ||, với a,b là tham số. Gọi M là giá trị lớn nhất của hàm số trên [-1;3]. Khi M nhận giá trị nhỏ nhất có thể được, tính a + 2b.
2
4
-4
3
Cho hàm số y = . Tổng tất cả các giá trị thực tham số m sao cho bằng
-8
Biết rằng giá trị lớn nhất của hàm số y = || trên đoạn [0;2] đạt giá trị nhỏ nhất. Khi đó giá trị của tham số m bằng
-12
-13
-14
-11
Cho hàm số y = f(x) liên tục trên sao cho = f(2) = 4. Xét hàm số g(x) = . Giá trị của tham số m để là
5
4
-1
3
Gọi S là tập hợp các giá trị của tham số m để giá trị lớn nhất của hàm số y = trên đoạn [-1;1] bằng 3. Tính tổng tất cả các phần tử của S.
5
-1
Cho hàm số y = f(x) xác định trên tập số thực và có đạo hàm f'(x). Đồ thị hàm số y = f'(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) = f(4). - f(3). Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [0;4] là
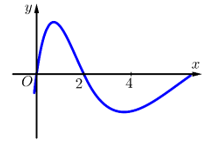
f(1)
f(0)
f(2)
f(4)
Kí hiệu m và M lần lượt là giá trị lớn nhất giá trị nhỏ nhất của hàm số y = trên đoạn [0;3]. Tính giá trị của tỉ số
Kết luận nào sau đây là đúng về giá trị lớn nhất và nhỏ nhất của hàm số y = ?
Hàm số có giá trị lớn nhất và giá trị nhỏ nhất.
Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất.
Hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất.
Hàm số có giá trị nhỏ nhất và không có giá trị lớn nhất.
Cho hàm số y = f(x) có đồ thị f'(x) như hình vẽ
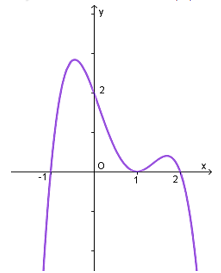
Giá trị lớn nhất của hàm số g(x) = f(x) - trên đoạn [-1;2] bằng
f(-1) -
f(1) -
f(2) -
-
Cho hàm số f(x) liên tục trên (0;+) thỏa mãn 3x.f(x) - , với f(x) 0, (0;+) và f(1) = . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Tính M + m.
Cho hàm số y = f(x) có đạo hàm f'(x). Hàm số y = f'(x) liên tục trên tập số thực và có bảng biến thiên như sau:
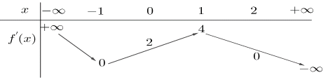
Biết rằng f(-1) = , f(2) = 6. Giá trị nhỏ nhất của hàm số g(x) = trên đoạn [-1;2] bằng
198
Cho hàm số f(x) = ||. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc đoạn [-3;2] sao cho M2m?
7
5
6
4
Gọi S là tập hợp giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số y = || trên đoạn [0;2] bằng 3. Số phần tử của S là:
0
2
3
1
Cho hàm số y = f(x) nghịch biến trên và thỏa mãn [f(x) - x]f(x) = . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng
4
-28
-3
33
Cho hàm số y = f(x). Đồ thị hàm số đạo hàm y = f'(x) như hình vẽ dưới đây. Xét hàm số g(x) = f(x) - . Mệnh đề nào dưới đây đúng?
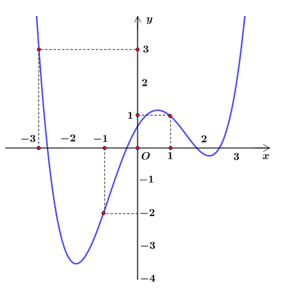
g(1)
g(-3)
g(-1)
Cho hàm số y = f(x) có bảng biến thiên như sau
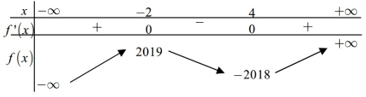
Tìm giá trị lớn nhất của hàm số g(x) = trên đoạn [-1;2]?
2022
2019
2020
2021
Cho hàm số f(x). Biết hàm số y = f'(x) có đồ thị như hình bên. Trên đoạn [-4;3], hàm số g(x) = 2f(x) + đạt giá trị nhỏ nhất tại điểm
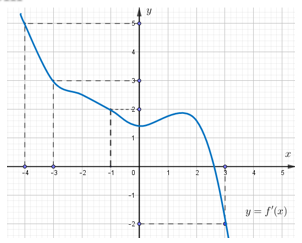
= -4
= -1
= 3
= -3
Tìm tất cả các số thực m để giá trị nhỏ nhất của hàm số y = 2 - 2msinx - (m+1)cosx bằng -3.
m = 2
m =
m =
m = 2, m =
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0;] là
1
2
Bất phương trình có nghiệm thuộc đoạn [1;9] khi và chỉ khi
m 5
m 6
m 5
m 6
Bất phương trình 3x + 1 m(x-2) nghiệm đúng với mọi x [3;5] khi và chỉ khi
m
m
m
m








