30 câu hỏi
Giá trị nhỏ nhất của hàm số f(x) = x + - 1 trên đoạn [-2;-1] bằng
-5
-6
-3
-4
Ký hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = trên đoạn [0;2]. Giá trị của a+A bằng
7
12
Tìm giá trị lớn nhất của hàm số f(x) = trên [-2;2].
5
17
15
-12
Tích giá trị lớn nhất và giái trị nhỏ nhất của hàm số y = trên đoạn bằng:
15
8
Cho hàm số y = f(x) liên tục trên đoạn [-2;6] và có đồ thị như hình vẽ bên dưới.

Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [-2;6]. Giá trị của M - m bằng
9
-8
-9
8
Bất phương trình m có nghiệm thuộc đoạn [1;2] khi và chỉ khi
m
m
m
m
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên đoạn . Khi đó giá trị của là
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = lần lượt là M và m. Chọn câu trả lời đúng.
M = 4, m = 2
M = 2, m = 0
M = 3, m = 2
M = 2, m =
Tìm giá trị của tham số thực m để giá trị nhỏ nhất của hàm số y = trên đoạn [0;4] bằng 3.
m = 3
m = 1
m = 7
m = 5
Cho hàm số y = f(x) xác định và liên tục trên R có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số. Giá trị của M – m bằng
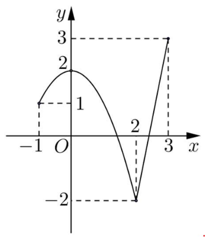
0.
1.
4.
5.
Gọi m, M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số f(x) = 2x + trên đoạn [-2;2]. Giá trị của m + M bằng
2
-2
0
-4
Giá trị nhỏ nhất của hàm số y = trên [-2;0] bằng :
-1
0
Tìm x để hàm số y = x + đạt giá trị lớn nhất
x = -2
x = 2
1
x =
Giá trị lớn nhất M của hàm số y = x + trên đoạn [0;4]
M = 4
M =
M = 3
M = 6
Gọi T là giá trị lớn nhất của hàm số y = trên đoạn [-1;2]. Tính giá trị T.
T = 4
T = -1
T = 20
T = 6
Giá trị nhỏ nhất m của hàm số y = trên đoạn [0;2] là:
m = -2
m = 0
m = -3
m = 11
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = (x-6) trên đoạn [0;3] có dạng a - b với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b + c.
4
-2
-22
5
Cho hàm số f(x) = - 3sinx + 2. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho. Khi đó M + 2m là
0
1
4
5
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x - . Tính tổng M + m.
M + m = 2 -
M + m = 2(1 + )
M + m = 2(1 - )
M + m = 4
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) = trên đoạn [-1;1]. Tính M + m.
-4
4
-2
2
Tìm giá trị nhỏ nhất của hàm số y = x + trên đoạn [2;4].
=
=
= 6
= -6
Cho hàm số y = f(x) có đạo hàm f'(x) = x(x+1) với mọi x. Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [-1;2] là
f(-1)
f(0)
f(3)
f(2)
Cho hàm số y = f(x) có đạo hàm f'(x) = với mọi . Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [-4;2] là
f(0)
f(-4)
f(1)
f(2)
Cho hàm số y = f(x) có đồ thị của đạo hàm f'(x) như hình vẽ bên dưới. Giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;3] là
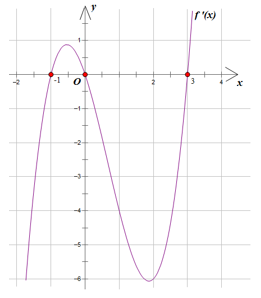
f(0)
f(-4)
f(1)
f(2)
Cho hàm số f(x) có đạo hàm f'(x) = -x. Giá trị lớn nhất của hàm số đã cho trên đoạn [0;4] bằng
f(0)
f(2)
f(3)
f(4)
Giá trị lớn nhất của hàm số y = 4 trên đoạn [-1;2] bằng
1
3
Không tồn tại
Giá trị lớn nhất của hàm số y = trên đoạn [-1;1] là:
2
0
-2
4
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số f(x) = trên đoạn [0;3]. Tính tổng S = 2m + 3M
S =
S =
S = -3
S = 4
Kí hiệu m và M lần lượt là giá trị lớn nhất giá trị nhỏ nhất của hàm số y = x + . Khi đó
M - m = 2 - 2
M - m = 4
M - m = 2 + 2
M - m = 2
Gọi M, m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số y = . Khi đó ta có
9M + m = 0
9M - m = 0
M + 9m = 0
M + m = 0








