22 câu Dạng 4. Tính tuần hoàn và chu kỳ hàm lượng giác
22 câu hỏi
Tìm chu kì cơ sở của hàm số y=2sin2x+3cos3x .
Xét tính tuần hoàn và tìm chu kì của hàm số
.
Chu kì của hàm số là
.
.
.
.
Đồ thị trong hình vẽ dưới đây là của hàm số nào?
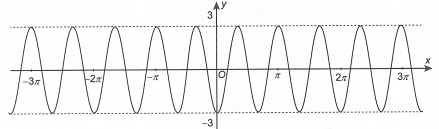
.
.
.
.
Hàm số là hàm số tuần hoàn với chu kì
.
T=6.
.
Khẳng định nào sau đây sai về hàm số y=2+sinx ?
Đồ thị hàm số không đi qua gốc tọa độ
Đồ thị hàm số nằm ở phía trên trục hoành.
Giá trị cực đại của y là 2.
Giá trị cực tiểu của y là 1.
Nếu chu kì tuần hoàn của hàm số là 4 thì
.
a=2.
Hàm số tuần hoàn với chu kì
.
.
Hàm số không có chu kì
Khẳng định nào sau đây đúng với hàm số ?
Biên độ là 2, chu kì là .
Biên độ là -2, chu kì là .
Biên độ là 2, chu kì là .
Biên độ là 2, chu kì là
Đồ thị trong hình vẽ dưới đây là của hàm số nào?
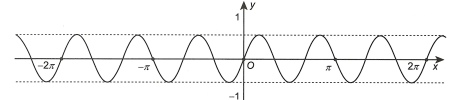
.
.
.
.
Chu kì của hàm số sau y=sin3x+2cos2x là
.
.
.
.
Với thì hàm số có giá trị cực đại là
0.
1.
.
Hàm số tuần hoàn có chu kì khi
.
.
.
.
Xét đồ thị hàm số với . Khẳng định nào sau đây đúng?
Đồ thị hàm số có một cực đại tại .
Đồ thị hàm số có một cực tiểu tại .
Đồ thị hàm số có một cực tiểu tại .
Hàm số đồng biến trên .
Đồ thị trong hình vẽ dưới đây là của hàm số nào?
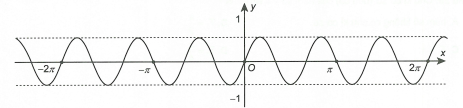
.
.
.
.
Chu kì của hàm số y=sin2x+sinx là
.
.
.
.
Chọn mệnh đề đúng trong các mệnh đề sau
Hàm số đồng biến trên khoảng .
Hàm số nghịch biến trên khoảng .
Hàm số đồng biến trên và nghịch biến trên khoảng .
Hàm số và cùng đồng biến trên khoảng .
Chu kì của hàm số y=tanx+tan3x là
.
.
.
.
Khẳng định nào sau đây đúng về hàm số ?
Chu kì , biên độ 2.
Chu kì , biên độ 2.
Chu kì , biên độ 1.
Chu kì , biên độ 1.
Chu kì của hàm số y=sin3x+2017cos2x là
.
.
.
.
Hình vẽ sau là đồ thị của hàm số . Biết và b nhỏ nhất, giá trị của biểu thức a+b là
0
1.
2.
3.
Chu kì cơ sở (nếu có) của hàm số là
hàm số không có chu kì cơ sở.
.
.
.