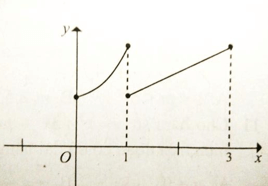21 câu hỏi
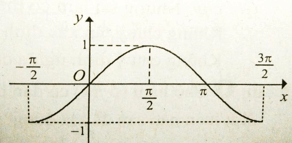
Cho đồ thị hàm số y = sin x với như hình vẽ.
Tìm khoảng đồng biến của hàm số y = sin x với
(-1;1)
Cho đồ thị hàm số như hình vẽ. Hàm số nghịch biến trên khoảng:
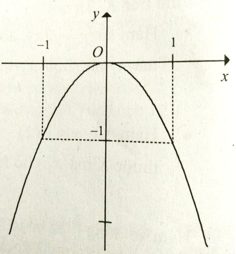
(-1;0)
(-∞;0)
(0;+∞)
(-1;1)
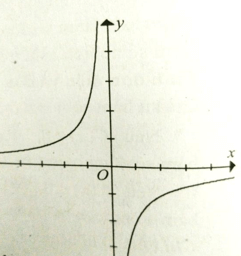
Cho đồ thị hàm số như hình vẽ. Hàm số đồng biến trên
(-∞;0)
(-∞;0) ∪ (0;+∞)
R
(-∞;0) và (0;+∞)
Cho hàm số f(x) có đạo hàm
Kết luận nào sau đây là đúng?
Hàm số f(x) nghịch biến trên khoảng (-∞;1).
Hàm số f(x) đồng biến trên các khoảng (-∞;0) và (1;+∞).
Hàm số f(x) đồng biến trên các khoảng và (1;+∞).
Hàm số f(x) đồng biến trên các khoảng (1;+∞).
Khoảng nghịch biến của hàm số là:
(1;3)
(-∞; 1) ∪ (3; +∞)
(-∞; 1) và (3; +∞)
(1;+∞)
Cho hàm số . Kết luận nào sau đây đúng?
Hàm số nghịch biến trên khoảng (-∞; -1) ∩ (0; 1)
Hàm số đồng biến trên khoảng (-1; 0) ∪ (1; +∞)
Hàm số nghịch biến trên khoảng (-∞; -1) ∪ (0; 1)
Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞)
Cho hàm số y = sin2x - 2x. Hàm số này
Luôn đồng biến trên R
Chỉ đồng biến trên khoảng (0; +∞)
Chỉ nghịch biến trên (-∞; -1)
Luôn nghịch biến trên R
Trong các hàm số sau, hàm số nào chỉ đồng biến trên khoảng (-∞; 1) ?
Tìm m để hàm số luôn nghịch biến trên khoảng xác định.
-2 < m ≤ 2
m < -2 hoặc m > 2
-2 < m < 2
m ≠ ±2
Cho hàm số , tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
m < 1
m ≥ 1
m ≤ -1
m ≥ -1
Cho đồ thị hàm số có dạng như hình vẽ.
Hàm số đồng biến trên:
(0;1)
(1;3)
(0;1) (1;3)
(0;1) và (1;3)
Hỏi hàm số đồng biến trên khoảng nào?
(-∞ ; +∞)
(-∞; -5)
(-5; +∞) ∪ (1; 3)
(0; 1) và (1; 3)
Tìm khoảng đồng biến của hàm số
(-∞; 1) ∪ (2; +∞)
(-∞; 1] và [2; +∞)
(-∞; 1) và (2; +∞)
(1;2)
Khoảng nghịch biến của hàm số là:
(-∞; -1) và (0; 1)
(-∞; 0) và (1; +∞)
(-∞; -1) ∪ (0; 1)
(0;1)
Cho hàm số
Khẳng định nào sau đây là khẳng định đúng?
Hàm số (1) nghịch biến trên R\{1}
Hàm số (1) nghịch biến trên (-∞; 1) và (1; +∞)
Hàm số (1) nghịch biến trên (-∞; 1) ∪ (1; +∞)
Hàm số (1) đồng biến trên (-∞; 1) và (1; +∞)
Tìm khoảng đồng biến của hàm số
R\{0}
(-∞; +∞)
(-1; 1)
(0; π)
Hàm số đồng biến trên khoảng nào?
R
(-∞; 0)
(-1; 0)
(0; +∞)
Cho hàm số Tìm điều kiện của tham số m để hàm số đồng biến trên R
m ≤ 2
m > 2
m ≥ 2
m <2
Cho hàm số
Tìm giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1).
Tìm tất cả các giá trị của tham số m sao cho hàm số nghịch biến trên
1 < m < 5
m ≥ 5
m < -1 hoặc m > 5
m > 5
Cho hàm số Tìm các giá trị của m để hàm số đồng biến trên đoạn có độ dài bằng 1.
m = 0
m = 1/4
m = 9/4
Không tồn tại