Trắc nghiệm Toán 12: Chủ đề 8. Dạng lượng giác số phức có đáp án
34 câu hỏi
Viết các số phức sau dưới dạng lượng giác:
a) ![]() b)
b) ![]()
c) ![]() d)
d) 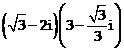
Viết các số phức sau dưới dạng lượng giác:
a) ![]() ; b)
; b) ![]() ;
;
c) ![]() d)
d) ![]()
Viết các số phức sau dưới dạng lượng giác![]()
Viết các số phức sau dưới dạng lượng giác:![]()
Viết dưới dạng lượng giác các số phức sau:![]()
Tính các giá trị của số phức sau và viết kết quả của chúng dưới dạng ![]() ;b)
;b) 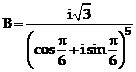 ;
;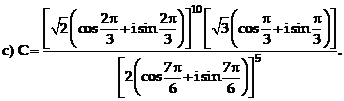
Cho số phức ![]() . Tìm m nguyên để z là số thực, z là số ảo
. Tìm m nguyên để z là số thực, z là số ảo
Cho số phức . Tính z7.
Cho số phức z thỏa mãn: ![]() . Tìm phần thực của số phức z2013.
. Tìm phần thực của số phức z2013.
Gọi z1, z2 là hai nghiệm phức của phương trình ![]() . Tìm phần thực, phần ảo của số phức
. Tìm phần thực, phần ảo của số phức ![]() .
.
Cho các số phức z thỏa mãn: ![]() . Chứng minh rằng z có phần thực bằng 1.
. Chứng minh rằng z có phần thực bằng 1.
Biết rằng số phức z thỏa mãn ![]() . Hãy tính
. Hãy tính ![]()
Cho ![]() Tính
Tính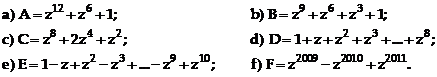
Chứng minh rằng:
a) ![]() và
và ![]()
b) Cho số phức ![]() .Tính
.Tính ![]()
Tìm phần thực của số phức ![]() . Trong đó n thỏa mãn:
. Trong đó n thỏa mãn: ![]() .
.
Cho số phức ![]() . Viết z dưới dạng lượng giác. Tìm phần thực và phần ảo của số phức
. Viết z dưới dạng lượng giác. Tìm phần thực và phần ảo của số phức ![]() .
.
Tìm điều kiện đối với các số phức a,b,c sao cho với mọi số phức z thỏa mãn thì ![]() là số thực.
là số thực.
Tính môđun và một acgumen của số phức sau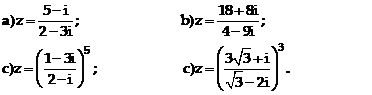
Cho số phức z thỏa mãn ![]() . Tìm mô-đun của số phức
. Tìm mô-đun của số phức ![]() .
.
Tìm số phức z biết rằng ![]() và
và 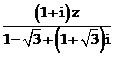 có một acgumen bằng
có một acgumen bằng
Viết dạng lượng giác của số phức z biết ![]() và có một acgumen bằng .
và có một acgumen bằng .
Tìm số phức z biết ![]() là số thực và
là số thực và ![]() có một acgumen là .
có một acgumen là .
Tìm số phức z sao cho ![]() có một acgumen bằng và
có một acgumen bằng và ![]()
Trong các số phức z thỏa mãn ![]() , số phức nào có nhỏ nhất. Khi đó acgumen của nó bằng bao nhiêu?
, số phức nào có nhỏ nhất. Khi đó acgumen của nó bằng bao nhiêu?
Tìm số phức z thỏa mãn ![]() và
và ![]() có một acgumen bằng .
có một acgumen bằng .
Xét số phức z thỏa điều kiện ![]()
a) Tìm tập hợp điểm M biểu diễn số phức z thỏa (*)
b) Trong các số phức z thỏa (*) tìm số số phức có acgumen dương và nhỏ nhất.
Tìm số phức z sao cho ![]() và z + 1 có một acgumen bằng .
và z + 1 có một acgumen bằng .
Xác định tập hợp các điểm trên mặt phẳng phức biểu diễn số phức z sao cho số phức có một acgument bằng
Tìm căn bậc hai của số phức sau và viết dưới dạng lượng giác ![]()
Tìm căn bậc ba của số phức sau và viết dưới dạng lượng giác ![]()
Tính căn bậc bốn của ![]()
Tính căn bậc năm của w = i
a) Viết ![]() dưới dạng lượng giác.
dưới dạng lượng giác.
b) Tính và suy ra các căn bậc bốn của ![]()








