25 câu hỏi
#2H3Y1-2~Trong không gian với hệ tọa độ số Oxyz cho các điểm A(1; 2; 3), B(2; 1; 5), C(2; 4; 2). Góc giữa hai đường thẳng AB và AC bằng:
600
300
1200
1500
Trong không gian với hệ tọa độ Oxyz cho là
Trong không gian Oxyz, cho đường thẳng d: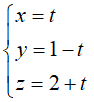
. Đường thẳng d đi qua điểm nào sau đây:
K(1;-1;1)
F(0;1;2)
E(1;1;2)
H(1;2;0).
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x² + y² + z² - 2x + 4y - 6z + 9 =0. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S).
I(-1;2;3),R=√5
I(1;-2;3),R=√5
I(1;-2;3),R=5
I(-1;2;-3),R=5.
Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu tâm K(0;2;2√2) và tiếp xúc với mặt phẳng (Oxy) là:
x2+(y-2)2+(z-2√2)2=4
x2+(y-2)2+(z-2√2)2=8
x2+(y-2)2+(z-2√2)2=2√2
x2+(y-2)2+(z-2√2)2=2.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) : x² + y² + z² - 2x + 4z + 1= 0. Tâm của mặt cầu là điểm:
I(1;-2;0)
I(1;0;-2)
I(-1;2;0)
I(0;1;2).
#2H3Y1-3~Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): (x+1)²+(y-2)²+(z-1)²=9. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S).
I(-1;2;1)vàR=3
I(-1;2;1)vàR=9
I(1;-2;-1)vàR=3
I(1;-2;-1)vàR=9.
#2H3Y1-3~Trong không gian Oxyz, phương trình mặt cầu (S) đường kính AB với A(4; -3; 5), B(2; 1; 3) là:
x²+y²+z²+6x+2y-8z-26=0
x²+y²+z²-6x+2y-8z+20=0
x²+y²+z²+6x-2y+8z-20=0
x²+y²+z²-6x+2y-8z+26=0.
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz. Tìm tâm I và tính bán kính R của mặt cầu (S): x²+y²+z²-2x-4y+2z+2=0.
I(-1;-2;1),R=2
I(1;2;-1),R=2√2
I(-1;-2;1),R=2√2
I(1;2;-1),R=2.
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-5)² + (y-1)² + (z+2)²=9. Tính bán kính R của mặt cầu (S).
R=18
R=9
R=3
R=6.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²+2x-4y+6z-2=0. Tìm tọa độ tâm I và tính bán kính R của (S).
TâmI(-1;2;-3)vàbánkínhR=4
TâmI(1;-2;3)vàbánkínhR=4
TâmI(-1;2;3)vàbánkínhR=4
TâmI(1;-2;3)vàbánkínhR=16.
#2H3Y1-3~Trong không gian tọa độ Oxyz, xác định phương trình mặt cầu có tâm I(3;-1;2) và tiếp xúc mặt phẳng (P): x+2y-2z=0.
(x-3)²+(y+1)²+(z-2)2=2
(x-3)²+(y+1)²+(z-2)²=1
(x+3)²+(y-1)²+(z+2)2=1
(x+3)²+(y-1)²+(z+2)²=4.
#2H3Y1-3~Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+(y+2)²+z²=25. Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
I(1;-2;0),R=5
I(-1;2;0),R=25
I(1;-2;0),R=25
I(-1;2;0),R=5.
Trong không gian Oxyz, phương trình mặt cầu tâm I(2;1;-3) bán kính R=4 là:
(x+2)²+(y+1)²+(z-3)²=16
(x+2)²+(y+1)²+(z-3)²=4
(x-2)²+(y-1)²+(z+3)²=4
(x-2)²+(y-1)²+(z+3)²=16.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình là x²+y²+z²-2x-4y-6z+5=0. Tính diện tích mặt cầu (S).
42π
36π
9π
12π.
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình (x+1)²+(y-3)²+z²=16. Tìm tọa độ tâm I và bán kính R của mặt cầu đó.
I(-1;3;0),R=4
I(1;-3;0),R=4
I(-1;3;0),R=16
I(1;-3;0),R=16.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ): ( x-5 )²+( y-1 )²+( z+2 )²=16. Tính bán kính của (S).
4
16
7
5.
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²-2x-4y-6z-11=0. Toạ độ tâm T của (S) là:
T(1;2;3)
T(2;4;6)
T(-2;-4;-6)
T(-1;-2;-3)
Trong không gian Oxyz, mặt cầu tâm I(1;2;3) đi qua điểm A(1;1;2) có phương trình là:
(x-1)²+(y-1)²+(z-2)²=2
(x-1)²+(y-2)²+(z-3)²=2
(x-1)²+(y-2)²+(z-3)²=√2
(x-1)²+(y-1)²+(z-2)²=√2.
Trong không gian với hệ trục tọa độ Oxyz, cho điểm I(1;0;-2) và mặt phẳng (P) có phương trình x + 2y -2z +4 =0. Phương trình mặt cầu (S) tâm I và tiếp xúc với mặt phẳng (P) là:
(x-1)²+y²+(z+2)²=9
(x-1)²+y²+(z+2)²=3
(x+1)²+y²+(z-2)²=3
(x+1)²+y²+(z-2)²=9.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x²+y²+z²-x+2y+1=0. Tìm tọa độ tâm I và bán kính R của (S).
I(-1/2;1;0)vàR= 1/4
I(1/2;1;0)vàR=1/2
I(1/2;-1;0)vàR=1/2
I(-1/2;1;0)vàR= 1/2
Trong không gian Oxyz, cho mặt cầu (S): x²+y²+z²-2x+6y-6=0. Bán kính của (S) bằng:
√46
16
2
4.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x-2y-2z+3=0. Tính khoảng cách d từ điểm M(2;1;0) đến mặt phẳng (P).
d = 1/3
d = √3/3
d = 3
d = 1
#2H3Y2-1~Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;3;2), B(2;-1;5) và C(3;2;-1). Gọi 
#$\overrightarrow{AB}$,$\overrightarrow{AC}$~ là tích có hướng của hai véc-tơ 
. Tìm tọa độ véc-tơ .
=(15;9;7)
=(9;3;-9).
=(3;-9;9)}
=(9;7;15)}
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P:3x-4y+5z-2=0. Véc-tơ nào dưới đây là một véc-tơ pháp tuyến của mặt phẳng P?
=(3;-5;-2)
=(-4;5;-2)
=(3;-4;5)
=(3;-4;2).
